23.1 图形的旋转(2)
文档属性
| 名称 | 23.1 图形的旋转(2) | 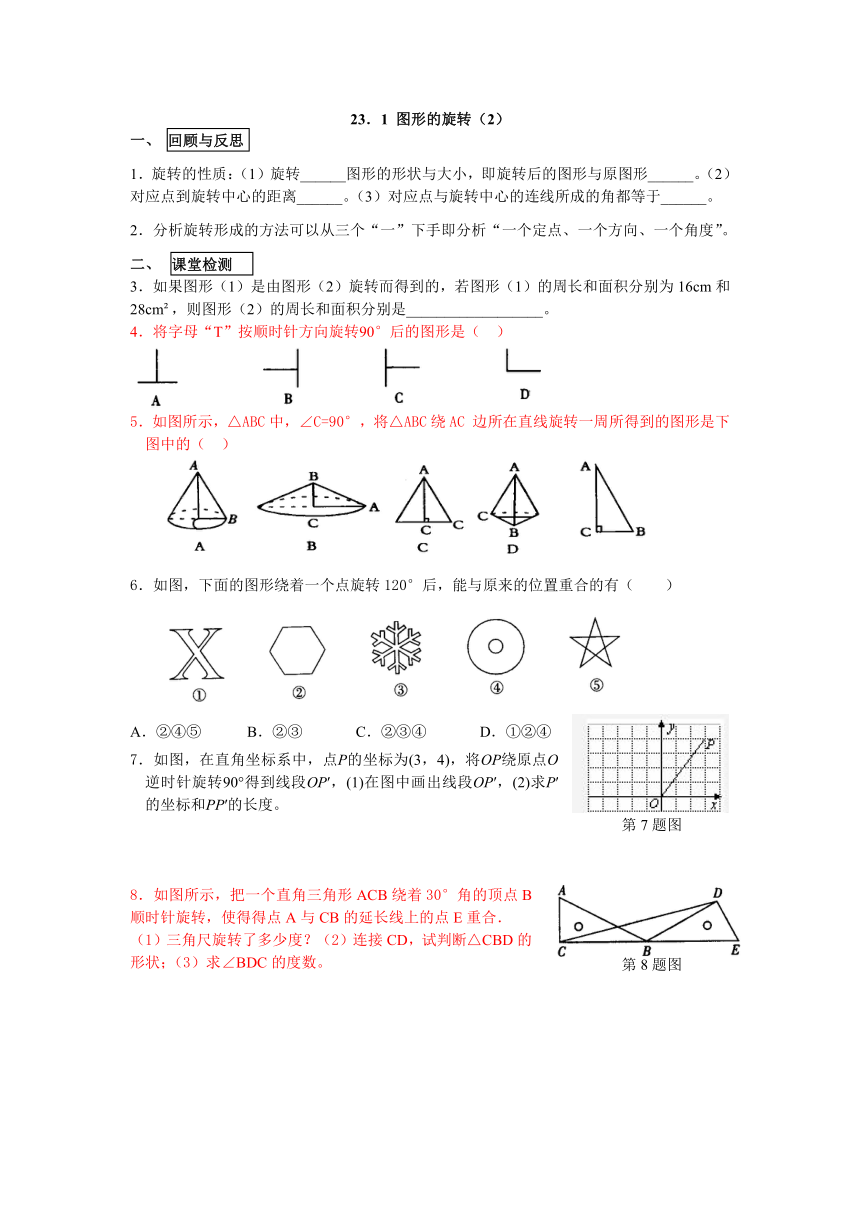 | |
| 格式 | rar | ||
| 文件大小 | 40.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-24 14:37:00 | ||
图片预览

文档简介
23.1 图形的旋转(2)
一、
1.旋转的性质:(1)旋转______图形的形状与大小,即旋转后的图形与原图形______。(2)对应点到旋转中心的距离______。(3)对应点与旋转中心的连线所成的角都等于______。
2.分析旋转形成的方法可以从三个“一”下手即分析“一个定点、一个方向、一个角度”。
二、
3.如果图形(1)是由图形(2)旋转而得到的,若图形(1)的周长和面积分别为16cm和28cm ,则图形(2)的周长和面积分别是__________________。
4.将字母“T”按顺时针方向旋转90°后的图形是( )
5.如图所示,△ABC中,∠C=90°,将△ABC绕AC边所在直线旋转一周所得到的图形是下图中的( )
6.如图,下面的图形绕着一个点旋转120°后,能与原来的位置重合的有( )
A.②④⑤ B.②③ C.②③④ D.①②④
7.如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′,(1)在图中画出线段OP′,(2)求P′的坐标和PP′的长度。
8.如图所示,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使得得点A与CB的延长线上的点E重合.
(1)三角尺旋转了多少度?(2)连接CD,试判断△CBD的形状;(3)求∠BDC的度数。
9.如图所示,△ABC是等腰直角三角形,∠C是直角,请在方格线中画出△ABC绕点A逆时针方向依次旋转45°、90°、135°后的图形.
10、奥运的标志“五环”若把它看作是一个圆改变旋转中心旋转后得到的,你想一想,它是经过几次旋转得到的?在下图中标出所有的旋转中心。
三、
11.如图,将边长为2cm的两个互相垂直的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为cm2,
则这个旋转角度为______度.
12.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上。
(1)如图1, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等。”是否正确,若正确请说明理由,若不正确请举反例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图2为例说明理由。
答案
1、⑴不改变,全等⑵相等⑶旋转角;3、16cm和28cm ;4、B;5、A;6、C;7、⑴略⑵⑶;8、⑴120°⑵等腰三角形⑶30°;9、略;10、4次,两圆圆心连线的中点;11、60°;12、⑴不相等,用图2即可说明;⑵BE=DG。理由:连接BE,在△ADG和△ABE中,∵AD=AB,∠∠DAG=∠BAE,AG=AE,∴ADG≌ABE(SAS),∴BE=DG。
课外拓展
第8题图
第7题图
课堂检测
回顾与反思
一、
1.旋转的性质:(1)旋转______图形的形状与大小,即旋转后的图形与原图形______。(2)对应点到旋转中心的距离______。(3)对应点与旋转中心的连线所成的角都等于______。
2.分析旋转形成的方法可以从三个“一”下手即分析“一个定点、一个方向、一个角度”。
二、
3.如果图形(1)是由图形(2)旋转而得到的,若图形(1)的周长和面积分别为16cm和28cm ,则图形(2)的周长和面积分别是__________________。
4.将字母“T”按顺时针方向旋转90°后的图形是( )
5.如图所示,△ABC中,∠C=90°,将△ABC绕AC边所在直线旋转一周所得到的图形是下图中的( )
6.如图,下面的图形绕着一个点旋转120°后,能与原来的位置重合的有( )
A.②④⑤ B.②③ C.②③④ D.①②④
7.如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′,(1)在图中画出线段OP′,(2)求P′的坐标和PP′的长度。
8.如图所示,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使得得点A与CB的延长线上的点E重合.
(1)三角尺旋转了多少度?(2)连接CD,试判断△CBD的形状;(3)求∠BDC的度数。
9.如图所示,△ABC是等腰直角三角形,∠C是直角,请在方格线中画出△ABC绕点A逆时针方向依次旋转45°、90°、135°后的图形.
10、奥运的标志“五环”若把它看作是一个圆改变旋转中心旋转后得到的,你想一想,它是经过几次旋转得到的?在下图中标出所有的旋转中心。
三、
11.如图,将边长为2cm的两个互相垂直的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为cm2,
则这个旋转角度为______度.
12.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上。
(1)如图1, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等。”是否正确,若正确请说明理由,若不正确请举反例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图2为例说明理由。
答案
1、⑴不改变,全等⑵相等⑶旋转角;3、16cm和28cm ;4、B;5、A;6、C;7、⑴略⑵⑶;8、⑴120°⑵等腰三角形⑶30°;9、略;10、4次,两圆圆心连线的中点;11、60°;12、⑴不相等,用图2即可说明;⑵BE=DG。理由:连接BE,在△ADG和△ABE中,∵AD=AB,∠∠DAG=∠BAE,AG=AE,∴ADG≌ABE(SAS),∴BE=DG。
课外拓展
第8题图
第7题图
课堂检测
回顾与反思
同课章节目录
