7.1两条直线的位置关系(第一课时) 学案
文档属性
| 名称 | 7.1两条直线的位置关系(第一课时) 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 25.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-07 11:53:36 | ||
图片预览

文档简介
六年级数学(下)导学案(第七章)
7.1两条直线的位置关系(第一课时)
【学习目标】
1.了解对顶角、补角、余角,知道对顶角相等、等角的余角相等、等角的补角相等,并能解决一些实际问题;
2.能运用互为余角、互为补角、对顶角等相关的知识解决一些实际问题。
【课前预习】
1.①什么是直角?②什么是平角?
2.①在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少
②已知∠1=36°,∠2=54°,那么∠1+∠2=_________
③已知∠1=144°,∠2=36°,那么∠1+∠2=_________
【课中探究】
一、展示新知:(认真阅读课本64、65页回答下列问题:)
1.(1)什么叫相交线?(2)什么叫平行线?(3)什么叫对顶角?(4)对顶角有什么性质?
2.(1)在一副三角尺中,每块都有一个角是90o,而其他两个角的和是90o 。一般情况下,如果两个角的和等于90o (直角),我们就说这两个角互为余角,即其中一个角是另一个角的余角.例如,∠1与∠2互为余角,∠1是∠2的余角,∠2也是∠1的余角.
同样,如果两个角的和等于180o (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
(2)符号语言:若∠1+∠2= 90o , 那么∠1与∠2互余。
(3)若∠3+∠4=180o , 那么∠3与∠4互补。
3.注:
(1)“互为”这个词语,与“互为相反数”、“互为倒数”等词语中的含义有联系,均表示成对出现;
(2)互为余角以及互为补角的角,主要反映了角的数量关系,而不是角的位置关系;
(3)区分互为补角和互为余角,区别在于两角的和是180°还是90°。
练一练
(1)若∠1与∠2互余,则∠1+∠2=__________
(2)若∠1= 90o—∠2,则∠1+∠2=__________
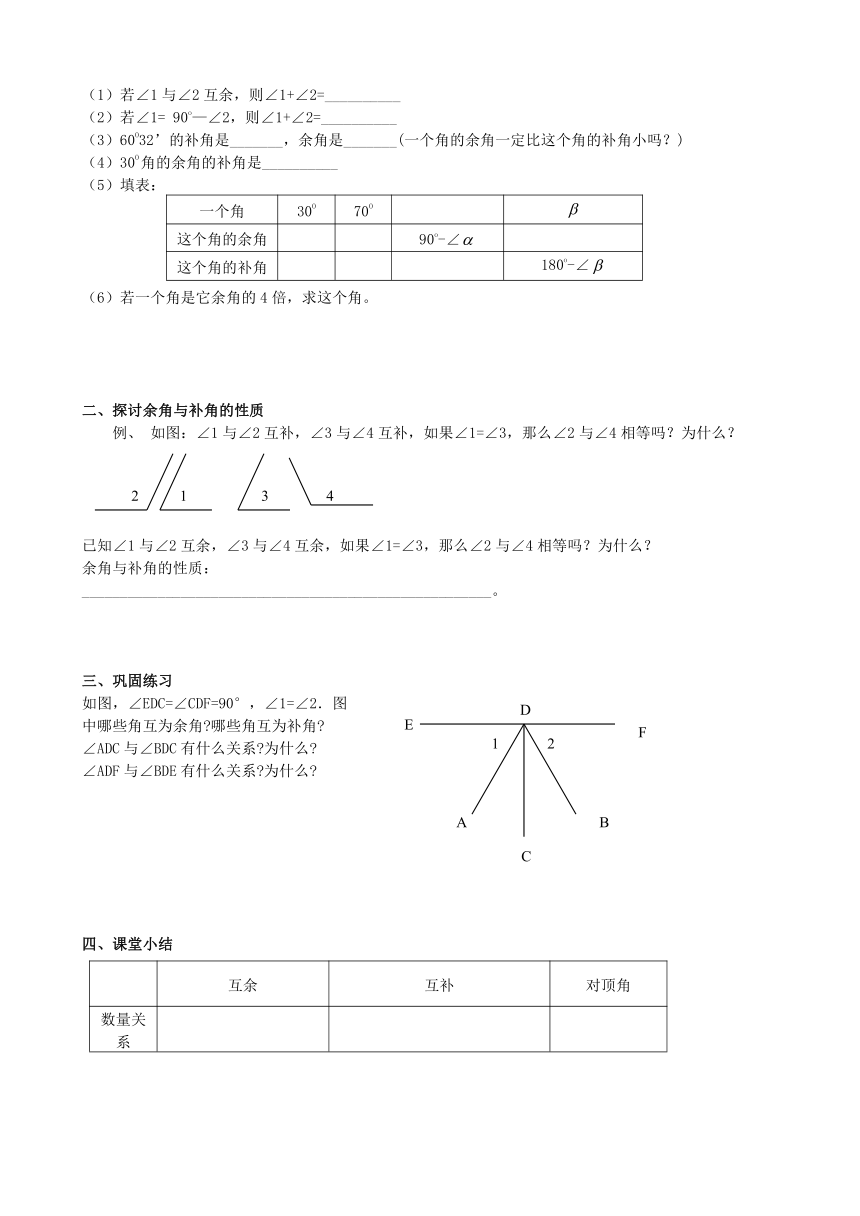
(3)60O32’的补角是_______,余角是_______(一个角的余角一定比这个角的补角小吗?)
(4)30O角的余角的补角是__________
(5)填表:
一个角 30O 70O
这个角的余角 90o-∠
这个角的补角 180o-∠
(6)若一个角是它余角的4倍,求这个角。
二、探讨余角与补角的性质
例、 如图:∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
HYPERLINK "http://www.21cnjy.com"
已知∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
余角与补角的性质:
______________________________________________________。
三、巩固练习
如图,∠EDC=∠CDF=90°,∠1=∠2.图
中哪些角互为余角 哪些角互为补角
∠ADC与∠BDC有什么关系 为什么
∠ADF与∠BDE有什么关系 为什么
四、课堂小结
互余 互补 对顶角
数量关系
对应图形关系
性质
【当堂达标】
1.已知∠A=40°,则∠A的余角等于______.
2.如图所示,直线AB,CD相交于点O,∠BOE=90°,若∠COE=55°,求∠BOD的度数.
3.如图所示,直线AB与CD相交于点O,OE平分∠AOD,∠AOC=120°。求∠BOD,
∠AOE的度数.
【课后巩固】
1.一个角的补角是它的3倍,求这个角。
2.一个角的补角是这个角的余角的4倍,求这个角。
3.如图所示,三条直线AB,CD,EF相交于点O,
∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数.
4.如图所示,当光线从空气射入水中时,光线的传播
方向发生了改变,这就是光的折射现象.若∠1=42°,
∠2=28°,则光的传播方向改变了______度.
1 ∠3与∠4
2
2
1
4
3
4
2
1
3
4
D
2
E
F
A
1
B
C
2
1
1 ∠3与∠4
2
4
3
4
7.1两条直线的位置关系(第一课时)
【学习目标】
1.了解对顶角、补角、余角,知道对顶角相等、等角的余角相等、等角的补角相等,并能解决一些实际问题;
2.能运用互为余角、互为补角、对顶角等相关的知识解决一些实际问题。
【课前预习】
1.①什么是直角?②什么是平角?
2.①在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少
②已知∠1=36°,∠2=54°,那么∠1+∠2=_________
③已知∠1=144°,∠2=36°,那么∠1+∠2=_________
【课中探究】
一、展示新知:(认真阅读课本64、65页回答下列问题:)
1.(1)什么叫相交线?(2)什么叫平行线?(3)什么叫对顶角?(4)对顶角有什么性质?
2.(1)在一副三角尺中,每块都有一个角是90o,而其他两个角的和是90o 。一般情况下,如果两个角的和等于90o (直角),我们就说这两个角互为余角,即其中一个角是另一个角的余角.例如,∠1与∠2互为余角,∠1是∠2的余角,∠2也是∠1的余角.
同样,如果两个角的和等于180o (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
(2)符号语言:若∠1+∠2= 90o , 那么∠1与∠2互余。
(3)若∠3+∠4=180o , 那么∠3与∠4互补。
3.注:
(1)“互为”这个词语,与“互为相反数”、“互为倒数”等词语中的含义有联系,均表示成对出现;
(2)互为余角以及互为补角的角,主要反映了角的数量关系,而不是角的位置关系;
(3)区分互为补角和互为余角,区别在于两角的和是180°还是90°。
练一练
(1)若∠1与∠2互余,则∠1+∠2=__________
(2)若∠1= 90o—∠2,则∠1+∠2=__________
(3)60O32’的补角是_______,余角是_______(一个角的余角一定比这个角的补角小吗?)
(4)30O角的余角的补角是__________
(5)填表:
一个角 30O 70O
这个角的余角 90o-∠
这个角的补角 180o-∠
(6)若一个角是它余角的4倍,求这个角。
二、探讨余角与补角的性质
例、 如图:∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
HYPERLINK "http://www.21cnjy.com"
已知∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
余角与补角的性质:
______________________________________________________。
三、巩固练习
如图,∠EDC=∠CDF=90°,∠1=∠2.图
中哪些角互为余角 哪些角互为补角
∠ADC与∠BDC有什么关系 为什么
∠ADF与∠BDE有什么关系 为什么
四、课堂小结
互余 互补 对顶角
数量关系
对应图形关系
性质
【当堂达标】
1.已知∠A=40°,则∠A的余角等于______.
2.如图所示,直线AB,CD相交于点O,∠BOE=90°,若∠COE=55°,求∠BOD的度数.
3.如图所示,直线AB与CD相交于点O,OE平分∠AOD,∠AOC=120°。求∠BOD,
∠AOE的度数.
【课后巩固】
1.一个角的补角是它的3倍,求这个角。
2.一个角的补角是这个角的余角的4倍,求这个角。
3.如图所示,三条直线AB,CD,EF相交于点O,
∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数.
4.如图所示,当光线从空气射入水中时,光线的传播
方向发生了改变,这就是光的折射现象.若∠1=42°,
∠2=28°,则光的传播方向改变了______度.
1 ∠3与∠4
2
2
1
4
3
4
2
1
3
4
D
2
E
F
A
1
B
C
2
1
1 ∠3与∠4
2
4
3
4
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
