2023—2024学年北师大版数学八年级上册 第四章一次函数 章节检测 (无答案)
文档属性
| 名称 | 2023—2024学年北师大版数学八年级上册 第四章一次函数 章节检测 (无答案) | 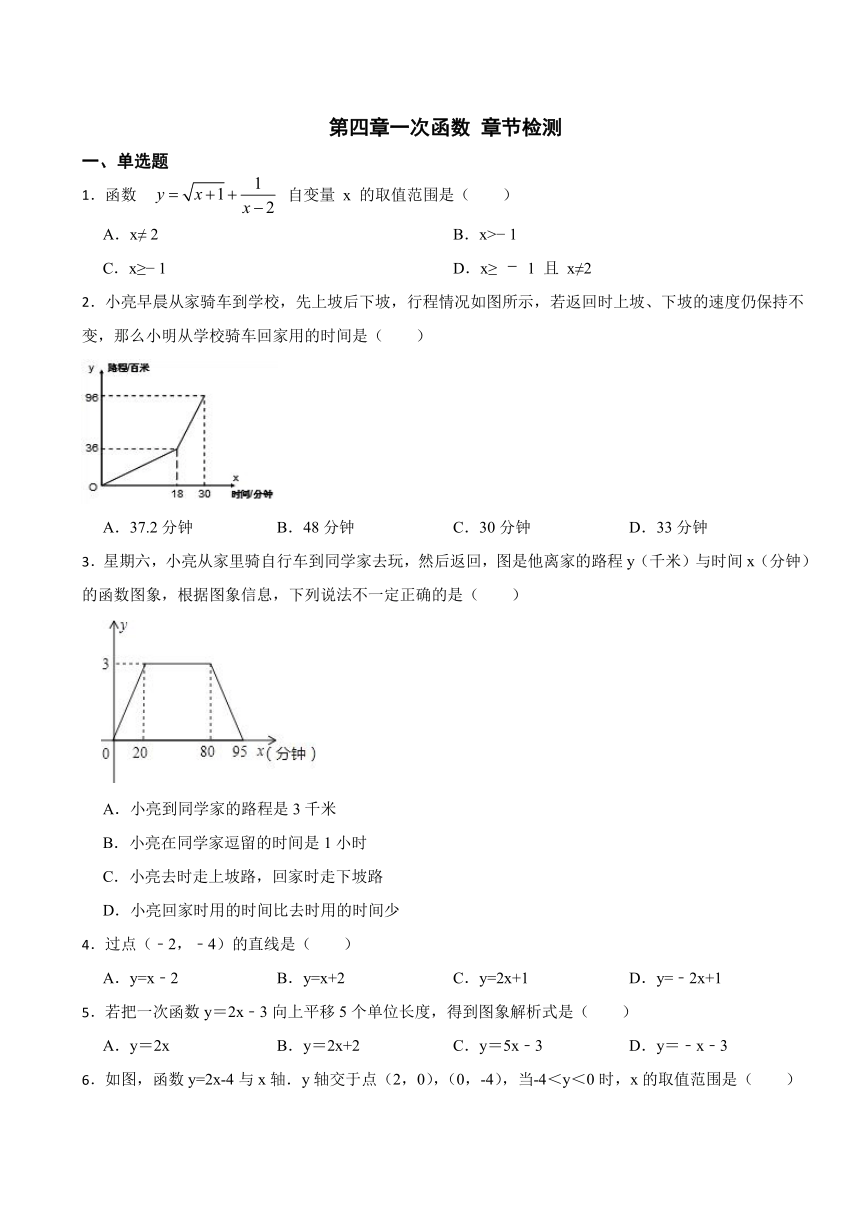 | |
| 格式 | docx | ||
| 文件大小 | 110.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 13:39:06 | ||
图片预览

文档简介
第四章一次函数 章节检测
一、单选题
1.函数 自变量 x 的取值范围是( )
A.x≠ 2 B.x> 1
C.x≥ 1 D.x≥ 1 且 x≠2
2.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
A.37.2分钟 B.48分钟 C.30分钟 D.33分钟
3.星期六,小亮从家里骑自行车到同学家去玩,然后返回,图是他离家的路程y(千米)与时间x(分钟)的函数图象,根据图象信息,下列说法不一定正确的是( )
A.小亮到同学家的路程是3千米
B.小亮在同学家逗留的时间是1小时
C.小亮去时走上坡路,回家时走下坡路
D.小亮回家时用的时间比去时用的时间少
4.过点(﹣2,﹣4)的直线是( )
A.y=x﹣2 B.y=x+2 C.y=2x+1 D.y=﹣2x+1
5.若把一次函数y=2x﹣3向上平移5个单位长度,得到图象解析式是( )
A.y=2x B.y=2x+2 C.y=5x﹣3 D.y=﹣x﹣3
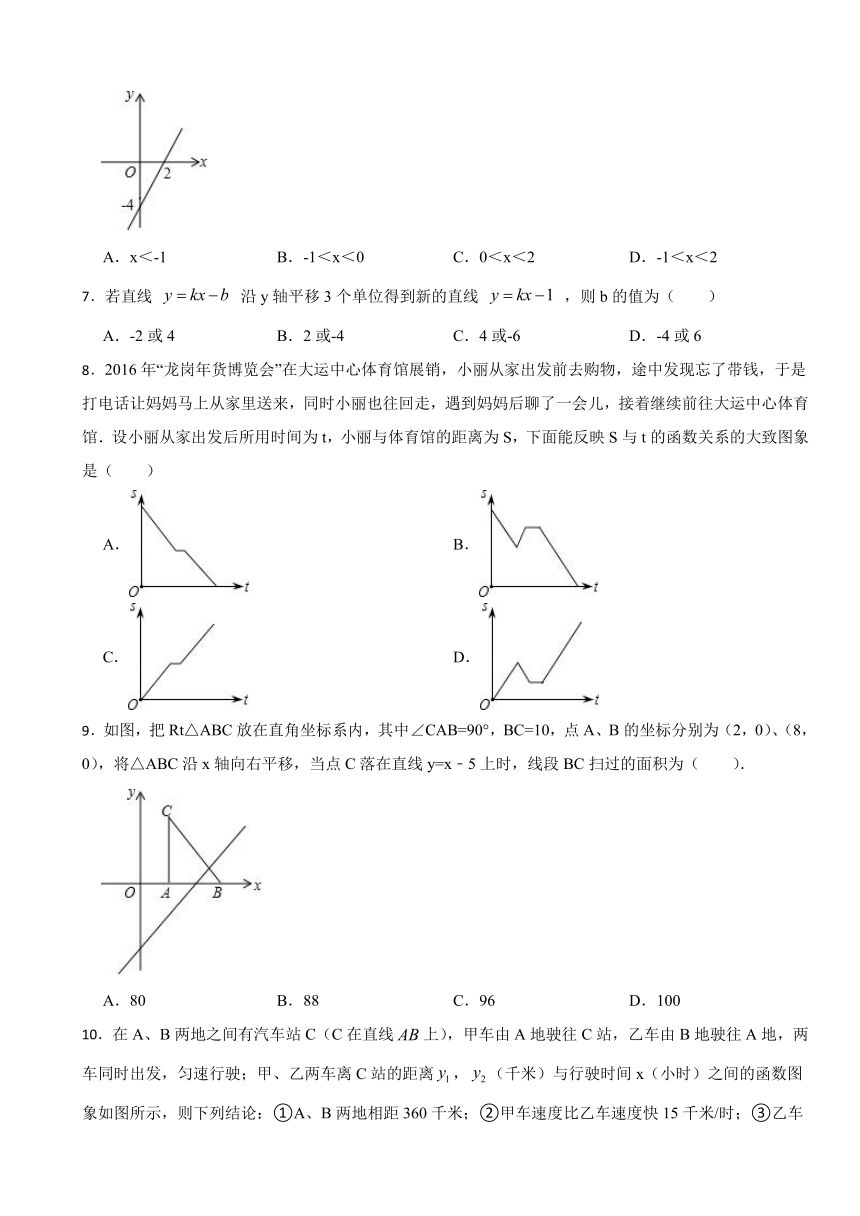
6.如图,函数y=2x-4与x轴.y轴交于点(2,0),(0,-4),当-4<y<0时,x的取值范围是( )
A.x<-1 B.-1<x<0 C.0<x<2 D.-1<x<2
7.若直线 沿y轴平移3个单位得到新的直线 ,则b的值为( )
A.-2或4 B.2或-4 C.4或-6 D.-4或6
8.2016年“龙岗年货博览会”在大运中心体育馆展销,小丽从家出发前去购物,途中发现忘了带钱,于是打电话让妈妈马上从家里送来,同时小丽也往回走,遇到妈妈后聊了一会儿,接着继续前往大运中心体育馆.设小丽从家出发后所用时间为t,小丽与体育馆的距离为S,下面能反映S与t的函数关系的大致图象是( )
A. B.
C. D.
9.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
10.在A、B两地之间有汽车站C(C在直线上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶;甲、乙两车离C站的距离,(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇;其中正确的结论有( )
A.1 B.2个 C.3个 D.4个
二、填空题
11.将一次函数y=﹣2x﹣1的图象沿y轴向上平移3个单位后,得到的图象对应的函数关系式为 .
12.如图所示,在三角形 中,已知 ,高 ,动点 由点 沿 向点 移动 不与点 重合 设 的长为 ,三角形 的面积为 ,则 与 之间的关系式为 .
13.如图,直线AB是一次函数y=kx+b的图像,若线段AB的长度为,则此函数的表达式为 .
14.某复印店用电脑编辑并打印一张文稿收费2元,再每复印一张收费0.3元,则总收费y(元)与同样文稿的数量x(张)之间的关系式是 .
15.已知直线y=﹣ 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为 个.
三、解答题
16.已知正比例函数y=(m+2)x中,y的值随x的增大而增大,而正比例函数y=(2m-3)x,y的值随x的增大而减小,且m为整数,你能求出吗?为什么?
17.若直线y=kx+b与直线y=2x+2 关于x轴对称,求y与x的函数关系式.
18.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(3)若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
19.在同一平面直角坐标系中,观察以下直线:y=2x,y=﹣x+6,y=x+2,y=4x﹣4图象的共同特点,若y=kx+5也有该特点,试求满足条件的k值.
20.某企业生产一种收音机,其成本24元.直接由厂家门市部销售,每台售价32元,门市部的销售需消耗费用每月2400元,如果委托商店销售,出厂价每台28元,销售多少台时两种销售方式所获得的利润相等?若销售量达每月2000台,问采用哪种销售方式,取得的利润较多?
21.如图,直线y=-x+6分别与x轴、y轴交于A、B两点;直线y=与AB交于点C,过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
(1)求点C的坐标;
(2)当0<x<5时,求S与t之间的函数关系式;
(3)求(2)中S的最大值.
22.台州市某体育用品商店一次性购进排球、足球两种商品共100个,排球每个进价40元,售价50元,足球每个进价90元,售价105元.
(1)设购进排球x个,销售完此两种商品的总利润为y元,求出y与x的函数关系式;
(2)该商家计划最多投入8000元用于购进此两种商品共100件,至少要购进多少个排球?
(3)在(2)的条件下,若售完这些商品,商家可获得最大利润是多少元?
一、单选题
1.函数 自变量 x 的取值范围是( )
A.x≠ 2 B.x> 1
C.x≥ 1 D.x≥ 1 且 x≠2
2.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
A.37.2分钟 B.48分钟 C.30分钟 D.33分钟
3.星期六,小亮从家里骑自行车到同学家去玩,然后返回,图是他离家的路程y(千米)与时间x(分钟)的函数图象,根据图象信息,下列说法不一定正确的是( )
A.小亮到同学家的路程是3千米
B.小亮在同学家逗留的时间是1小时
C.小亮去时走上坡路,回家时走下坡路
D.小亮回家时用的时间比去时用的时间少
4.过点(﹣2,﹣4)的直线是( )
A.y=x﹣2 B.y=x+2 C.y=2x+1 D.y=﹣2x+1
5.若把一次函数y=2x﹣3向上平移5个单位长度,得到图象解析式是( )
A.y=2x B.y=2x+2 C.y=5x﹣3 D.y=﹣x﹣3
6.如图,函数y=2x-4与x轴.y轴交于点(2,0),(0,-4),当-4<y<0时,x的取值范围是( )
A.x<-1 B.-1<x<0 C.0<x<2 D.-1<x<2
7.若直线 沿y轴平移3个单位得到新的直线 ,则b的值为( )
A.-2或4 B.2或-4 C.4或-6 D.-4或6
8.2016年“龙岗年货博览会”在大运中心体育馆展销,小丽从家出发前去购物,途中发现忘了带钱,于是打电话让妈妈马上从家里送来,同时小丽也往回走,遇到妈妈后聊了一会儿,接着继续前往大运中心体育馆.设小丽从家出发后所用时间为t,小丽与体育馆的距离为S,下面能反映S与t的函数关系的大致图象是( )
A. B.
C. D.
9.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
10.在A、B两地之间有汽车站C(C在直线上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶;甲、乙两车离C站的距离,(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇;其中正确的结论有( )
A.1 B.2个 C.3个 D.4个
二、填空题
11.将一次函数y=﹣2x﹣1的图象沿y轴向上平移3个单位后,得到的图象对应的函数关系式为 .
12.如图所示,在三角形 中,已知 ,高 ,动点 由点 沿 向点 移动 不与点 重合 设 的长为 ,三角形 的面积为 ,则 与 之间的关系式为 .
13.如图,直线AB是一次函数y=kx+b的图像,若线段AB的长度为,则此函数的表达式为 .
14.某复印店用电脑编辑并打印一张文稿收费2元,再每复印一张收费0.3元,则总收费y(元)与同样文稿的数量x(张)之间的关系式是 .
15.已知直线y=﹣ 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为 个.
三、解答题
16.已知正比例函数y=(m+2)x中,y的值随x的增大而增大,而正比例函数y=(2m-3)x,y的值随x的增大而减小,且m为整数,你能求出吗?为什么?
17.若直线y=kx+b与直线y=2x+2 关于x轴对称,求y与x的函数关系式.
18.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(3)若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
19.在同一平面直角坐标系中,观察以下直线:y=2x,y=﹣x+6,y=x+2,y=4x﹣4图象的共同特点,若y=kx+5也有该特点,试求满足条件的k值.
20.某企业生产一种收音机,其成本24元.直接由厂家门市部销售,每台售价32元,门市部的销售需消耗费用每月2400元,如果委托商店销售,出厂价每台28元,销售多少台时两种销售方式所获得的利润相等?若销售量达每月2000台,问采用哪种销售方式,取得的利润较多?
21.如图,直线y=-x+6分别与x轴、y轴交于A、B两点;直线y=与AB交于点C,过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
(1)求点C的坐标;
(2)当0<x<5时,求S与t之间的函数关系式;
(3)求(2)中S的最大值.
22.台州市某体育用品商店一次性购进排球、足球两种商品共100个,排球每个进价40元,售价50元,足球每个进价90元,售价105元.
(1)设购进排球x个,销售完此两种商品的总利润为y元,求出y与x的函数关系式;
(2)该商家计划最多投入8000元用于购进此两种商品共100件,至少要购进多少个排球?
(3)在(2)的条件下,若售完这些商品,商家可获得最大利润是多少元?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
