人教版六年级数学下册《圆柱的表面积》课件(共38张PPT)
文档属性
| 名称 | 人教版六年级数学下册《圆柱的表面积》课件(共38张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 15:03:50 | ||
图片预览





文档简介
(共38张PPT)
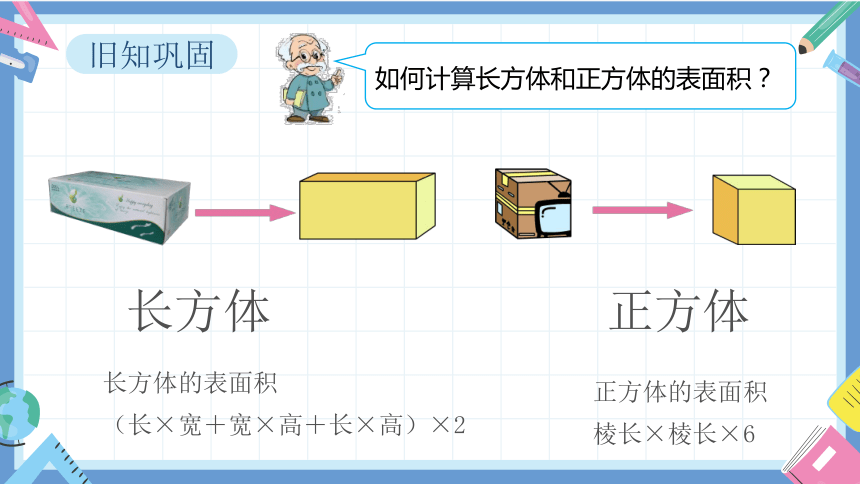
长方体
正方体
旧知巩固
如何计算长方体和正方体的表面积?
长方体的表面积
(长×宽+宽×高+长×高)×2
正方体的表面积
棱长×棱长×6
HAPPY SCHOOL
圆柱的表面积
圆柱的表面积指什么呢?
请摸一摸自己做的圆柱表面,并说一说
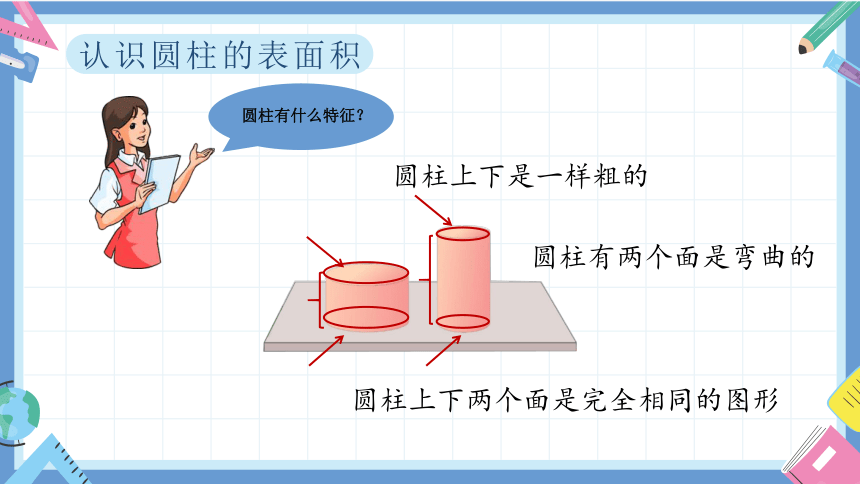
认识圆柱的表面积
圆柱有什么特征?
圆柱上下两个面是完全相同的图形
圆柱有两个面是弯曲的
圆柱上下是一样粗的
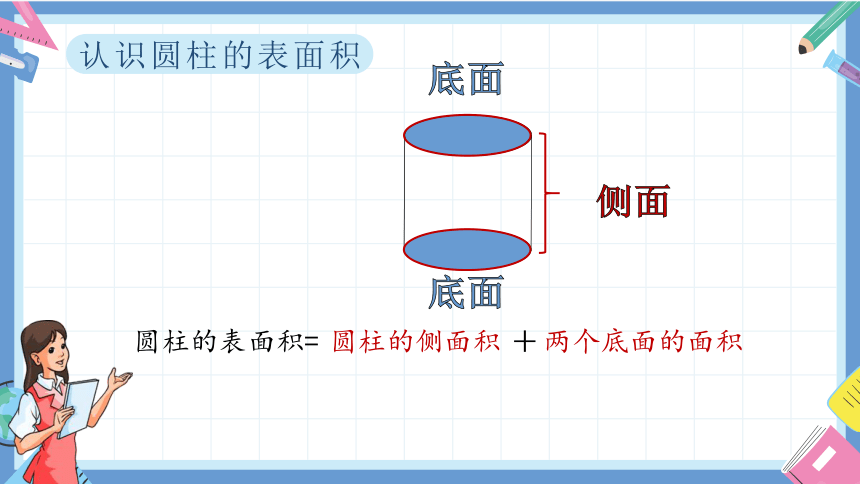
认识圆柱的表面积
圆柱的表面积=
圆柱的侧面积
+
两个底面的面积
侧面
底面
底面
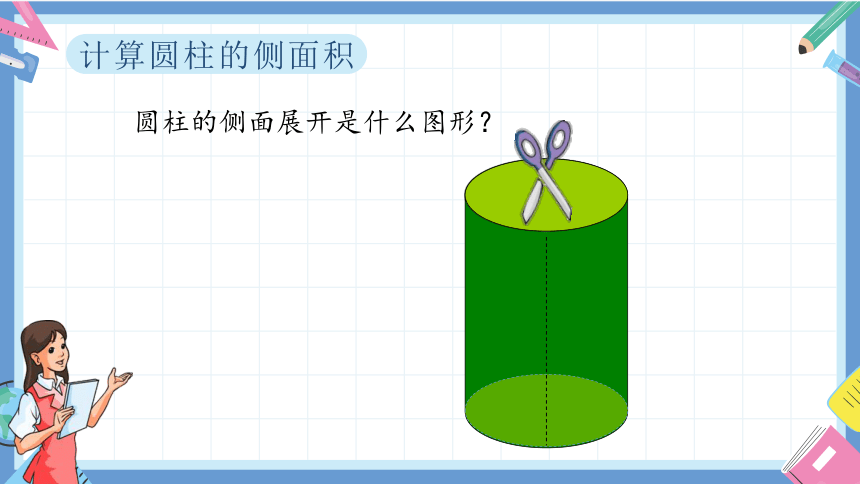
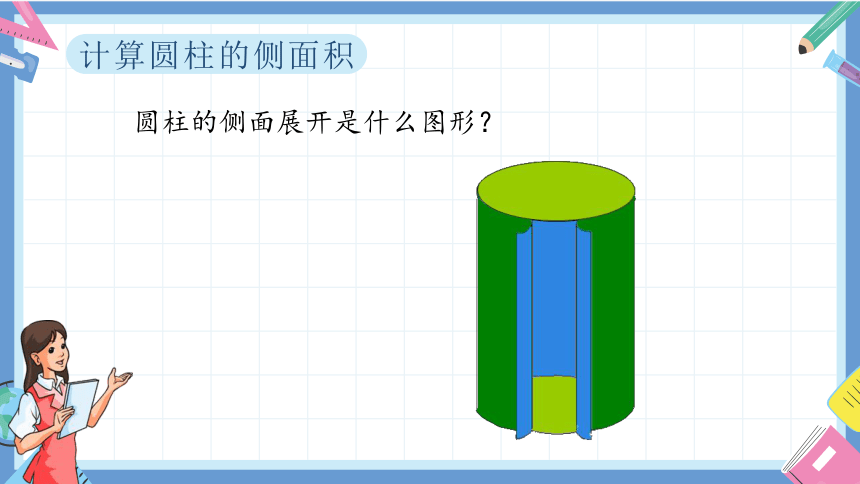
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
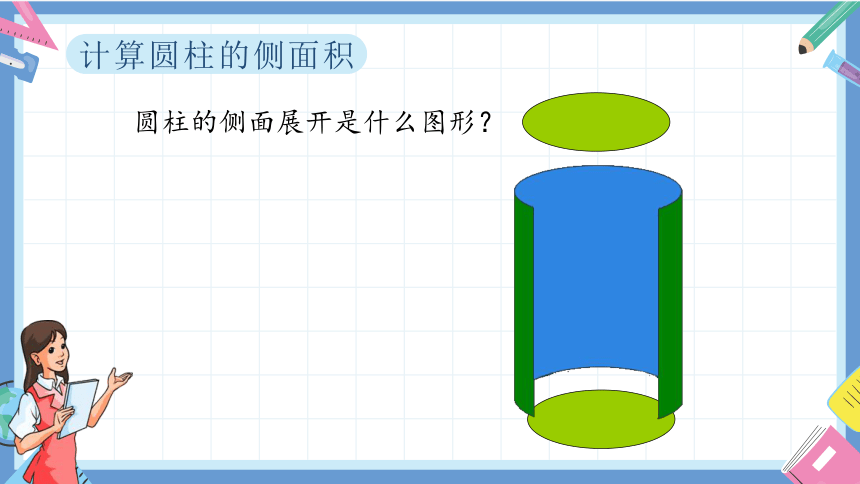
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
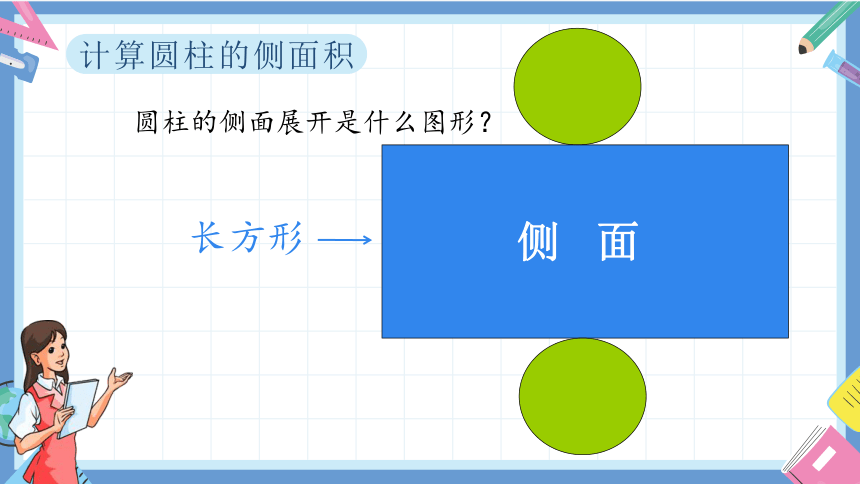
计算圆柱的侧面积
侧 面
圆柱的侧面展开是什么图形?
长方形
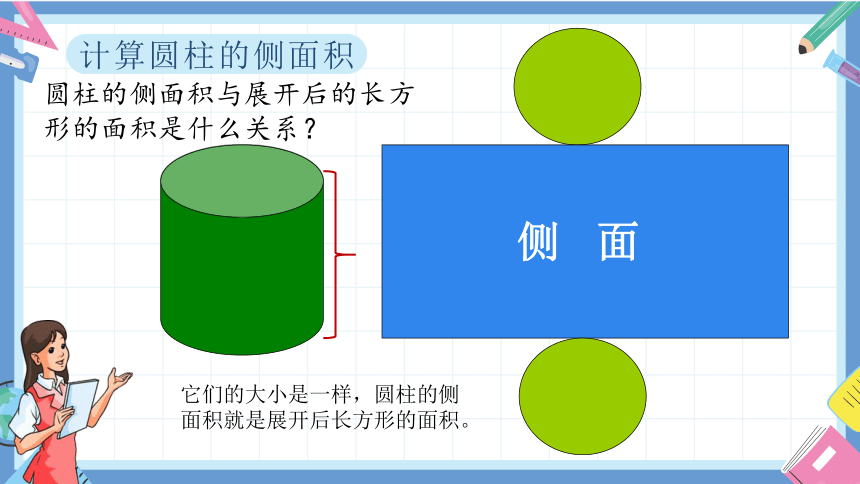
计算圆柱的侧面积
侧 面
圆柱的侧面积与展开后的长方形的面积是什么关系?
它们的大小是一样,圆柱的侧面积就是展开后长方形的面积。
计算圆柱的侧面积
思考如何计算圆柱的侧面积,和同桌讨论你的方法!
只要测量出这个长方形的长和宽,就可以计算圆柱的侧面积了。
展开后的长方形的长就是圆柱底面的周长,长方形的宽就是圆柱的高。
为什么长方形的长就是底面的周长?长方形的宽就是圆柱的高?
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面的周长
高
底面
圆柱侧面积的计算方法是怎样的?
圆柱的侧面积=
圆柱的底面周长
x
高
S侧= Ch
知识点
如果圆柱的底面半径是r,高是h,那么,可以得到下面的公式
圆柱的侧面积=2πrh
其中一个底面的面积=πr
如果圆柱的底面直径是d,高是h,那么,可以得到下面的公式
圆柱的侧面积=πd
其中一个底面的面积=πr
h
运用新知解决问题
一顶圆柱形的厨师帽,高30 cm,帽顶直径20 cm。做这样一顶帽子至少要用多少平方厘米的面料?
(得数保留整十数)
20cm
30cm
这一题要求圆柱的侧面积,请你尝试着自己解决,解决以后请和同桌交流你的想法。
集体交流。
(1)你是怎么想的?
(2)你是怎么列式的?
运用新知解决问题
一顶圆柱形的厨师帽,高30 cm,帽顶直径20 cm。做这样一顶帽子至少要用多少平方厘米的面料?
(得数保留整十数)
20cm
30cm
S侧 =πdh
S底 =πr
S总 =S侧+S底
帽子的侧面积:
帽顶的面积:
需要用的面料:
答:做这样一顶帽子至少要用2200 cm 的面料。
3.14×20×30=1884(cm )
3.14×(20÷2) =314(cm )
1884+314=2198(cm )≈2200(cm )
运用新知解决问题
20cm
30cm
追问1:为什么只计算了一个底面?
因为题目问的是至少要多少平方厘米的布料,如果是2190 cm2的话,那么布料就少了,所以约等于2200 cm2。
追问2:为什么2198 cm 最后约等于2200 cm ,而不是2190 cm 呢?
因为帽子只有一个底是封住的,还有一个底是戴在头上。
通过这一题,我们一定要知道题目所求的问题是什么,并利用数学信息进行分析,最后运用公式进行解答。
巩固新知:一
(1)底面周长是1.6m,高是0.7m。
求下面各圆柱的侧面积
S侧 =Ch
=1.6x0.7
=1.12(m )
答:侧面积是1.12平方米。
巩固新知:一
(2)底面半径是3.2dm,高是5dm。
求下面各圆柱的侧面积
S侧 =2πrh
=2x3.14x3.2x5
答:侧面积是100.48平方分米。
=100.48(dm )
巩固新知:二
5cm
10cm
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是5 cm,高是10 cm。这张商标纸的面积是多少?
小提示
这一题在求什么?
商标纸只在侧面,两个底面没有商标纸。所以这一题要求圆柱的侧面积。请你尝试着自己解决,解决以后请和同桌交流你的想法。
集体交流。
(1)你是怎么想的?
(2)你是怎么列式的?
巩固新知:二
5cm
10cm
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是5 cm,高是10 cm。这张商标纸的面积是多少?
商标纸的面积:2πrh
2×3.14×5×10=314(cm )
答:这张商标纸的面积是314 cm 。
巩固新知:三
小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?(得数保留整十数)
笔筒的侧面积:
答:至少需要用380 cm 彩纸。
3.14×8×13=326.56(cm )
笔筒底面的面积:
3.14×(8÷2) =50.24(cm )
需要用的面料:
326.56+50.24≈380(cm )
S侧 =
S底 =πr
S总 =S侧+S底
13cm
8cm
π
h
d
一
知识点讲解
圆柱的表面积=圆柱侧面积+两个底面的面积
二
知识点讲解
圆柱的侧面积=长方形的面积
=长×宽
=圆柱的底面周长×高
三
总结与归纳
实际用料>计算用料
你有什么收获?
课堂小结
拓展延伸
一个圆柱,高10 cm,底面直径6 cm。将它切成大小相等的2份,表面积最大可增加多少平方厘米?
10cm
6cm
切法一:3.14×(6÷2)2×2=56.52(cm2)。
切法二:10×6×2=120(cm2)
答:表面积最大增加120平方厘米。
56.52<120
课后作业
通过课后作业复习本节课的知识
观察生活中的圆柱体,你能计算它们的表面积吗?
和小伙伴们一起交流一下吧!
THANK VIEWS
好好学习下次再见
长方体
正方体
旧知巩固
如何计算长方体和正方体的表面积?
长方体的表面积
(长×宽+宽×高+长×高)×2
正方体的表面积
棱长×棱长×6
HAPPY SCHOOL
圆柱的表面积
圆柱的表面积指什么呢?
请摸一摸自己做的圆柱表面,并说一说
认识圆柱的表面积
圆柱有什么特征?
圆柱上下两个面是完全相同的图形
圆柱有两个面是弯曲的
圆柱上下是一样粗的
认识圆柱的表面积
圆柱的表面积=
圆柱的侧面积
+
两个底面的面积
侧面
底面
底面
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
计算圆柱的侧面积
圆柱的侧面展开是什么图形?
计算圆柱的侧面积
侧 面
圆柱的侧面展开是什么图形?
长方形
计算圆柱的侧面积
侧 面
圆柱的侧面积与展开后的长方形的面积是什么关系?
它们的大小是一样,圆柱的侧面积就是展开后长方形的面积。
计算圆柱的侧面积
思考如何计算圆柱的侧面积,和同桌讨论你的方法!
只要测量出这个长方形的长和宽,就可以计算圆柱的侧面积了。
展开后的长方形的长就是圆柱底面的周长,长方形的宽就是圆柱的高。
为什么长方形的长就是底面的周长?长方形的宽就是圆柱的高?
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面的周长
高
底面
圆柱侧面积的计算方法是怎样的?
圆柱的侧面积=
圆柱的底面周长
x
高
S侧= Ch
知识点
如果圆柱的底面半径是r,高是h,那么,可以得到下面的公式
圆柱的侧面积=2πrh
其中一个底面的面积=πr
如果圆柱的底面直径是d,高是h,那么,可以得到下面的公式
圆柱的侧面积=πd
其中一个底面的面积=πr
h
运用新知解决问题
一顶圆柱形的厨师帽,高30 cm,帽顶直径20 cm。做这样一顶帽子至少要用多少平方厘米的面料?
(得数保留整十数)
20cm
30cm
这一题要求圆柱的侧面积,请你尝试着自己解决,解决以后请和同桌交流你的想法。
集体交流。
(1)你是怎么想的?
(2)你是怎么列式的?
运用新知解决问题
一顶圆柱形的厨师帽,高30 cm,帽顶直径20 cm。做这样一顶帽子至少要用多少平方厘米的面料?
(得数保留整十数)
20cm
30cm
S侧 =πdh
S底 =πr
S总 =S侧+S底
帽子的侧面积:
帽顶的面积:
需要用的面料:
答:做这样一顶帽子至少要用2200 cm 的面料。
3.14×20×30=1884(cm )
3.14×(20÷2) =314(cm )
1884+314=2198(cm )≈2200(cm )
运用新知解决问题
20cm
30cm
追问1:为什么只计算了一个底面?
因为题目问的是至少要多少平方厘米的布料,如果是2190 cm2的话,那么布料就少了,所以约等于2200 cm2。
追问2:为什么2198 cm 最后约等于2200 cm ,而不是2190 cm 呢?
因为帽子只有一个底是封住的,还有一个底是戴在头上。
通过这一题,我们一定要知道题目所求的问题是什么,并利用数学信息进行分析,最后运用公式进行解答。
巩固新知:一
(1)底面周长是1.6m,高是0.7m。
求下面各圆柱的侧面积
S侧 =Ch
=1.6x0.7
=1.12(m )
答:侧面积是1.12平方米。
巩固新知:一
(2)底面半径是3.2dm,高是5dm。
求下面各圆柱的侧面积
S侧 =2πrh
=2x3.14x3.2x5
答:侧面积是100.48平方分米。
=100.48(dm )
巩固新知:二
5cm
10cm
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是5 cm,高是10 cm。这张商标纸的面积是多少?
小提示
这一题在求什么?
商标纸只在侧面,两个底面没有商标纸。所以这一题要求圆柱的侧面积。请你尝试着自己解决,解决以后请和同桌交流你的想法。
集体交流。
(1)你是怎么想的?
(2)你是怎么列式的?
巩固新知:二
5cm
10cm
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是5 cm,高是10 cm。这张商标纸的面积是多少?
商标纸的面积:2πrh
2×3.14×5×10=314(cm )
答:这张商标纸的面积是314 cm 。
巩固新知:三
小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?(得数保留整十数)
笔筒的侧面积:
答:至少需要用380 cm 彩纸。
3.14×8×13=326.56(cm )
笔筒底面的面积:
3.14×(8÷2) =50.24(cm )
需要用的面料:
326.56+50.24≈380(cm )
S侧 =
S底 =πr
S总 =S侧+S底
13cm
8cm
π
h
d
一
知识点讲解
圆柱的表面积=圆柱侧面积+两个底面的面积
二
知识点讲解
圆柱的侧面积=长方形的面积
=长×宽
=圆柱的底面周长×高
三
总结与归纳
实际用料>计算用料
你有什么收获?
课堂小结
拓展延伸
一个圆柱,高10 cm,底面直径6 cm。将它切成大小相等的2份,表面积最大可增加多少平方厘米?
10cm
6cm
切法一:3.14×(6÷2)2×2=56.52(cm2)。
切法二:10×6×2=120(cm2)
答:表面积最大增加120平方厘米。
56.52<120
课后作业
通过课后作业复习本节课的知识
观察生活中的圆柱体,你能计算它们的表面积吗?
和小伙伴们一起交流一下吧!
THANK VIEWS
好好学习下次再见
