4.2.2等差数列的前n项和公式 课件(共21张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 15:11:46 | ||
图片预览








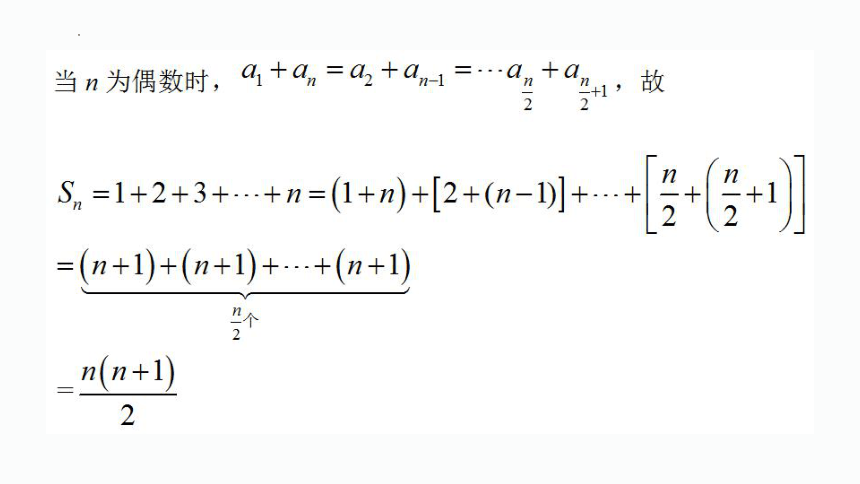
文档简介
(共21张PPT)
4.2.2等差数列的前n项和公式(1)
学习目标:
(1)经历探索等差数列前n项和的过程,类比推理得出等差数列前n项和公式,培养逻辑推理素养;
(2)通过例题的运算,学会运用等差数列的前n项和公式解决一些简单的数学问题,提升数学运算素养;
(3)通过等差数列前n项和公式的推导和公式的简单运用,体会从特殊到一般的思想方法,提高分析问题、解决问题的能力.
【问题1】前面我们学习了等差数列,等差数列的研究路径是什么?
【追问】如何研究等差数列的性质?
背景——定义——表示——性质——应用.
研究数学对象的性质就是研究它的组成要素、相关要素之间的关系,等差数列的定义和性质都是通过“运算”得出的.
本节课继续用运算来研究等差数列的重要性质——等差数列前n项和公式.
问题情境
印度泰姬陵(Taj Mahal)是世界七大建筑奇迹之一,传说当时陵寝中有一个等边三角形图案,以相同大小的圆宝石镶饰而成,共有100层(如下图).你知道这个图案中一共有多少颗宝石吗?
问题2:这其实就是我们所熟悉的高斯算法的故事,高斯是如何快速求出1+2+3+4+…+100的和的?
S100=1+2+3+4+…+100=?
等差数列1,2,···,n,···的前100项和
1+100=101
2+99 =101
3+98 =101
50+51 =101
=50 ×101=5050
计算:S100=1+2+3+4+…+100=?
高斯 Gauss.C.F
(1777~1855)
高斯, 德国数学家. 与阿基米德, 牛顿并称为历史上最伟大的数学家, 有“数学王子”之称.
a1+a100=101
a2+a99 =101
a3+a98 =101
a50+a51=101
=50 ×101=5050
S100=(a1+a100)+ (a2+a99) +…+ (a50+a51)
an=n
首尾配对法
通过配对凑成相同的数,变“多步求和”为“一步相乘”,即将“不同数的求和”转化为“相同数的求和”
【追问1】高斯在求和过程中利用了数列的什么性质?
【追问2】高斯求和法的实质是什么?
将100个不同的数的求和通过配对转化成了50个相同的数的求和,变“多步求和”为“一步相乘”,即化“不同数的求和”为“相同数的求和”.
【追问3】你能用这种方法求数列 的前101项和吗?
【问题3】你能用上述方法求数列 的前n项和吗?
【追问1】在对项数n分奇偶讨论求和的过程中,遇到的难点是什么?
【追问2】如何确定中间的项?
【问题4】在求前n个正整数的和时,对n分奇数、偶数进行讨论得到的结果是一样的,那么怎样避开分类讨论实现“配对”,将“不同数的求和”化归为“相同数的求和”呢?
“奇数加奇数、偶数加偶数”都可以变成偶数,根据这个性质让它自己和自己配对.
倒序相加法
Sn= a1 + a2 + … + an-1 + an
Sn= an + an-1 + … + a2 + a1
【问题5】你能将上述方法推广到求等差数列
的前n项和吗?
【追问1】等差数列前n项和公式有什么特点?
只要知道首项和末项就可以求得前n项和.
用首末两项的平均数代替原来的每一个数,从而将加法简化为乘法.
就是等差数列前n项的平均数的n倍.
这也是等差数列的前n项和公式的另一种形式.
也可以通过
转化为基本量a1和d
利用求和公式和每项具体化
【追问2】只要知道等差数列的首项和公差,数列就完全确定了,那么你能根据等差数列的首项和公差得到它的前n项和公式吗?
【问题6】根据前面的推导过程,你能说出等差数列 的前n项和公式与梯形的面积
公式有什么联系吗?
方程思想
在研究等差数列时,对“知三求二”的问题,一般是转化为基本量(首项、公差)和方程(组)的思想.这种方法是解决数列运算的基本方法,在具体求解过程中应注意已知与未知的联系及方程思想、转化思想的运用.
课堂小结
4.2.2等差数列的前n项和公式(1)
学习目标:
(1)经历探索等差数列前n项和的过程,类比推理得出等差数列前n项和公式,培养逻辑推理素养;
(2)通过例题的运算,学会运用等差数列的前n项和公式解决一些简单的数学问题,提升数学运算素养;
(3)通过等差数列前n项和公式的推导和公式的简单运用,体会从特殊到一般的思想方法,提高分析问题、解决问题的能力.
【问题1】前面我们学习了等差数列,等差数列的研究路径是什么?
【追问】如何研究等差数列的性质?
背景——定义——表示——性质——应用.
研究数学对象的性质就是研究它的组成要素、相关要素之间的关系,等差数列的定义和性质都是通过“运算”得出的.
本节课继续用运算来研究等差数列的重要性质——等差数列前n项和公式.
问题情境
印度泰姬陵(Taj Mahal)是世界七大建筑奇迹之一,传说当时陵寝中有一个等边三角形图案,以相同大小的圆宝石镶饰而成,共有100层(如下图).你知道这个图案中一共有多少颗宝石吗?
问题2:这其实就是我们所熟悉的高斯算法的故事,高斯是如何快速求出1+2+3+4+…+100的和的?
S100=1+2+3+4+…+100=?
等差数列1,2,···,n,···的前100项和
1+100=101
2+99 =101
3+98 =101
50+51 =101
=50 ×101=5050
计算:S100=1+2+3+4+…+100=?
高斯 Gauss.C.F
(1777~1855)
高斯, 德国数学家. 与阿基米德, 牛顿并称为历史上最伟大的数学家, 有“数学王子”之称.
a1+a100=101
a2+a99 =101
a3+a98 =101
a50+a51=101
=50 ×101=5050
S100=(a1+a100)+ (a2+a99) +…+ (a50+a51)
an=n
首尾配对法
通过配对凑成相同的数,变“多步求和”为“一步相乘”,即将“不同数的求和”转化为“相同数的求和”
【追问1】高斯在求和过程中利用了数列的什么性质?
【追问2】高斯求和法的实质是什么?
将100个不同的数的求和通过配对转化成了50个相同的数的求和,变“多步求和”为“一步相乘”,即化“不同数的求和”为“相同数的求和”.
【追问3】你能用这种方法求数列 的前101项和吗?
【问题3】你能用上述方法求数列 的前n项和吗?
【追问1】在对项数n分奇偶讨论求和的过程中,遇到的难点是什么?
【追问2】如何确定中间的项?
【问题4】在求前n个正整数的和时,对n分奇数、偶数进行讨论得到的结果是一样的,那么怎样避开分类讨论实现“配对”,将“不同数的求和”化归为“相同数的求和”呢?
“奇数加奇数、偶数加偶数”都可以变成偶数,根据这个性质让它自己和自己配对.
倒序相加法
Sn= a1 + a2 + … + an-1 + an
Sn= an + an-1 + … + a2 + a1
【问题5】你能将上述方法推广到求等差数列
的前n项和吗?
【追问1】等差数列前n项和公式有什么特点?
只要知道首项和末项就可以求得前n项和.
用首末两项的平均数代替原来的每一个数,从而将加法简化为乘法.
就是等差数列前n项的平均数的n倍.
这也是等差数列的前n项和公式的另一种形式.
也可以通过
转化为基本量a1和d
利用求和公式和每项具体化
【追问2】只要知道等差数列的首项和公差,数列就完全确定了,那么你能根据等差数列的首项和公差得到它的前n项和公式吗?
【问题6】根据前面的推导过程,你能说出等差数列 的前n项和公式与梯形的面积
公式有什么联系吗?
方程思想
在研究等差数列时,对“知三求二”的问题,一般是转化为基本量(首项、公差)和方程(组)的思想.这种方法是解决数列运算的基本方法,在具体求解过程中应注意已知与未知的联系及方程思想、转化思想的运用.
课堂小结
