江苏省常州市部分名校2023-2024学年高二上学期期中质量调研数学试题(PDF版含解析)
文档属性
| 名称 | 江苏省常州市部分名校2023-2024学年高二上学期期中质量调研数学试题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 16:26:00 | ||
图片预览



文档简介
2023-2024学年度第一学期期中质量调研
高二年级
数学试题
2023年11月
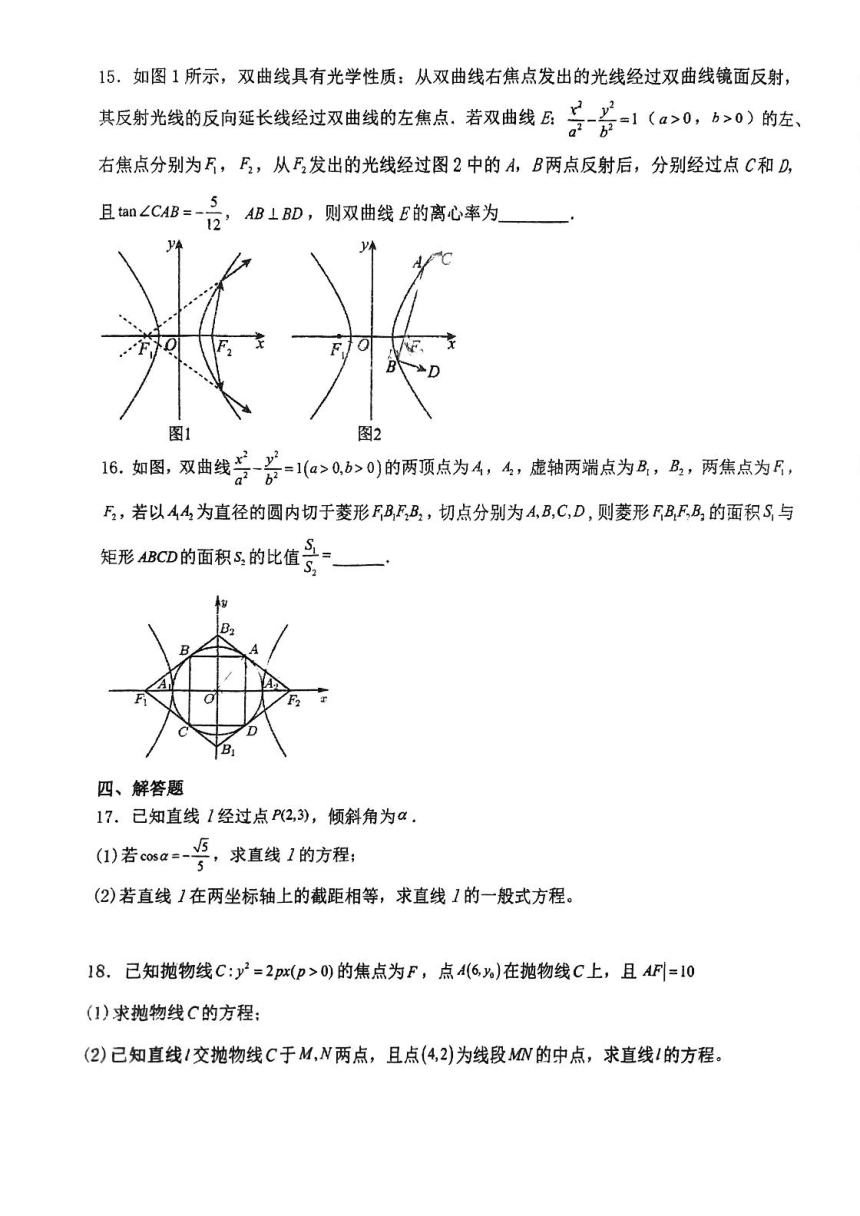
一、单选题
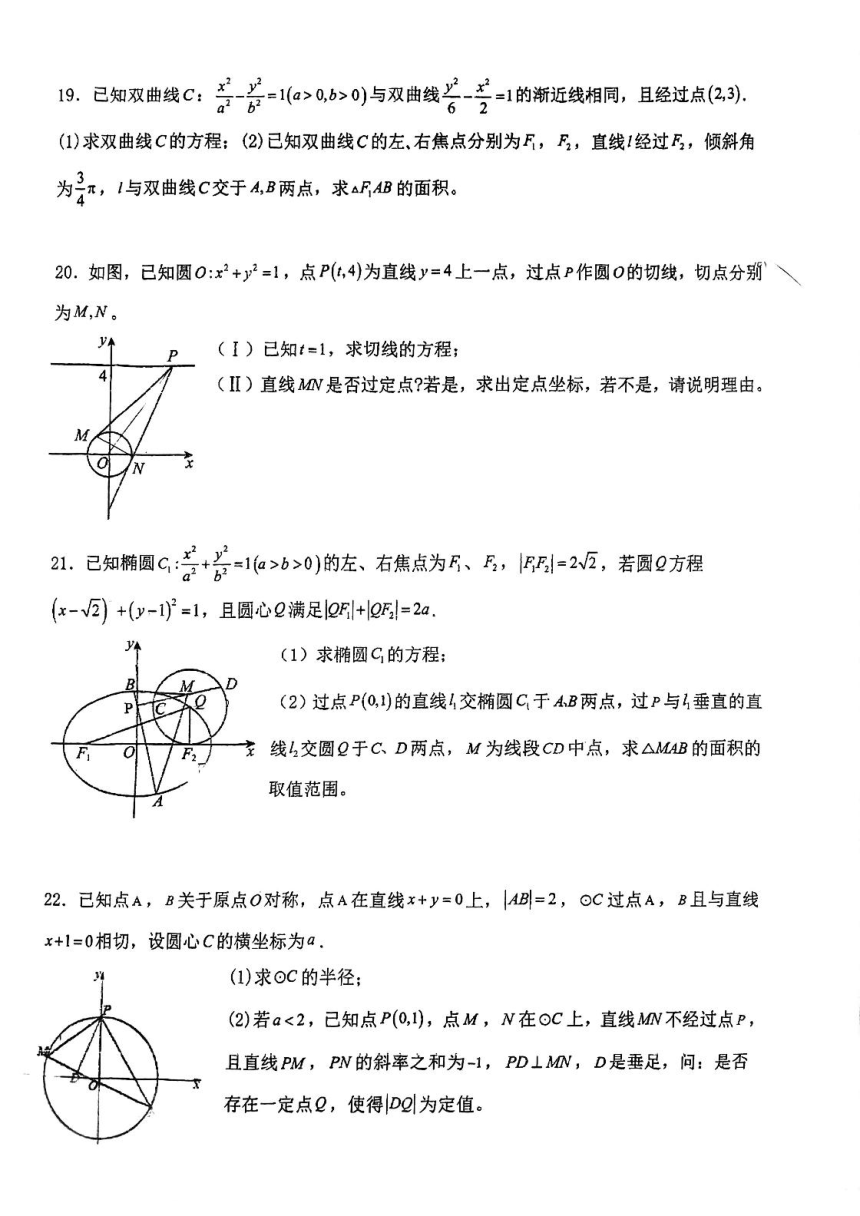
1.抛物线y=的焦点坐标为(
a.(
B.(o
c.
.(
2.已知直线4:3x+y+1=0,12:(a+2)x+y+a=0.当(l2时,a的值为(
)
A.1
B.-3
C.-3或1
D.
3.已知双曲线号若=1>46>0)的右焦点为P,点A在双曲线的渐近线上,△0r是边长
为2的等边三角形.(0为原点),则双曲线的方程为(
A若若1B若-苦1
c音y=1
n皆i
4.直线y=x+b与曲线x=-√2-y2有且仅有一个公共点,则实数b的取值范围是(
A.b=2
B.-√2≤bC.-√2≤b≤V2
D.-√25.已知F是椭圆5x2+9y2=45的左焦点,P是此椭圆上的动点,4(,)是一定点,则P4+P听
的最小值为(
A子
B.
c号
0.号
6.直线(:x-my-2=0(m∈R)与直线:mx+y-2=0交于点A,点B是圆(x+2)+(y+3)=2上的
动点,O为坐标原点,则|AB|的最大值为(
)
A.3W2
B.52
C.5+22
D.3+2N2
7.在平面直角坐标系x0y中,己知圆C:(x-a)2+(y-a-2)2=1,点A(0,3),若圆C上存在点M,
满足MA=2MO,(O为坐标原点),则实数a的取值范围是(
A.【-3,0j
B.(-∞,-3J[0,+∞)℃.[0,3j
D.(-∞0jU[3,+∞)
8已知椭圆G名+发Q>b>0的左,石焦点,乃,过原点的直线1与椭圆C相交于:V
8.
两点.其中N在第一象限。-F5≥9,则椭圆C的离心率的取值范眉为()
A.6-马
B.(0V6-2]
C.(0,5-1]
2
0停-
二、多选题
9.下列结论错误的是(
)
A.过点A(1,3),B(-3,)的直线的倾斜角为30°
B。若直线2x-3y+6=0与直线m+y2=0垂直,则a=号
C、直线x+2y-4=0与直线2x+4y+1=0之间的距离是9
B.已知A(2,3),B(-1,1),点P在x轴上,则PA+PB到的最小值是5
10.设椭圆c:号+=e>6>0的左右焦点为,,P是C上的动点,则下列结论正确的是
(
A.PF+PF =2V2
B.
离心率e=y6
C.△PFF面积的最大值为√互
D.以线段FF为直径的圆与直线x+y-V2=0相切
11.圆O:x2+y-2x=0和圆02:x2+y+4x-6y=0的交点为A,B,则(
)
A,公共弦AB所在直线的方程为x一y=0B.线段AB中垂线的方程为x+y-1=0
C.公共弦B的长为巨
D.A0·A02=-2
12.已知F(-20,R(2,0)是双曲线c导r茶=e>a>0的左,右焦点,且R到C的一条渐近线
的距离为V2,O为坐标原点,点M(,),P为C右支上的一点,则(
)
A.a=b=√2
B.过点M且斜率为1的直线与C有两个不同的交点
C.若PF、PF斜率存在,则kp5ks=1
D.PM+Pl的最小值为2+2√2
三、填空题
13.若直线ar+y-1=0(a>0.b>0)平分圆C:x2y2-2x-4y=0的周长,则ab的最大值为.
14.已知直线1是抛物线C:y2=2x的准线,抛物线的顶点为O,焦点为F,若A为C上一点,
I与C的对称轴交于点B,在△ABF中,sin∠AFB=√2sin∠ABF,则|AB到的值为
高二年级
数学试题
2023年11月
一、单选题
1.抛物线y=的焦点坐标为(
a.(
B.(o
c.
.(
2.已知直线4:3x+y+1=0,12:(a+2)x+y+a=0.当(l2时,a的值为(
)
A.1
B.-3
C.-3或1
D.
3.已知双曲线号若=1>46>0)的右焦点为P,点A在双曲线的渐近线上,△0r是边长
为2的等边三角形.(0为原点),则双曲线的方程为(
A若若1B若-苦1
c音y=1
n皆i
4.直线y=x+b与曲线x=-√2-y2有且仅有一个公共点,则实数b的取值范围是(
A.b=2
B.-√2≤b
D.-√2
的最小值为(
A子
B.
c号
0.号
6.直线(:x-my-2=0(m∈R)与直线:mx+y-2=0交于点A,点B是圆(x+2)+(y+3)=2上的
动点,O为坐标原点,则|AB|的最大值为(
)
A.3W2
B.52
C.5+22
D.3+2N2
7.在平面直角坐标系x0y中,己知圆C:(x-a)2+(y-a-2)2=1,点A(0,3),若圆C上存在点M,
满足MA=2MO,(O为坐标原点),则实数a的取值范围是(
A.【-3,0j
B.(-∞,-3J[0,+∞)℃.[0,3j
D.(-∞0jU[3,+∞)
8已知椭圆G名+发Q>b>0的左,石焦点,乃,过原点的直线1与椭圆C相交于:V
8.
两点.其中N在第一象限。-F5≥9,则椭圆C的离心率的取值范眉为()
A.6-马
B.(0V6-2]
C.(0,5-1]
2
0停-
二、多选题
9.下列结论错误的是(
)
A.过点A(1,3),B(-3,)的直线的倾斜角为30°
B。若直线2x-3y+6=0与直线m+y2=0垂直,则a=号
C、直线x+2y-4=0与直线2x+4y+1=0之间的距离是9
B.已知A(2,3),B(-1,1),点P在x轴上,则PA+PB到的最小值是5
10.设椭圆c:号+=e>6>0的左右焦点为,,P是C上的动点,则下列结论正确的是
(
A.PF+PF =2V2
B.
离心率e=y6
C.△PFF面积的最大值为√互
D.以线段FF为直径的圆与直线x+y-V2=0相切
11.圆O:x2+y-2x=0和圆02:x2+y+4x-6y=0的交点为A,B,则(
)
A,公共弦AB所在直线的方程为x一y=0B.线段AB中垂线的方程为x+y-1=0
C.公共弦B的长为巨
D.A0·A02=-2
12.已知F(-20,R(2,0)是双曲线c导r茶=e>a>0的左,右焦点,且R到C的一条渐近线
的距离为V2,O为坐标原点,点M(,),P为C右支上的一点,则(
)
A.a=b=√2
B.过点M且斜率为1的直线与C有两个不同的交点
C.若PF、PF斜率存在,则kp5ks=1
D.PM+Pl的最小值为2+2√2
三、填空题
13.若直线ar+y-1=0(a>0.b>0)平分圆C:x2y2-2x-4y=0的周长,则ab的最大值为.
14.已知直线1是抛物线C:y2=2x的准线,抛物线的顶点为O,焦点为F,若A为C上一点,
I与C的对称轴交于点B,在△ABF中,sin∠AFB=√2sin∠ABF,则|AB到的值为
同课章节目录
