2.5.1 二次函数与一元二次方程(第1课时) 同步课件(共26张PPT)
文档属性
| 名称 | 2.5.1 二次函数与一元二次方程(第1课时) 同步课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 774.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 09:24:29 | ||
图片预览




文档简介
(共26张PPT)
2.5.1二次函数与一元
二次方程(第1课时)
2、理解二次函数的图像和横轴交点的个数与一元二次方程的根的个数之间的关系。
3、理解二次函数的图像与x轴交点的横坐标是一元二次方程的根,体会数形结合解决问题。
1、经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
学习目标
一元二次方程根的判别式:
式子b -4ac叫做方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母Δ表示.
(1)当Δ>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根.
(2)当Δ=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根.
(3)当Δ<0时,方程ax2+bx+c=0(a≠0)无实数根.
复习回顾
我们学习了一元一次方程kx+b=0(k≠0)和一次函数y=kx+b(k≠0)后,讨论了它们之间的关系.当一次函数中的函数值y=0时,一次函数y=kx+b就转化成了一元一次方程kx+b=0,且一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解.
现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0),它们之间是否也存在一定的关系呢 本节课我们将探索有关问题
创设情境,引入新知
核心知识点一:
二次函数与一元二次方程的关系
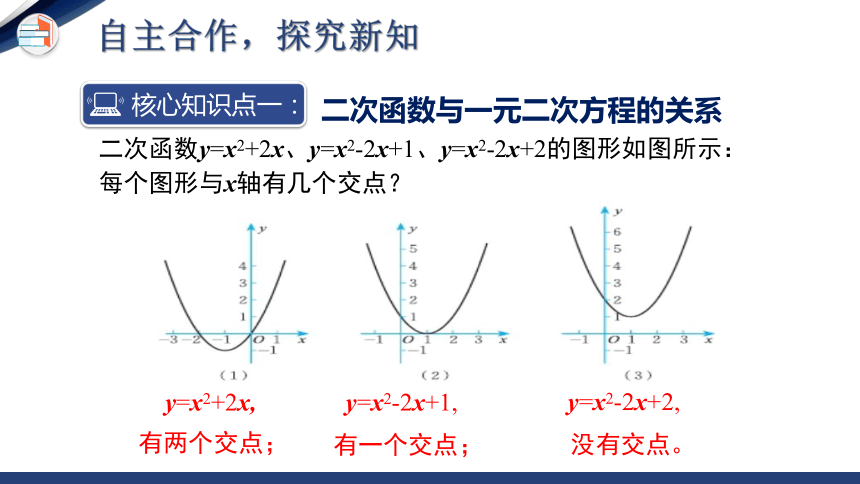
二次函数y=x2+2x、y=x2-2x+1、y=x2-2x+2的图形如图所示:
每个图形与x轴有几个交点?
有两个交点;
有一个交点;
没有交点。
y=x2+2x,
y=x2-2x+1,
y=x2-2x+2,
自主合作,探究新知
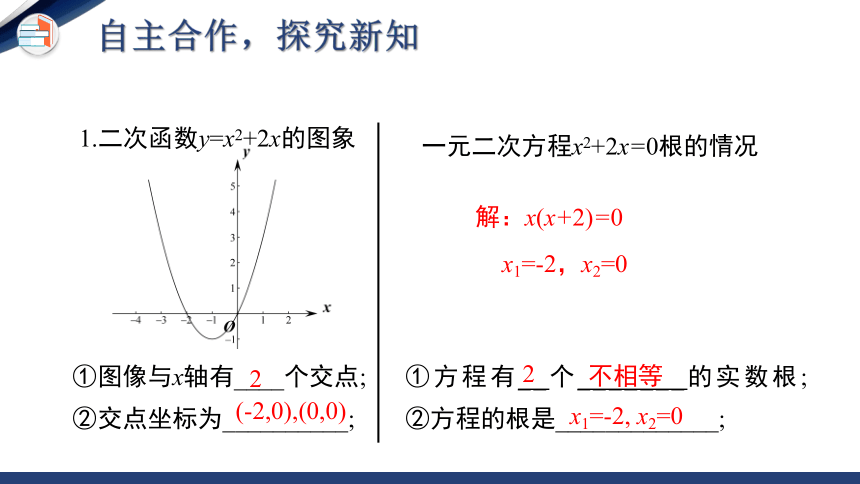
1.二次函数y=x2+2x的图象
①图像与x轴有____个交点;
②交点坐标为__________;
一元二次方程x2+2x=0根的情况
①方程有__个_______的实数根;
②方程的根是_____________;
2
(-2,0),(0,0)
2
不相等
x1=-2, x2=0
解:x(x+2)=0
x1=-2,x2=0
自主合作,探究新知
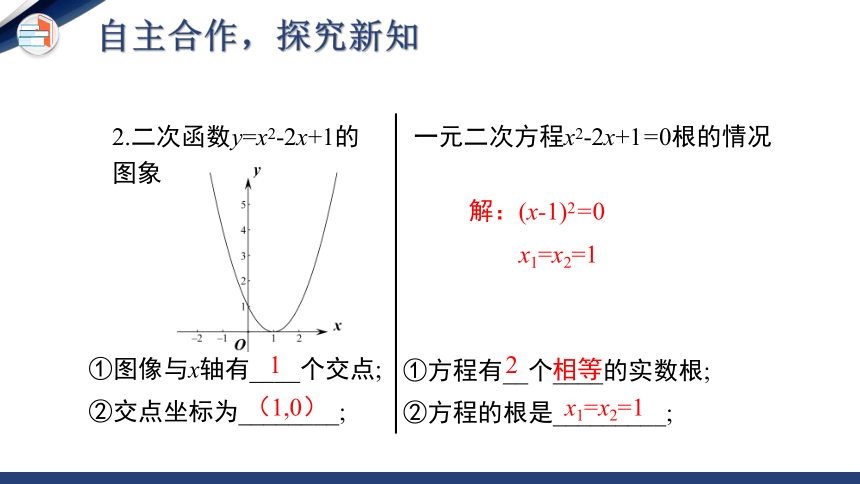
2.二次函数y=x2-2x+1的图象
①图像与x轴有____个交点;
②交点坐标为________;
一元二次方程x2-2x+1=0根的情况
①方程有__个____的实数根;
②方程的根是_________;
1
(1,0)
2
相等
x1=x2=1
解:(x-1)2=0
x1=x2=1
自主合作,探究新知
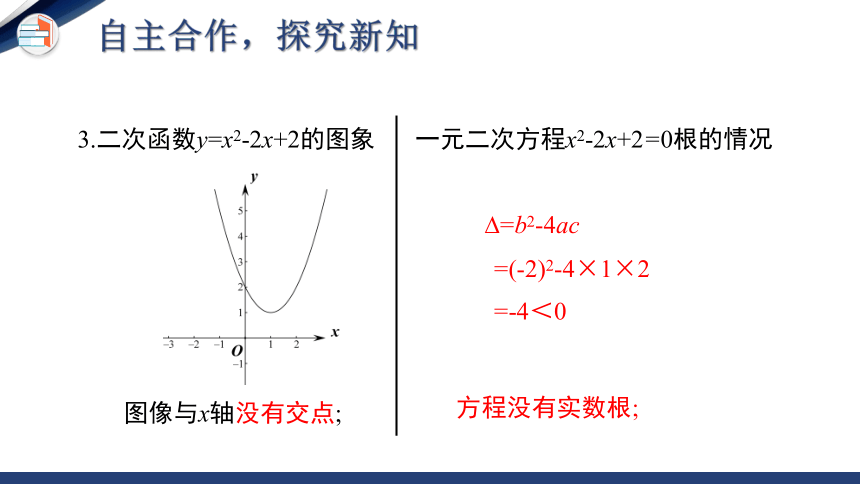
3.二次函数y=x2-2x+2的图象
图像与x轴没有交点;
一元二次方程x2-2x+2=0根的情况
方程没有实数根;
=b2-4ac
=(-2)2-4×1×2
=-4<0
自主合作,探究新知
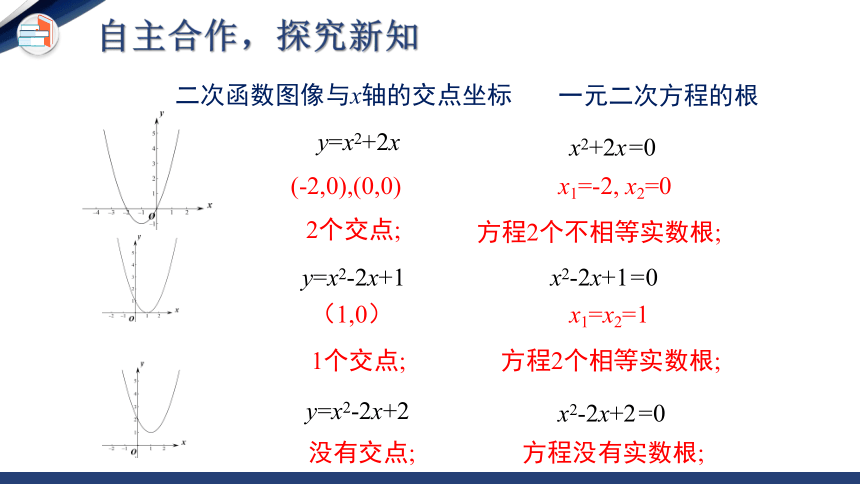
二次函数图像与x轴的交点坐标
y=x2+2x
y=x2-2x+1
y=x2-2x+2
x2+2x=0
x2-2x+1=0
x2-2x+2=0
一元二次方程的根
(-2,0),(0,0)
(1,0)
没有交点;
x1=-2, x2=0
x1=x2=1
方程没有实数根;
2个交点;
1个交点;
方程2个不相等实数根;
方程2个相等实数根;
自主合作,探究新知
归纳总结
有两个不同实根
有两个相同实根
没有根
有两个交点
有一个交点
没有交点
ax2+bx+c = 0 的根
抛物线y=ax2+bx+c与x轴
△= b2 – 4ac
二次函数y=ax2+bx+c的图象与x轴的交点的坐标和一元二次方程ax2+bx+c=0的根的关系:
二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
△ > 0
△ = 0
△ < 0
归纳总结
(-2, 0)
(3, 0)
x1= x2 =5
x1=-3,
x2=4
方程 ax2+bx+c=0
的根
x1=3,
x2=-2
(5, 0)
(4, 0)
(-3, 0)
函数 y=ax2+bx+c与x轴交点坐标
练一练:完成下表:
(5, 0)
(2, 0)
x1=2,
x2=5
牛刀小试
核心知识点二:
运动中的抛物线问题
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
自主合作,探究新知
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
分析:由于小球的飞行高度h与飞行时间t有函数关系h=20t -5t2,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.如果方程有合乎实际的解,则说明小球的飞行高度可以达到问题中h的值;否则,说明小球的飞行高度不能达到问题中h的值.
自主合作,探究新知
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
解:(1)当h=15时,20t-5t2=15,
t2-4t+3=0,
t1=1,t2=3.
当球飞行1s和3s时,它的高度为15m.
自主合作,探究新知
(2)当h=20时,20t-5t2=20,
t2-4t+4=0,
t1=t2=2.
当球飞行2s时,它的高度为20m.
(2)球的飞行高度能否达到 20 m 若能,需要多少时间
自主合作,探究新知
(3)球的飞行高度能否达到 20.5 m 为什么?
(3)当h=20.5时,20t-5t2=20.5,
t2-4t+4.1=0,
因为(-4)2-4×4.1<0,所以方程无实根.
故球的飞行高度达不到20.5m.
自主合作,探究新知
(4)球从飞出到落地要用多少时间
(4)当h=0时,20t-5t2=0,
t2-4t=0,
t1=0,t2=4.
当球飞行0s和4s时,它的高度为0m,
即0s时,球从地面飞出,4s时球落回地面.
自主合作,探究新知
从以上可以看出:
已知二次函数y的值为m,求相应自变量x的值,
就是求相应一元二次方程的解.
例如,已知二次函数y=-x2+4x的值为3,求自变量x
的值.就是求方程3=-x2+4x的解.
例如,解方程x2-4x+3=0,就是已知二次函数y=x2
-4x+3的值为0,求自变量x的值.
自主合作,探究新知
1.已知抛物线y=ax2+bx+c与x轴有两个不同的交点,则关于x的一元二次方程ax2+bx+c=0根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
A
随堂练习
2.小明画了一个函数y=x2+ax+b的图象如图所示,则关于x的方程x2+ax+b=0的解是( ).
A.无解 B.x=1
C.x=-4 D.x=-1或x=4
D
随堂练习
3.二次函数y=ax2+bx+c(a≠0)中,____________决定其图象与x轴交点的个数,当b2-4ac____0时,抛物线与x轴有两个交点;当b2-4ac____0时,抛物线与x轴有一个交点,当b2-4ac____0时,抛物线与x轴没有交点.
4.抛物线y=x2-6x+5,与x轴有____个交点,分别是___________.
5.抛物线y=x2-x+5,与x轴_____交点,且图象都位于x轴的_______.
b2-4ac
=
<
两
(1,0)、(5,0)
没有
上方
>
随堂练习
6.求下列二次函数的图像与x轴的交点.
解:(1)当y=0,
0=x2+4x-5
(1)y=x2+4x-5
解得x1=-5, x2=1
所以二次函数与x轴的交点为 (-5,0), (1,0)
(2)当y=0,
0=-x2+x+2
解得x1=-1, x2=2
所以二次函数与x轴的交点为 (-1,0), (2,0)
(2)y=-x2+x+2
随堂练习
7. 一个足球被从地面向上踢出,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间.
(1)作出函数h=-4.9t2+19.6t的图象;
(2)当t=1,t=2时,足球距地面的高度分别是多少?
(3)方程-4.9t2+19.6t =0, 4.9t2+19.6t =14.7的根的实际意义分别是什么?你能用图象表示出来吗?
解:(1)略
(2)14.7m,19.2m.
(3)足球离开地面及落地的时间,足球高度是14.7m时的时间。
随堂练习
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a ≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a ≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
判别式 的符号
一元二次方程根的情况
Δ
课堂小结
1.布置作业:教材“习题2.10”中第2、3、4题.
2.完成练习册中本课时的练习.
作业布置
2.5.1二次函数与一元
二次方程(第1课时)
2、理解二次函数的图像和横轴交点的个数与一元二次方程的根的个数之间的关系。
3、理解二次函数的图像与x轴交点的横坐标是一元二次方程的根,体会数形结合解决问题。
1、经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
学习目标
一元二次方程根的判别式:
式子b -4ac叫做方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母Δ表示.
(1)当Δ>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根.
(2)当Δ=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根.
(3)当Δ<0时,方程ax2+bx+c=0(a≠0)无实数根.
复习回顾
我们学习了一元一次方程kx+b=0(k≠0)和一次函数y=kx+b(k≠0)后,讨论了它们之间的关系.当一次函数中的函数值y=0时,一次函数y=kx+b就转化成了一元一次方程kx+b=0,且一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解.
现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0),它们之间是否也存在一定的关系呢 本节课我们将探索有关问题
创设情境,引入新知
核心知识点一:
二次函数与一元二次方程的关系
二次函数y=x2+2x、y=x2-2x+1、y=x2-2x+2的图形如图所示:
每个图形与x轴有几个交点?
有两个交点;
有一个交点;
没有交点。
y=x2+2x,
y=x2-2x+1,
y=x2-2x+2,
自主合作,探究新知
1.二次函数y=x2+2x的图象
①图像与x轴有____个交点;
②交点坐标为__________;
一元二次方程x2+2x=0根的情况
①方程有__个_______的实数根;
②方程的根是_____________;
2
(-2,0),(0,0)
2
不相等
x1=-2, x2=0
解:x(x+2)=0
x1=-2,x2=0
自主合作,探究新知
2.二次函数y=x2-2x+1的图象
①图像与x轴有____个交点;
②交点坐标为________;
一元二次方程x2-2x+1=0根的情况
①方程有__个____的实数根;
②方程的根是_________;
1
(1,0)
2
相等
x1=x2=1
解:(x-1)2=0
x1=x2=1
自主合作,探究新知
3.二次函数y=x2-2x+2的图象
图像与x轴没有交点;
一元二次方程x2-2x+2=0根的情况
方程没有实数根;
=b2-4ac
=(-2)2-4×1×2
=-4<0
自主合作,探究新知
二次函数图像与x轴的交点坐标
y=x2+2x
y=x2-2x+1
y=x2-2x+2
x2+2x=0
x2-2x+1=0
x2-2x+2=0
一元二次方程的根
(-2,0),(0,0)
(1,0)
没有交点;
x1=-2, x2=0
x1=x2=1
方程没有实数根;
2个交点;
1个交点;
方程2个不相等实数根;
方程2个相等实数根;
自主合作,探究新知
归纳总结
有两个不同实根
有两个相同实根
没有根
有两个交点
有一个交点
没有交点
ax2+bx+c = 0 的根
抛物线y=ax2+bx+c与x轴
△= b2 – 4ac
二次函数y=ax2+bx+c的图象与x轴的交点的坐标和一元二次方程ax2+bx+c=0的根的关系:
二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
△ > 0
△ = 0
△ < 0
归纳总结
(-2, 0)
(3, 0)
x1= x2 =5
x1=-3,
x2=4
方程 ax2+bx+c=0
的根
x1=3,
x2=-2
(5, 0)
(4, 0)
(-3, 0)
函数 y=ax2+bx+c与x轴交点坐标
练一练:完成下表:
(5, 0)
(2, 0)
x1=2,
x2=5
牛刀小试
核心知识点二:
运动中的抛物线问题
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
自主合作,探究新知
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
分析:由于小球的飞行高度h与飞行时间t有函数关系h=20t -5t2,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.如果方程有合乎实际的解,则说明小球的飞行高度可以达到问题中h的值;否则,说明小球的飞行高度不能达到问题中h的值.
自主合作,探究新知
(1)球的飞行高度能否达到 15 m 若能,需要多少时间
解:(1)当h=15时,20t-5t2=15,
t2-4t+3=0,
t1=1,t2=3.
当球飞行1s和3s时,它的高度为15m.
自主合作,探究新知
(2)当h=20时,20t-5t2=20,
t2-4t+4=0,
t1=t2=2.
当球飞行2s时,它的高度为20m.
(2)球的飞行高度能否达到 20 m 若能,需要多少时间
自主合作,探究新知
(3)球的飞行高度能否达到 20.5 m 为什么?
(3)当h=20.5时,20t-5t2=20.5,
t2-4t+4.1=0,
因为(-4)2-4×4.1<0,所以方程无实根.
故球的飞行高度达不到20.5m.
自主合作,探究新知
(4)球从飞出到落地要用多少时间
(4)当h=0时,20t-5t2=0,
t2-4t=0,
t1=0,t2=4.
当球飞行0s和4s时,它的高度为0m,
即0s时,球从地面飞出,4s时球落回地面.
自主合作,探究新知
从以上可以看出:
已知二次函数y的值为m,求相应自变量x的值,
就是求相应一元二次方程的解.
例如,已知二次函数y=-x2+4x的值为3,求自变量x
的值.就是求方程3=-x2+4x的解.
例如,解方程x2-4x+3=0,就是已知二次函数y=x2
-4x+3的值为0,求自变量x的值.
自主合作,探究新知
1.已知抛物线y=ax2+bx+c与x轴有两个不同的交点,则关于x的一元二次方程ax2+bx+c=0根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
A
随堂练习
2.小明画了一个函数y=x2+ax+b的图象如图所示,则关于x的方程x2+ax+b=0的解是( ).
A.无解 B.x=1
C.x=-4 D.x=-1或x=4
D
随堂练习
3.二次函数y=ax2+bx+c(a≠0)中,____________决定其图象与x轴交点的个数,当b2-4ac____0时,抛物线与x轴有两个交点;当b2-4ac____0时,抛物线与x轴有一个交点,当b2-4ac____0时,抛物线与x轴没有交点.
4.抛物线y=x2-6x+5,与x轴有____个交点,分别是___________.
5.抛物线y=x2-x+5,与x轴_____交点,且图象都位于x轴的_______.
b2-4ac
=
<
两
(1,0)、(5,0)
没有
上方
>
随堂练习
6.求下列二次函数的图像与x轴的交点.
解:(1)当y=0,
0=x2+4x-5
(1)y=x2+4x-5
解得x1=-5, x2=1
所以二次函数与x轴的交点为 (-5,0), (1,0)
(2)当y=0,
0=-x2+x+2
解得x1=-1, x2=2
所以二次函数与x轴的交点为 (-1,0), (2,0)
(2)y=-x2+x+2
随堂练习
7. 一个足球被从地面向上踢出,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间.
(1)作出函数h=-4.9t2+19.6t的图象;
(2)当t=1,t=2时,足球距地面的高度分别是多少?
(3)方程-4.9t2+19.6t =0, 4.9t2+19.6t =14.7的根的实际意义分别是什么?你能用图象表示出来吗?
解:(1)略
(2)14.7m,19.2m.
(3)足球离开地面及落地的时间,足球高度是14.7m时的时间。
随堂练习
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a ≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a ≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
判别式 的符号
一元二次方程根的情况
Δ
课堂小结
1.布置作业:教材“习题2.10”中第2、3、4题.
2.完成练习册中本课时的练习.
作业布置
