3.7 切线长定理 同步课件(共25张PPT)
文档属性
| 名称 | 3.7 切线长定理 同步课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 865.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:49:31 | ||
图片预览






文档简介
(共25张PPT)
3.7 切线长定理
第三章 圆
1.理解切线长的概念,掌握切线长定理.
2.学会运用切线长定理解有关问题.
3.通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,培养数形结合的思想.
学习目标
1、什么叫切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、什么是切线的性质定理?
圆的切线垂直于经过切点的半径.
复习回顾
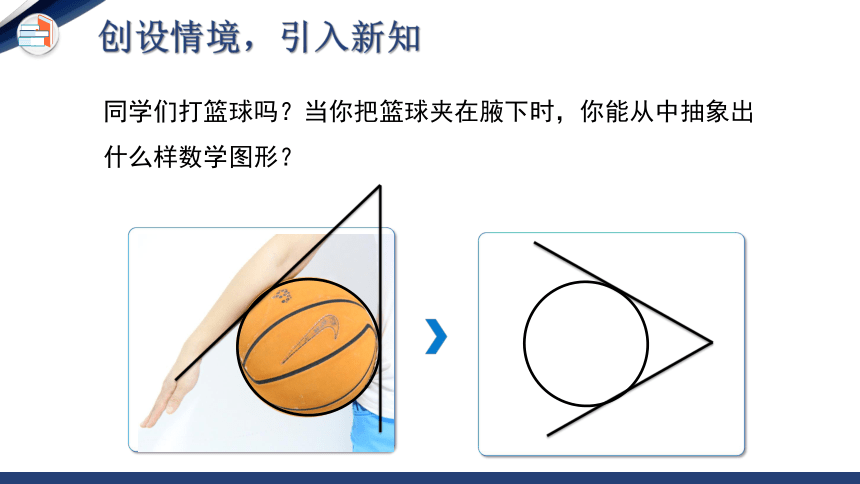
同学们打篮球吗?当你把篮球夹在腋下时,你能从中抽象出什么样数学图形?
创设情境,引入新知
核心知识点一:
切线长定理
B
A
1.如何过⊙O外一点P画出⊙O的切线?
2.这样的切线能画出几条?
O
P
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
自主合作,探究新知
A
B
O
P
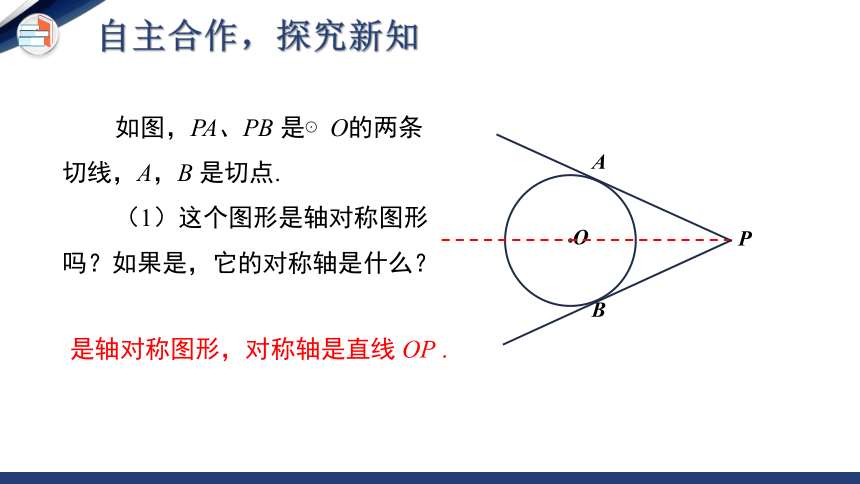
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
自主合作,探究新知
A
B
O
P
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
相等的线段有OA=OB,PA=PB.利用的是对称性
自主合作,探究新知
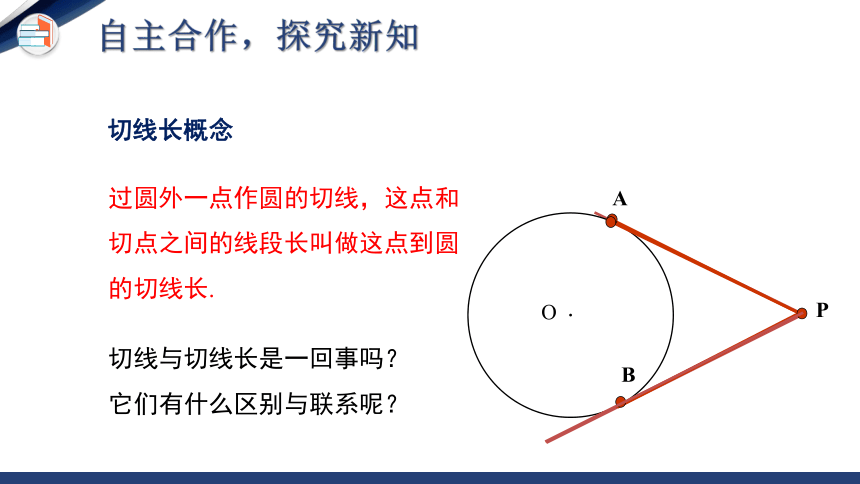
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
自主合作,探究新知
归纳总结
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
切线与切线长
归纳总结
O
P
A
B
证明:连接OA,OB.
∵ PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°.
在Rt△AOP与Rt△BOP中,
∵ OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP.
∴ PA=PB.
已知:如图,PA,PB是⊙O的两条切线,A,B是切点.
求证: PA=PB.
典例解析
归纳总结
切线长定理
∵ PA,PB分别切⊙O于A,B,
∴ PA=PB , OP平分∠APB.
过圆外一点,所画的圆的两条切线的长相等.
几何语言:
O
P
A
B
归纳总结
根据Rt△AOP与Rt△BOP全等,我们还可以得到其他一些什么结论?
O
P
A
B
还可以得到:
∠OPA=∠OPB,
∠POA=∠POB.
从而切线长定理可拓展为:过圆外一点画圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
自主合作,探究新知
拓展:如图是轴对称图形吗?连接图中的两个切点 AB 交 OP 于点 C,又能得出什么结论?请把它们分类.
如图是轴对称图形,连接AB,结论:
①△PAB 是一个等腰三角形, 并且存在等腰三角形的“三线合一”定理.
②AB⊥OP,出现了圆的垂径定理.
自主合作,探究新知
核心知识点二:
外切四边形
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
DN=DP,
AP=AL,
BL=BM,
CN=CM
L
M
N
P
自主合作,探究新知
A
F
O
B
C
E
D
G
H
想一想:将上面四个等式左右两边分别相加,我们能得出什么结论?
圆外切四边形的性质:
圆外切四边形的两组对边和相等.
AE+BE+DG+CG=AH+BF+DH+CF
自主合作,探究新知
1. 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
C
随堂练习
2.如图,PA,PB均为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB平分PD
D
随堂练习
3. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB.
下列结论不一定正确的是( )
A.PA=PB
B.OP垂直平分AB
C.∠OPA=∠OPB
D.PA=AB
D
随堂练习
4. 如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
C
随堂练习
5.如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果AP=4,∠APB=40°,则∠APO= ,PB= .
20°
4
6.△ABC的内切圆⊙O与三边分别切于D,E,F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
A
B
C
F
E
D
O
B
P
O
A
30
随堂练习
7.如图,PA,PB是⊙O的两条切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,求∠P的度数.
解:∵OA=OB,
∴∠BAC=∠OBA=35°,
∴∠AOB=110°.
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
∴∠P=360°-(∠AOB+∠PAO+∠PBO)=360°-(110°+90°+90°)=70°
随堂练习
8.如图,点B在⊙O外,以点B为圆心,OB为半径画⊙B与⊙O相交于两点C,D,与直线OB相交于点A.当AC=5时,求AD的长.
解:连接OC,OD.
∵OA是⊙B的直径,
∴∠OCA=∠ODA=90°,
∴AC,AD都是⊙O的切线,
∴AD=AC=5
随堂练习
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
课堂小结
1. 布置作业:教材“习题3.9”中第1、2、3题.
2.完成练习册中本课时的练习.
作业布置
3.7 切线长定理
第三章 圆
1.理解切线长的概念,掌握切线长定理.
2.学会运用切线长定理解有关问题.
3.通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,培养数形结合的思想.
学习目标
1、什么叫切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、什么是切线的性质定理?
圆的切线垂直于经过切点的半径.
复习回顾
同学们打篮球吗?当你把篮球夹在腋下时,你能从中抽象出什么样数学图形?
创设情境,引入新知
核心知识点一:
切线长定理
B
A
1.如何过⊙O外一点P画出⊙O的切线?
2.这样的切线能画出几条?
O
P
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
自主合作,探究新知
A
B
O
P
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
自主合作,探究新知
A
B
O
P
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
相等的线段有OA=OB,PA=PB.利用的是对称性
自主合作,探究新知
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
自主合作,探究新知
归纳总结
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
切线与切线长
归纳总结
O
P
A
B
证明:连接OA,OB.
∵ PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°.
在Rt△AOP与Rt△BOP中,
∵ OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP.
∴ PA=PB.
已知:如图,PA,PB是⊙O的两条切线,A,B是切点.
求证: PA=PB.
典例解析
归纳总结
切线长定理
∵ PA,PB分别切⊙O于A,B,
∴ PA=PB , OP平分∠APB.
过圆外一点,所画的圆的两条切线的长相等.
几何语言:
O
P
A
B
归纳总结
根据Rt△AOP与Rt△BOP全等,我们还可以得到其他一些什么结论?
O
P
A
B
还可以得到:
∠OPA=∠OPB,
∠POA=∠POB.
从而切线长定理可拓展为:过圆外一点画圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
自主合作,探究新知
拓展:如图是轴对称图形吗?连接图中的两个切点 AB 交 OP 于点 C,又能得出什么结论?请把它们分类.
如图是轴对称图形,连接AB,结论:
①△PAB 是一个等腰三角形, 并且存在等腰三角形的“三线合一”定理.
②AB⊥OP,出现了圆的垂径定理.
自主合作,探究新知
核心知识点二:
外切四边形
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
DN=DP,
AP=AL,
BL=BM,
CN=CM
L
M
N
P
自主合作,探究新知
A
F
O
B
C
E
D
G
H
想一想:将上面四个等式左右两边分别相加,我们能得出什么结论?
圆外切四边形的性质:
圆外切四边形的两组对边和相等.
AE+BE+DG+CG=AH+BF+DH+CF
自主合作,探究新知
1. 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
C
随堂练习
2.如图,PA,PB均为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB平分PD
D
随堂练习
3. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB.
下列结论不一定正确的是( )
A.PA=PB
B.OP垂直平分AB
C.∠OPA=∠OPB
D.PA=AB
D
随堂练习
4. 如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
C
随堂练习
5.如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果AP=4,∠APB=40°,则∠APO= ,PB= .
20°
4
6.△ABC的内切圆⊙O与三边分别切于D,E,F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
A
B
C
F
E
D
O
B
P
O
A
30
随堂练习
7.如图,PA,PB是⊙O的两条切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,求∠P的度数.
解:∵OA=OB,
∴∠BAC=∠OBA=35°,
∴∠AOB=110°.
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
∴∠P=360°-(∠AOB+∠PAO+∠PBO)=360°-(110°+90°+90°)=70°
随堂练习
8.如图,点B在⊙O外,以点B为圆心,OB为半径画⊙B与⊙O相交于两点C,D,与直线OB相交于点A.当AC=5时,求AD的长.
解:连接OC,OD.
∵OA是⊙B的直径,
∴∠OCA=∠ODA=90°,
∴AC,AD都是⊙O的切线,
∴AD=AC=5
随堂练习
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
课堂小结
1. 布置作业:教材“习题3.9”中第1、2、3题.
2.完成练习册中本课时的练习.
作业布置
