第三章 圆 单元小结 课件(共31张PPT)
文档属性
| 名称 | 第三章 圆 单元小结 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 814.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:49:31 | ||
图片预览










文档简介
(共31张PPT)
第三章 圆
单元小结
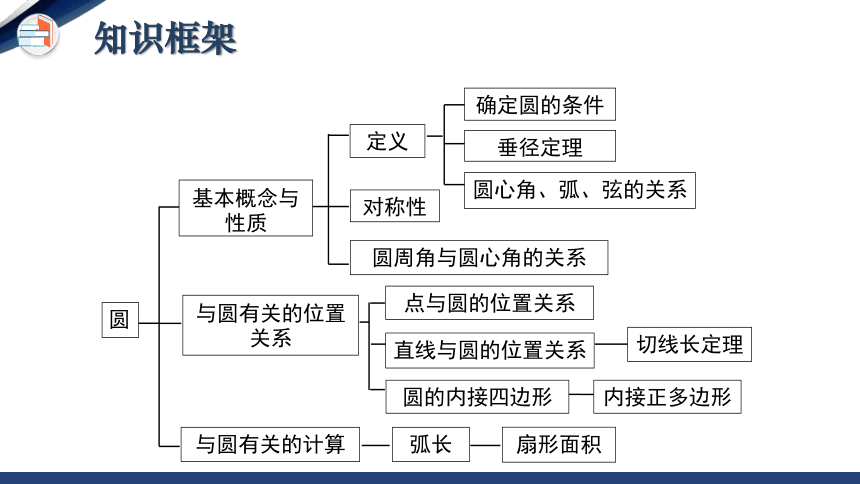
圆
基本概念与性质
与圆有关的位置关系
与圆有关的计算
定义
对称性
点与圆的位置关系
弧长
确定圆的条件
圆周角与圆心角的关系
垂径定理
圆心角、弧、弦的关系
直线与圆的位置关系
圆的内接四边形
扇形面积
切线长定理
内接正多边形
知识框架
一、圆的基本概念及其性质
1. 定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称为______,定长称为半径.如图,以点O为圆心的圆记作⊙O,线段OA叫做半径.
圆心
知识专题
2. 确定圆的条件:
(1)圆心确定圆的位置,________确定圆的大小;
(2)不在同一条直线上的三个点确定一个圆.
半径
知识专题
(1)圆既是轴对称图形又是中心对称图形,对称轴是任意一条____ 所在的直线,对称中心是________。
(2)圆具有旋转不变形,及圆围绕着它的圆心旋转任意角度都能与原来的图形重合。
直径
圆心
3.圆的对称性:
知识专题
4. 与圆有关的概念:
(1)弦:连接圆上任意两点的________叫做弦,如AC、BC;
(2)直径:经过________的弦叫做直径,直径等于半径的2倍;
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧叫做______,如弧ABC,小于半圆的弧叫做______,如AB,BC,AC ;
线段
圆心
优弧
劣弧
⌒
⌒
⌒
⌒
知识专题
(4)半圆:圆上任意一条直径的两个端点分圆成____条弧,每一条弧都叫半圆;
(5)等圆:能够______的两个圆叫做等圆;
(6)等弧:在____________中,能够互相重合的弧叫做等弧;
温馨提示:等弧只存在同圆或等圆中,大小不等的圆中不存在等弧
两
重合
同圆或等圆
知识专题
(7)圆周角:顶点在圆上,并且两边都与圆相交的角叫做圆周角,如∠ACB;
(8)圆心角:顶点在________的角叫做圆心角,如∠AOB;
(9)弦心距:圆心到弦的距离叫做弦心距,如OD.
(10)圆内接四边形:四边形的__________都在圆上,像这样的四边形叫做圆内接四边形。
圆心
四个顶点
知识专题
1. 定理:在同圆或等圆中,相等的圆心角所对的弧____,所对的弦也______;
相等
相等
∴
符号语言:
∵在⊙O中,∠AOB=∠COD
⌒
AB
⌒
CD
=
AB=CD
二、 弦、弧、圆心角的关系
知识专题
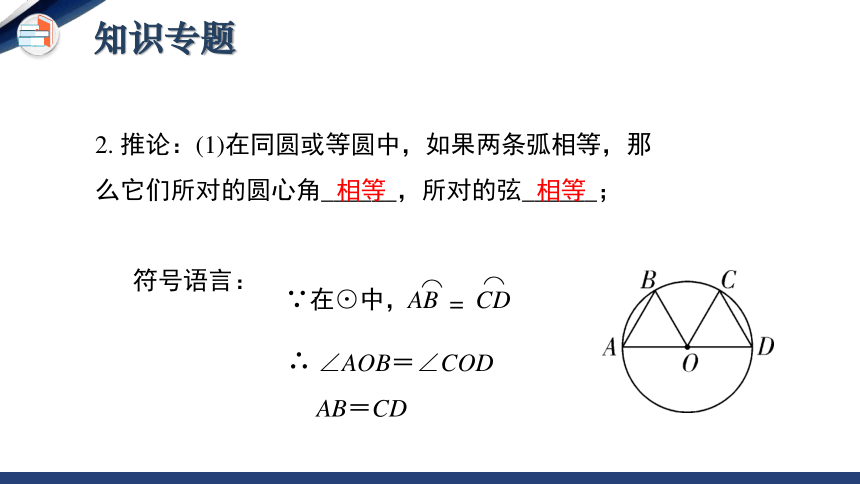
2. 推论:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______,所对的弦______;
符号语言:
相等
相等
∠AOB=∠COD
AB=CD
∵在⊙中,
∴
⌒
AB
⌒
CD
=
知识专题
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧与劣弧分别______;
相等
相等
符号语言:
∵AB=CD
∠AOB=∠COD
∴
⌒
AC
⌒
BD
=
知识专题
注意:(1)理解圆心角、弧、弦三者之间的关系时,必须在同圆或等圆中:
①一条弦对着两条弧,优弧和劣弧;
②等弧和同弧所对应的圆周角有无数个,注意它们之间的相互转化.
(2)在同圆或等圆中,两个圆心角、两条弦、两条弧中如果有一组量相等,则它们所对应的其余各组量也分别相等.
知识专题
2. 推论
(1)同弧或等弧所对的圆周角______;如图,在⊙O中,∠A和____是 所对的圆周角 ∠A=____; ∠A=______;
(2)半圆(或直径)所对的圆周角是___________,90°的圆周角所对的弦是______;如图,在⊙O中,AB是直径 ∠ACB=______.
相等
∠D
∠D
∠BCD
直角(或90°)
直径
90°
⌒
BC
⌒
BD
⌒
BC
=
三、 圆周角定理及其推论
1. 定理:一条弧所对的圆周角等于它所对的圆心角的________.
一半
知识专题
结论:∠AOB=2∠APB. ∠C=∠D,∠A=∠B,△ACE∽△BDE,
此图形称为“蝴蝶模型”
3. 圆周角定理的几种基本图形及结论:
注意:在遇到与直径有关的问题时,一般要构造直径所对的圆周角,由直径转化出直角.
知识专题
1. 定理:垂直于弦的直径______弦,并且______弦所对的两条弧;
符号语言:
∵在⊙O中,CD⊥AB
CD是直径
平分
平分
AM=BM=______AB,
∴
⌒
AC
⌒
BC
=
⌒
AD
⌒
BD
=
四、 垂径定理及其推论
知识专题
2. 推论:平分弦(不是直径)的直径______于弦,并且______弦所对的两条弧;
∵在⊙O中,AM=BM
CD是直径
垂直
平分
符号语言:
CD⊥AB
∴
⌒
AC
⌒
BC
=
⌒
AD
⌒
BD
=
知识专题
注意:垂径定理及其推论的延伸:根据圆的对称性,在以下五个结论中:
① ;② ;③AM=BM;④AB⊥CD;⑤CD是直径,只要满足其中两个结论,另外三个结论一定成立,即“知二推三”.
⌒
AC
⌒
BC
=
⌒
AD
⌒
BD
=
知识专题
五、角形的外接圆及其性质
名称 外接圆
图形
圆心 三角形的外心
圆心位置 三角形三边________________的交点
性质 三角形的外心到三角形三个顶点的距离相等
作图步骤 基本尺规作图
垂直平分线
知识专题
【知识拓展】如图,a、b是Rt△ABC的直角边,c为斜边,则:
①外接圆圆心为AB边的中点;
②外接圆半径R=
知识专题
六、圆内接四边形及其性质
1. 概念:四边形的四个顶点均在同一个圆上的四边形叫做圆的内接四边形.
2. 性质:(1)圆内接四边形的对角________;如图,∠A+∠BCD=180°,∠B+∠D=180°;
(2)圆内接四边形的任意一个角的外角等于它的内对角,如图,∠DCE=______.
互补
∠A
知识专题
考点一 与圆有关的性质
30°
例1:如图所示, 在⊙O中, 直径CD⊥弦AB于点E, 连接OB, CB. 已知⊙O的半径为2, AB= 则∠BCD 的度数为 .
考点专练
【要点指导】垂径定理及其推论是证明两线段相等、两条弧相等及两直 线垂直的重要依据之一. 在有关弦长的计算中常常需要添加辅助线构造直角三 角形, 使问题得以突破与解决. 在解决与圆有关的角度问题时, 应注意圆心角、 圆周角之间的相互转化. 当涉及弦(非直径)所对的弧时应分两种情况:弦(非直 径)所对的弧可能是优弧, 也可能是劣弧.
要点指导
考点二 切线的判定和性质的综合应用
例2.如图所示, △ABC内接于⊙O, CA=CB, CD∥AB且与OA的延长线交于点D.
(1)判断直线CD与⊙O的位置关系,
并说明理由;
(2)若∠ACB=120°, OA=2, 求CD的长.
考点专练
分析: (1)因为CA=CB, 所以考虑连接 OC, 由垂径定理的推论得出OC⊥AB, 进而由CD∥AB证得OC⊥CD.
(2)在 △ODC中, 由边角关系易得CD的长.
考点专练
解 (1)直线CD与⊙O相切.
理由:如图3-Z-5所示, 连接OC.
∵CA=CB, ∴OC⊥AB.
∵CD∥AB, ∴OC⊥CD.
又∵OC是⊙O的半径, ∴直线CD与⊙O相切.
(2)∵CA=CB, ∠ACB=120°,
∴∠ABC=∠BAC=30°, ∴∠DOC=2∠ABC =60°,
∴∠D=90°-∠DOC =30°, ∴OD=2OC=4.
在Rt△ODC中, CD=
考点专练
【要点指导】 (1)证明切线时通常运用下面两种方法: ①若已知直线和圆有公共点, 通常可作出经过该点的半径, 然后证明这条半径和已知直线垂直; ②若未明确说明已知直线和圆是否有公共点, 通常过圆心作这条直线的垂线段, 然后证明这条垂线段的长等于半径.
(2)运用切线的性质时常作过切点的半径解决问题.
要点指导
考点三 与圆有关的计算
例3.如图所示, 在半径为 5, 圆心角等于45°的扇形AOB内部作一个正方形CDEF, 使点C 在OA上, 点D, E在OB上, 点F在 上, 则阴影部分的面积为 . (结果保留π)
考点专练
分析 :如图所示, 连接OF, 由∠COD= 45°, 四边形CDEF是正方形 , 知OD=CD=DE=EF, 于是在Rt△OFE中, OE=2EF.
∵OF= EF 2+OE 2=OF 2,
∴EF 2+(2EF)2=5,
解得EF=1, ∴OD=CD=EF=1,
∴S阴影=S扇形OAB -S△OCD-S正方形CDEF=
考点专练
【要点指导】解决与圆有关的正多边形的计算问题的关键在于适当添加辅助线构造直角三角形,再运用勾股定理来解决问题. 要熟记弧长、扇形 面积的计算公式, 这部分试题常与相关的数学元素、生活情境等结合;求与 圆相关的不规则图形的面积, 一般情况下, 都要借助于圆的有关性质, 并与其他知识相结合, 间接求解.
要点指导
1.布置作业:教材“复习题”中第4、5、7、8、 12 题
2.完成练习册中本课时的练习.
作业布置
第三章 圆
单元小结
圆
基本概念与性质
与圆有关的位置关系
与圆有关的计算
定义
对称性
点与圆的位置关系
弧长
确定圆的条件
圆周角与圆心角的关系
垂径定理
圆心角、弧、弦的关系
直线与圆的位置关系
圆的内接四边形
扇形面积
切线长定理
内接正多边形
知识框架
一、圆的基本概念及其性质
1. 定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称为______,定长称为半径.如图,以点O为圆心的圆记作⊙O,线段OA叫做半径.
圆心
知识专题
2. 确定圆的条件:
(1)圆心确定圆的位置,________确定圆的大小;
(2)不在同一条直线上的三个点确定一个圆.
半径
知识专题
(1)圆既是轴对称图形又是中心对称图形,对称轴是任意一条____ 所在的直线,对称中心是________。
(2)圆具有旋转不变形,及圆围绕着它的圆心旋转任意角度都能与原来的图形重合。
直径
圆心
3.圆的对称性:
知识专题
4. 与圆有关的概念:
(1)弦:连接圆上任意两点的________叫做弦,如AC、BC;
(2)直径:经过________的弦叫做直径,直径等于半径的2倍;
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧叫做______,如弧ABC,小于半圆的弧叫做______,如AB,BC,AC ;
线段
圆心
优弧
劣弧
⌒
⌒
⌒
⌒
知识专题
(4)半圆:圆上任意一条直径的两个端点分圆成____条弧,每一条弧都叫半圆;
(5)等圆:能够______的两个圆叫做等圆;
(6)等弧:在____________中,能够互相重合的弧叫做等弧;
温馨提示:等弧只存在同圆或等圆中,大小不等的圆中不存在等弧
两
重合
同圆或等圆
知识专题
(7)圆周角:顶点在圆上,并且两边都与圆相交的角叫做圆周角,如∠ACB;
(8)圆心角:顶点在________的角叫做圆心角,如∠AOB;
(9)弦心距:圆心到弦的距离叫做弦心距,如OD.
(10)圆内接四边形:四边形的__________都在圆上,像这样的四边形叫做圆内接四边形。
圆心
四个顶点
知识专题
1. 定理:在同圆或等圆中,相等的圆心角所对的弧____,所对的弦也______;
相等
相等
∴
符号语言:
∵在⊙O中,∠AOB=∠COD
⌒
AB
⌒
CD
=
AB=CD
二、 弦、弧、圆心角的关系
知识专题
2. 推论:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______,所对的弦______;
符号语言:
相等
相等
∠AOB=∠COD
AB=CD
∵在⊙中,
∴
⌒
AB
⌒
CD
=
知识专题
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧与劣弧分别______;
相等
相等
符号语言:
∵AB=CD
∠AOB=∠COD
∴
⌒
AC
⌒
BD
=
知识专题
注意:(1)理解圆心角、弧、弦三者之间的关系时,必须在同圆或等圆中:
①一条弦对着两条弧,优弧和劣弧;
②等弧和同弧所对应的圆周角有无数个,注意它们之间的相互转化.
(2)在同圆或等圆中,两个圆心角、两条弦、两条弧中如果有一组量相等,则它们所对应的其余各组量也分别相等.
知识专题
2. 推论
(1)同弧或等弧所对的圆周角______;如图,在⊙O中,∠A和____是 所对的圆周角 ∠A=____; ∠A=______;
(2)半圆(或直径)所对的圆周角是___________,90°的圆周角所对的弦是______;如图,在⊙O中,AB是直径 ∠ACB=______.
相等
∠D
∠D
∠BCD
直角(或90°)
直径
90°
⌒
BC
⌒
BD
⌒
BC
=
三、 圆周角定理及其推论
1. 定理:一条弧所对的圆周角等于它所对的圆心角的________.
一半
知识专题
结论:∠AOB=2∠APB. ∠C=∠D,∠A=∠B,△ACE∽△BDE,
此图形称为“蝴蝶模型”
3. 圆周角定理的几种基本图形及结论:
注意:在遇到与直径有关的问题时,一般要构造直径所对的圆周角,由直径转化出直角.
知识专题
1. 定理:垂直于弦的直径______弦,并且______弦所对的两条弧;
符号语言:
∵在⊙O中,CD⊥AB
CD是直径
平分
平分
AM=BM=______AB,
∴
⌒
AC
⌒
BC
=
⌒
AD
⌒
BD
=
四、 垂径定理及其推论
知识专题
2. 推论:平分弦(不是直径)的直径______于弦,并且______弦所对的两条弧;
∵在⊙O中,AM=BM
CD是直径
垂直
平分
符号语言:
CD⊥AB
∴
⌒
AC
⌒
BC
=
⌒
AD
⌒
BD
=
知识专题
注意:垂径定理及其推论的延伸:根据圆的对称性,在以下五个结论中:
① ;② ;③AM=BM;④AB⊥CD;⑤CD是直径,只要满足其中两个结论,另外三个结论一定成立,即“知二推三”.
⌒
AC
⌒
BC
=
⌒
AD
⌒
BD
=
知识专题
五、角形的外接圆及其性质
名称 外接圆
图形
圆心 三角形的外心
圆心位置 三角形三边________________的交点
性质 三角形的外心到三角形三个顶点的距离相等
作图步骤 基本尺规作图
垂直平分线
知识专题
【知识拓展】如图,a、b是Rt△ABC的直角边,c为斜边,则:
①外接圆圆心为AB边的中点;
②外接圆半径R=
知识专题
六、圆内接四边形及其性质
1. 概念:四边形的四个顶点均在同一个圆上的四边形叫做圆的内接四边形.
2. 性质:(1)圆内接四边形的对角________;如图,∠A+∠BCD=180°,∠B+∠D=180°;
(2)圆内接四边形的任意一个角的外角等于它的内对角,如图,∠DCE=______.
互补
∠A
知识专题
考点一 与圆有关的性质
30°
例1:如图所示, 在⊙O中, 直径CD⊥弦AB于点E, 连接OB, CB. 已知⊙O的半径为2, AB= 则∠BCD 的度数为 .
考点专练
【要点指导】垂径定理及其推论是证明两线段相等、两条弧相等及两直 线垂直的重要依据之一. 在有关弦长的计算中常常需要添加辅助线构造直角三 角形, 使问题得以突破与解决. 在解决与圆有关的角度问题时, 应注意圆心角、 圆周角之间的相互转化. 当涉及弦(非直径)所对的弧时应分两种情况:弦(非直 径)所对的弧可能是优弧, 也可能是劣弧.
要点指导
考点二 切线的判定和性质的综合应用
例2.如图所示, △ABC内接于⊙O, CA=CB, CD∥AB且与OA的延长线交于点D.
(1)判断直线CD与⊙O的位置关系,
并说明理由;
(2)若∠ACB=120°, OA=2, 求CD的长.
考点专练
分析: (1)因为CA=CB, 所以考虑连接 OC, 由垂径定理的推论得出OC⊥AB, 进而由CD∥AB证得OC⊥CD.
(2)在 △ODC中, 由边角关系易得CD的长.
考点专练
解 (1)直线CD与⊙O相切.
理由:如图3-Z-5所示, 连接OC.
∵CA=CB, ∴OC⊥AB.
∵CD∥AB, ∴OC⊥CD.
又∵OC是⊙O的半径, ∴直线CD与⊙O相切.
(2)∵CA=CB, ∠ACB=120°,
∴∠ABC=∠BAC=30°, ∴∠DOC=2∠ABC =60°,
∴∠D=90°-∠DOC =30°, ∴OD=2OC=4.
在Rt△ODC中, CD=
考点专练
【要点指导】 (1)证明切线时通常运用下面两种方法: ①若已知直线和圆有公共点, 通常可作出经过该点的半径, 然后证明这条半径和已知直线垂直; ②若未明确说明已知直线和圆是否有公共点, 通常过圆心作这条直线的垂线段, 然后证明这条垂线段的长等于半径.
(2)运用切线的性质时常作过切点的半径解决问题.
要点指导
考点三 与圆有关的计算
例3.如图所示, 在半径为 5, 圆心角等于45°的扇形AOB内部作一个正方形CDEF, 使点C 在OA上, 点D, E在OB上, 点F在 上, 则阴影部分的面积为 . (结果保留π)
考点专练
分析 :如图所示, 连接OF, 由∠COD= 45°, 四边形CDEF是正方形 , 知OD=CD=DE=EF, 于是在Rt△OFE中, OE=2EF.
∵OF= EF 2+OE 2=OF 2,
∴EF 2+(2EF)2=5,
解得EF=1, ∴OD=CD=EF=1,
∴S阴影=S扇形OAB -S△OCD-S正方形CDEF=
考点专练
【要点指导】解决与圆有关的正多边形的计算问题的关键在于适当添加辅助线构造直角三角形,再运用勾股定理来解决问题. 要熟记弧长、扇形 面积的计算公式, 这部分试题常与相关的数学元素、生活情境等结合;求与 圆相关的不规则图形的面积, 一般情况下, 都要借助于圆的有关性质, 并与其他知识相结合, 间接求解.
要点指导
1.布置作业:教材“复习题”中第4、5、7、8、 12 题
2.完成练习册中本课时的练习.
作业布置
