九年级下册 第一章 直角三角形的边角关系(单元小结) 同步课件(共24张PPT)
文档属性
| 名称 | 九年级下册 第一章 直角三角形的边角关系(单元小结) 同步课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第一章
直角三角形的边角关系
单元小结
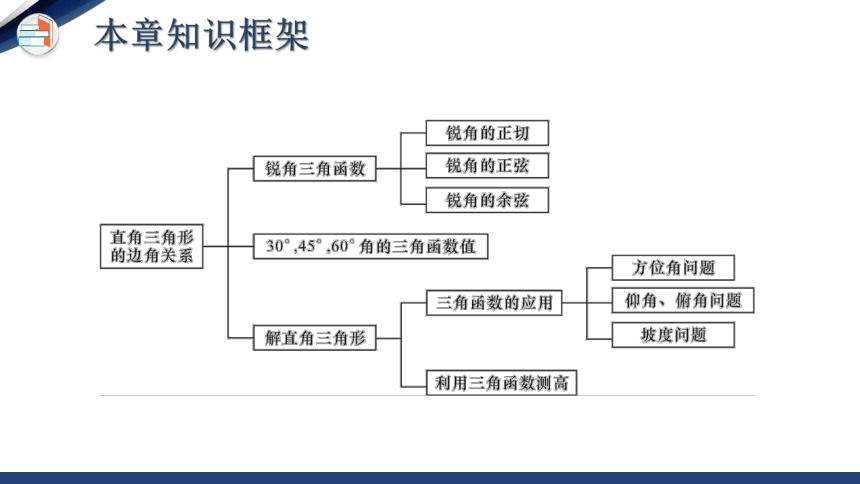
本章知识框架
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90°.
直角三角形三边的关系: 勾股定理 a2+b2=c2.
直角三角形边与角之间的关系:锐角三角函数
知识点一.理解锐角三角函数的概念
知识专题
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:当∠A+∠B=90°.
sinA=cosB
cosA=sinB
tanA·tanB=1
知识专题
b
A
B
C
a
┌
c
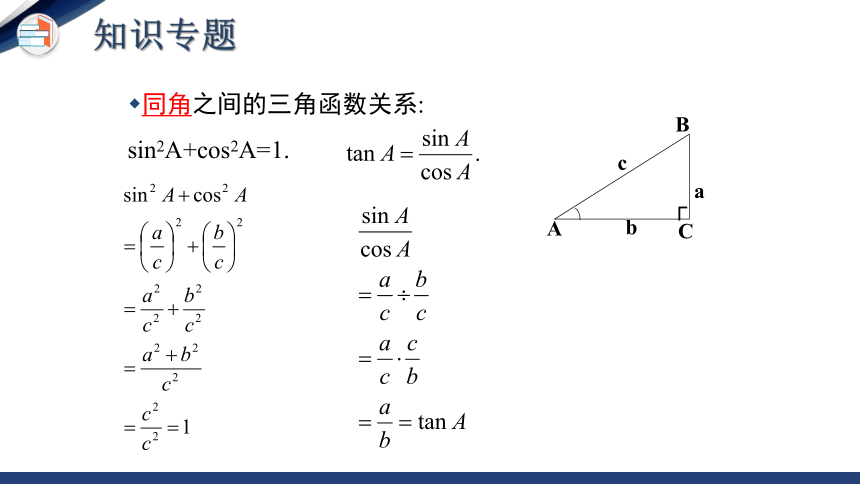
同角之间的三角函数关系:
sin2A+cos2A=1.
知识专题
2
1
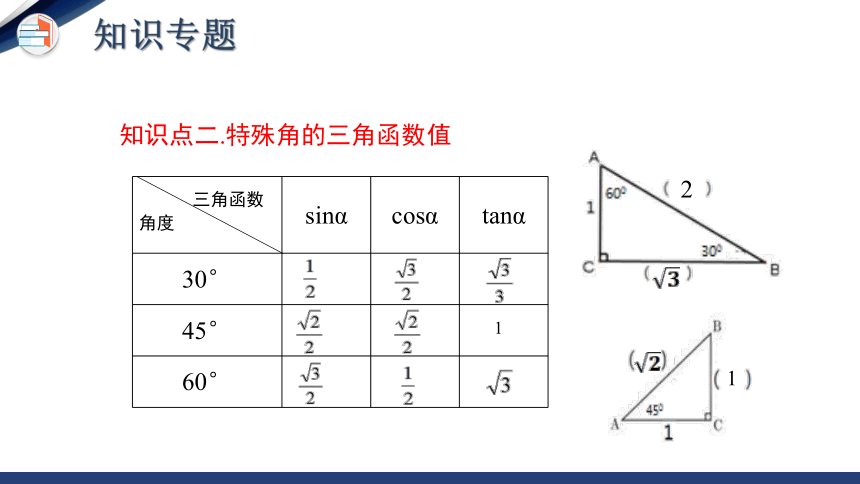
三角函数 角度 sinα cosα tanα
30°
45°
60°
1
知识点二.特殊角的三角函数值
知识专题
当α越大时,sinα越大,tanα越大,cosα反而越小。
若∠A+∠B=90°时,
sinA与cosB的关系是_______________,
tanA与tanB的关系是_______________。
sinA=cosB
tanA·tanB=1
知识专题
由锐角的三角函数值反求锐角
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
知识专题
解直角三角形除了直角外,至少还需要:
1.任意两边的长;
2.任意一边和一个锐角
由直角三角形中已知的元素,求出所有未知元素的过程,
叫做解直角三角形。
知识点三.解直角三角形
直角三角形中有6个元素,分别是三条边和三个角
知识专题
知识点四.三角函数的应用
l
h
α
(1)坡度
i =
h
l
= tanα(α为坡角)
仰角:当从低处观测高处目标时,视线与水平线所成的夹角
俯角:当从高处观测低处目标时,视线与水平线所成的夹角
知识专题
(2)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
方位角:正南(北)或正东(西)方向与目标方向线所成的角
知识专题
图 形
关 系 式 BC=DC-BD =AD·(tan α-tan β) BC=BD+DC
=AD·
【与测量有关的常见图形与关系式】
知识专题
图 形
关 系 式 BD=CE AC=BC·tan α AE=AC+CE AC=
AG=AC+CG
=AC+BE
=
测量底部不可到达的物体的高度
【与测量有关的常见图形与关系式】
测量底部可以到达的物体的高度
a
b
知识专题
专题一 关于锐角三角函数的概念及计算
例1 在△ABC中, ∠A, ∠B, ∠C所对的边分别为a, b, c, 且b2=
(c+a)(c-a), 5b-4c=0, 求sinA+sinB的值.
分析 判断出三角形的形状是关键. 出现比值问题时, 先设出其中的 一份, 再求解;在直角三角形中, 一个锐角的正弦值等于它的对边与斜边之比.
考点专练
解: ∵b2=(c+a)(c-a), ∴b2=c2-a2, 即a2+b2=c2,
∴△ABC是以c为斜边的直角三角形.
∵5b-4c=0,
设b=4k(k>0), 则c=5k, ∴在Rt△ABC中,
考点专练
【要点指导】中考中常借助一定的背景图形(网格、三角形等)通过等量代换及转化, 将某些无法求解的锐角三角函数转移或构建特殊的直角三角形, 借助数形结合求解.
考点专练
专题二 特殊角的三角函数值与实数运算相结合
例2 已知锐角三角形ABC中的∠A与∠B满足(1-tanA)2+
|sinB-
(1)求∠C的度数;
考点专练
考点专练
【要点指导】中考常将特殊角的三角函数值与实数运算相结合来设置运算题, 考查学生对特殊角的三角函数值的掌握情况及实数的运算能力. 熟记特殊角的三角函数值以及实数的运算律、运算法则是解决此类问题的关键.
考点专练
专题三 利用三角函数知识解决实际问题
例3 如图1-Z-2所示(示意图), 小杨在广 场上的A处正面观测一座楼房墙上的广告屏幕, 测得屏幕下端D处的仰角为30° , 然后他正对大楼方向前进5 m到达B处, 又测得该屏幕上端C处的 仰角为45° , 广告屏幕的上端与楼房的顶端平齐. 若该楼高26.65 m, 小杨的眼睛距离
地面1.65 m, 求广告屏幕上端与下端
之间的距离. (结果精确到0.1 m,
考点专练
考点专练
考点专练
【要点指导】 借助图形的性质, 把具体问题中的相关边和角转化到 直角三角形中, 为在直角三角形中运用三角函数的相关知识解决问题创造条件.
考点专练
1、教材“复习题”中第5、6、9、12题.
2、完成练习册中本课时的练习.
作业布置
第一章
直角三角形的边角关系
单元小结
本章知识框架
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90°.
直角三角形三边的关系: 勾股定理 a2+b2=c2.
直角三角形边与角之间的关系:锐角三角函数
知识点一.理解锐角三角函数的概念
知识专题
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:当∠A+∠B=90°.
sinA=cosB
cosA=sinB
tanA·tanB=1
知识专题
b
A
B
C
a
┌
c
同角之间的三角函数关系:
sin2A+cos2A=1.
知识专题
2
1
三角函数 角度 sinα cosα tanα
30°
45°
60°
1
知识点二.特殊角的三角函数值
知识专题
当α越大时,sinα越大,tanα越大,cosα反而越小。
若∠A+∠B=90°时,
sinA与cosB的关系是_______________,
tanA与tanB的关系是_______________。
sinA=cosB
tanA·tanB=1
知识专题
由锐角的三角函数值反求锐角
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
知识专题
解直角三角形除了直角外,至少还需要:
1.任意两边的长;
2.任意一边和一个锐角
由直角三角形中已知的元素,求出所有未知元素的过程,
叫做解直角三角形。
知识点三.解直角三角形
直角三角形中有6个元素,分别是三条边和三个角
知识专题
知识点四.三角函数的应用
l
h
α
(1)坡度
i =
h
l
= tanα(α为坡角)
仰角:当从低处观测高处目标时,视线与水平线所成的夹角
俯角:当从高处观测低处目标时,视线与水平线所成的夹角
知识专题
(2)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
方位角:正南(北)或正东(西)方向与目标方向线所成的角
知识专题
图 形
关 系 式 BC=DC-BD =AD·(tan α-tan β) BC=BD+DC
=AD·
【与测量有关的常见图形与关系式】
知识专题
图 形
关 系 式 BD=CE AC=BC·tan α AE=AC+CE AC=
AG=AC+CG
=AC+BE
=
测量底部不可到达的物体的高度
【与测量有关的常见图形与关系式】
测量底部可以到达的物体的高度
a
b
知识专题
专题一 关于锐角三角函数的概念及计算
例1 在△ABC中, ∠A, ∠B, ∠C所对的边分别为a, b, c, 且b2=
(c+a)(c-a), 5b-4c=0, 求sinA+sinB的值.
分析 判断出三角形的形状是关键. 出现比值问题时, 先设出其中的 一份, 再求解;在直角三角形中, 一个锐角的正弦值等于它的对边与斜边之比.
考点专练
解: ∵b2=(c+a)(c-a), ∴b2=c2-a2, 即a2+b2=c2,
∴△ABC是以c为斜边的直角三角形.
∵5b-4c=0,
设b=4k(k>0), 则c=5k, ∴在Rt△ABC中,
考点专练
【要点指导】中考中常借助一定的背景图形(网格、三角形等)通过等量代换及转化, 将某些无法求解的锐角三角函数转移或构建特殊的直角三角形, 借助数形结合求解.
考点专练
专题二 特殊角的三角函数值与实数运算相结合
例2 已知锐角三角形ABC中的∠A与∠B满足(1-tanA)2+
|sinB-
(1)求∠C的度数;
考点专练
考点专练
【要点指导】中考常将特殊角的三角函数值与实数运算相结合来设置运算题, 考查学生对特殊角的三角函数值的掌握情况及实数的运算能力. 熟记特殊角的三角函数值以及实数的运算律、运算法则是解决此类问题的关键.
考点专练
专题三 利用三角函数知识解决实际问题
例3 如图1-Z-2所示(示意图), 小杨在广 场上的A处正面观测一座楼房墙上的广告屏幕, 测得屏幕下端D处的仰角为30° , 然后他正对大楼方向前进5 m到达B处, 又测得该屏幕上端C处的 仰角为45° , 广告屏幕的上端与楼房的顶端平齐. 若该楼高26.65 m, 小杨的眼睛距离
地面1.65 m, 求广告屏幕上端与下端
之间的距离. (结果精确到0.1 m,
考点专练
考点专练
考点专练
【要点指导】 借助图形的性质, 把具体问题中的相关边和角转化到 直角三角形中, 为在直角三角形中运用三角函数的相关知识解决问题创造条件.
考点专练
1、教材“复习题”中第5、6、9、12题.
2、完成练习册中本课时的练习.
作业布置
