冀教版数学七年级上册单元检测卷 第三章 代数式(测能力)(含解析)
文档属性
| 名称 | 冀教版数学七年级上册单元检测卷 第三章 代数式(测能力)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 405.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 00:00:00 | ||
图片预览



文档简介
代数式
(测能力)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.在,0,,,,,中,是代数式的有( )个.
A.4 B.5 C.6 D.7
2.若,则代数式的值是( )
A.10 B.8 C.6 D.4
3.如图所示,直角三角尺的面积是( )
A. B.
C. D.
4.一块正方形纸片的边长为x,若将一组对边截去2,另一组对边截去3,则剩下的长方形纸片的面积为( )
A. B. C. D.
5.与偶数相邻的两个偶数分别是( ).
A.和 B.和 C.和 D.和
6.据省统计局公布的数据,某市2019年第三季度GDP总值约为a亿元,第四季度GDP总值比第三季度增长了8.5%,受“新型冠状肺炎”疫情的影响,该市2020年第一季度GDP总值比2019年第四季度降低了17.8%,则该市2020年第一季度GDP总值可表示为( )
A.亿元 B.亿元
C.亿元 D.亿元
7.在计数器上,十位上有a个珠子,个位上有4个珠子,则这个计数器表示的数为( )
A.4a B. C. D.
8.下列代数式用自然语言的表示中错误的是( )
A.表示a,b两数的平方和减去它们乘积的2倍
B.表示m与n的2倍的和
C.表示a与b的平方的和
D.表示a,b两数的和与差的乘积
9.用黑白两种颜色的正六边形地板砖按如图所示的规律,拼成如下若干地板图案,为探索出第n个图案中白色地板砖的块数,同学们列出三种不同的算式:
①;
②;
③.
其中正确的算式有( )
A.① B.①② C.②③ D.①②③
10.如图,在第个白球的前面,黑球的个数总共有( )
A.个 B.个 C.个 D.个
二、填空题(每小题4分,共20分)
11.某市出租车收费标准为:起步价4元,2千米后每千米a元,李老师乘车千米,应付款_____元.(只列式不必化简).
12.从甲城到乙城的公路长a千米,一辆汽车从甲城出发,以每小时m千米的速度开往乙城,用含有字母的式子表示:小时后汽车已经行驶了_________千米,此时离乙城还有_________千米.当,时,汽车已经行驶了_________千米,此时离乙城还有_________千米.
13.若一个三位数的个位上的数字是a,十位上的数字比个位上的数字大b,百位上的数字比个位上的数字的平方小2,则这个三位数是__________.(结果要求化简)
14.各位数字不为0的任意三位数,若十位数字等于百位数字与个位数字的和,则我们这个三位数为“平衡数”.
(1)最小的“平衡数”是_________;
(2)若n是一个“平衡数”,且n的各位数字之和为3的倍数,则n最大值为_________.
15.阅读材料:如果欲求的值,可以按照如下步骤进行:
令 ①
等式两边同时乘以2,得
②
由②式减去①式,得
参考以上解答过程可得,_________,其中m为正整数.(结果请用含m的代数式表达)
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)用代数式表示:
(1)a,b两数平方的差;
(2)a,b两数的和与a,b两数的差的积;
(3)x的相反数与y的平方的和;
(4)比x的平方的2倍小a的数;
(5)被5除所得的商为m、余数为2的整数.
17.(8分)某学校艺术社团将举行“庆祝元旦”文艺汇演,需购买m套服装和n个道具.某商店报价为每套服装100元,每个道具15元,并有两种方案供选一种:
方案名称 优惠情况
方案A 总价打8折
方案B 以原价购买,购买一套服装赠送两个道具
(1)若按方案B购买m套服装和n个道具,则需要付费的道具数量是多少?(用含m、n的代数式表示)
(2)当时,试用含n的代数式表示选择方案A与选择方案B所需费用的差额,并直接写出当n满足什么条件时,选择方案A合算?
18.(10分)临近十一,某超市举行“快乐黄金周,优惠你我他”的促销活动,具体方案是“①若一次性消费不超过100元,所购商品按原价支付;②若一次性消费超过100元但不超过300元,按标价给予八折优惠;③若一次性消费超过300元,其中300元以下部分(包括300元)按方案②给予优惠,超过300元的部分给予七折优惠.”若小亮活动期间所购买的商品的原价为元.解答下列问题:
(1)当a大于100元且小于300元时,应付的金额是多少(用含的代数式表示)
(2)当a大于300元时,应付的金额是多少(用含a的代数式表示)
(3)若小亮在活动期间花费220元,请求出其购买商品的原价.
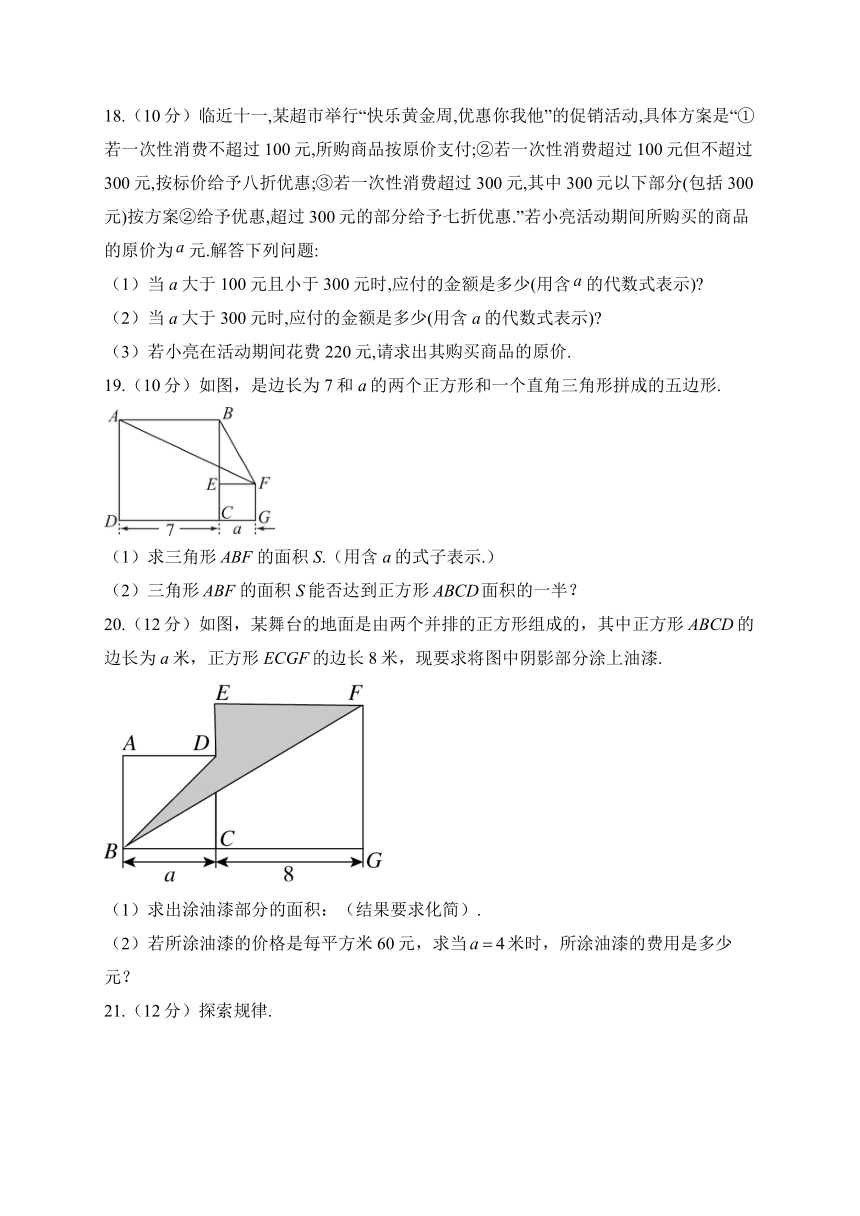
19.(10分)如图,是边长为7和a的两个正方形和一个直角三角形拼成的五边形.
(1)求三角形的面积S.(用含a的式子表示.)
(2)三角形的面积S能否达到正方形面积的一半?
20.(12分)如图,某舞台的地面是由两个并排的正方形组成的,其中正方形ABCD的边长为a米,正方形ECGF的边长8米,现要求将图中阴影部分涂上油漆.
(1)求出涂油漆部分的面积:(结果要求化简).
(2)若所涂油漆的价格是每平方米60元,求当米时,所涂油漆的费用是多少元?
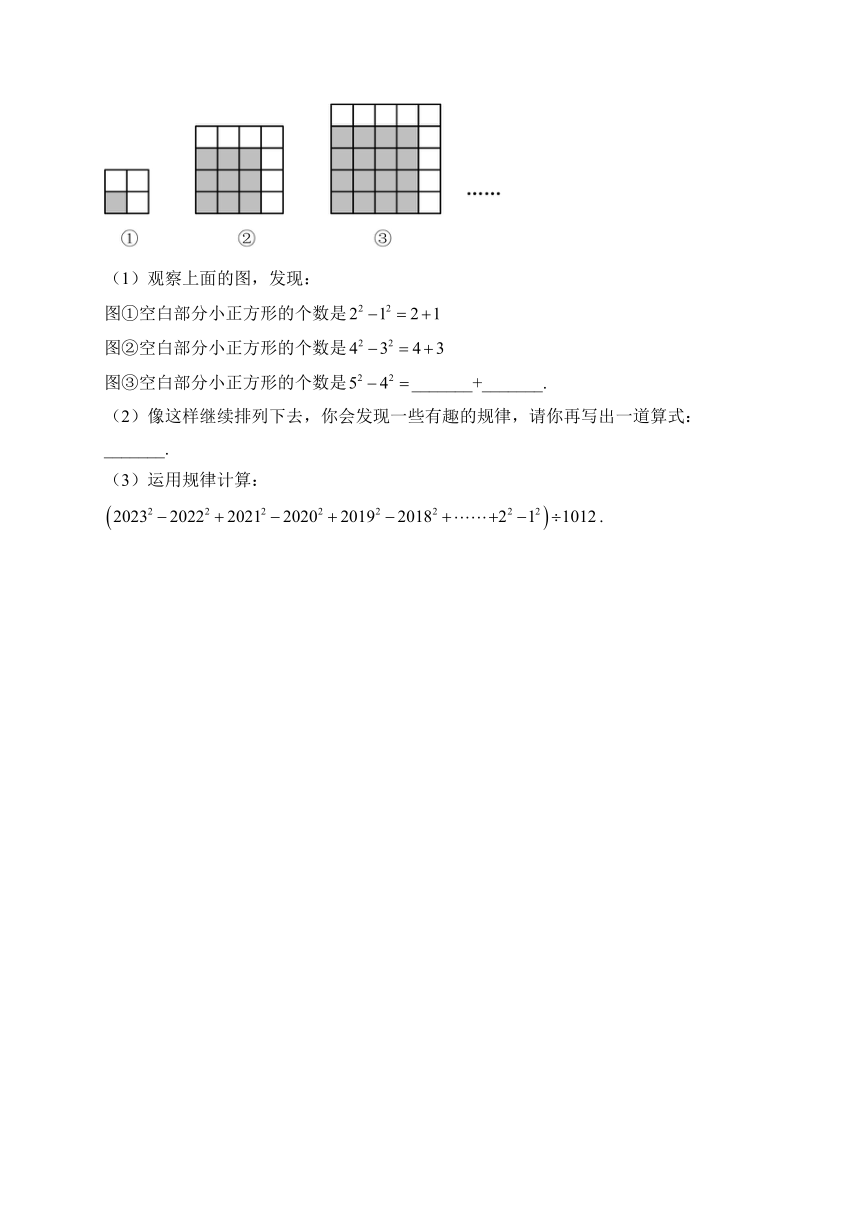
21.(12分)探索规律.
(1)观察上面的图,发现:
图①空白部分小正方形的个数是
图②空白部分小正方形的个数是
图③空白部分小正方形的个数是_______+_______.
(2)像这样继续排列下去,你会发现一些有趣的规律,请你再写出一道算式:_______.
(3)运用规律计算:.
答案以及解析
1.答案:B
解析:,0,,,是代数式;,不是代数式;
代数式有5个;故选B.
2.答案:C
解析:,
,
,故选C.
3.答案:C
解析:由三角形面积公式和圆的面积公式可得,直角三角尺的面积是,
故选C.
4.答案:B
解析:一块正方形纸片的边长为x,若将一组对边截去2,另一组对边截去3,
剩下的长方形纸片的长是,宽是,
面积为.
故答案为B
5.答案:B
解析:由题意得:与偶数相邻的两个偶数分别是和.
故选:B.
6.答案:D
解析:由题意可知,该市2020年第一季度GDP总值可用代数式表示为亿元.故选D.
7.答案:C
解析:在计数器上,十位上有a个珠子,个位上有4个珠子,
这个计数器表示的数为,
故选:C.
8.答案:C
解析:A、表示a,b两数的平方和减去它们乘积的2倍,故正确,符合题意;
B、表示m与n的2倍的和,故正确,符合题意;
C、表示a的平方与b的平方的和,故错误,不符合题意;
D、表示a,b两数的和与差的乘积,故正确,符合题意;
故选:C.
9.答案:D
解析:每个图形都比前一个图形多四个白色的正六边形,所以列式为,或、.
故答案为:D.
10.答案:C
解析:第1个白球与第2个白球之间的黑球的个数为:1,
第2个白球与第3个白球之间的黑球的个数为:2,
第3个白球与第4个白球之间的黑球的个数为:3,
…,
第个白球与第n个白球之间的黑球的个数为:,
在第个白球的前面,黑球的个数总共有:.
故选:C.
11.答案:
解析:由题意可得,李老师乘车千米,应付款为:.
故答案为:.
12.答案:;;54;66
解析:(千米);
(千米),
则0.9小时后汽车已经行驶了千米,此时离乙城还有千米.
把代入得,(千米)
(千米)
故答案为:、;54,66.
13.答案:
解析:该三位数的个位上的数字是a,十位上的数字是,百位上的数字是,故该三位数是.
14.答案:(1)132
(2)891
解析:(1)设十位数字为x,
最小的“平衡数”,
百位数字为1,
个位数字为,且,即,
最小的x的值为3,
最小的“平衡数”是132,
故答案为:132;
(2)设n的百位数字为a,十位数字为b,则个位数字为,
,
n的各位数字之和为3的倍数,则b最大值为9,
a的最大值为8,
n的最大值为891,
故答案为:891.
15.答案:
解析:设①
②,
①-②得到,,
.
故答案为:.
16.答案:(1)
(2)
(3)
(4)
(5)
解析:(1)a,b两数平方的差;;
(2)a,b两数的和与a,b两数的差的积:;
(3)x的相反数与y的平方的和:;
(4)比x的平方的2倍小a的数:;
(5)被5除所得的商为m、余数为2的整数:.
17.答案:(1)
(2)差额:,时,选择方案A合算
解析:(1)方案B:实际费用=元,
(2)当时,方案A的实际费用为元,
方案B的实际费用为元,
选择方案A与选择方案B所需费用的差额:,
当,
解得,
两种方案所花费用相同时.
当时,选择方案A合算;
当时,选择方案B合算;
所以时,选择方案A合算;
答:时,选择方案A合算.
18.答案:(1)0.8a
(2)
(3)275元
解析:(1)当a大于100元且小于300元时,按标价给予八折优惠,所以应付金额是0.8a元.
(2)当a大于300元时,其中有300元是按方案②给予优惠,这部分费用为(元).
超过300元的部分给予七折优惠,这部分费用为元;
应付金额是(元).
(3)(元),
由于220元小于240元,所以小亮参加方案②,按照8折优惠.
所以此商品的原价为(元).
答:小亮购买商品的原价为275元.
19.答案:(1)
(2)不能
解析:(1)由图可知:,
;
(2)当三角形的面积S为正方形面积的一半时,
,
解得:,不符合题意;
三角形的面积S不能达到正方形面积的一半.
20.答案:(1)涂油漆部分的面积是
(2)所涂油漆的费用是1440元
解析:(1)阴影部分的面积为
;
(2)当时,
,
则所涂油漆费用(元).
21.答案:(1)5,4
(2)(答案不唯一)
(3)
解析:(1)图③空白部分小正方形的个数是;
故答案为:5,4;
(2)由:,,,,
可得:,
则:再写出一道算式可以为:;(答案不唯一);
故答案为:(答案不唯一);
(3)
.
(测能力)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.在,0,,,,,中,是代数式的有( )个.
A.4 B.5 C.6 D.7
2.若,则代数式的值是( )
A.10 B.8 C.6 D.4
3.如图所示,直角三角尺的面积是( )
A. B.
C. D.
4.一块正方形纸片的边长为x,若将一组对边截去2,另一组对边截去3,则剩下的长方形纸片的面积为( )
A. B. C. D.
5.与偶数相邻的两个偶数分别是( ).
A.和 B.和 C.和 D.和
6.据省统计局公布的数据,某市2019年第三季度GDP总值约为a亿元,第四季度GDP总值比第三季度增长了8.5%,受“新型冠状肺炎”疫情的影响,该市2020年第一季度GDP总值比2019年第四季度降低了17.8%,则该市2020年第一季度GDP总值可表示为( )
A.亿元 B.亿元
C.亿元 D.亿元
7.在计数器上,十位上有a个珠子,个位上有4个珠子,则这个计数器表示的数为( )
A.4a B. C. D.
8.下列代数式用自然语言的表示中错误的是( )
A.表示a,b两数的平方和减去它们乘积的2倍
B.表示m与n的2倍的和
C.表示a与b的平方的和
D.表示a,b两数的和与差的乘积
9.用黑白两种颜色的正六边形地板砖按如图所示的规律,拼成如下若干地板图案,为探索出第n个图案中白色地板砖的块数,同学们列出三种不同的算式:
①;
②;
③.
其中正确的算式有( )
A.① B.①② C.②③ D.①②③
10.如图,在第个白球的前面,黑球的个数总共有( )
A.个 B.个 C.个 D.个
二、填空题(每小题4分,共20分)
11.某市出租车收费标准为:起步价4元,2千米后每千米a元,李老师乘车千米,应付款_____元.(只列式不必化简).
12.从甲城到乙城的公路长a千米,一辆汽车从甲城出发,以每小时m千米的速度开往乙城,用含有字母的式子表示:小时后汽车已经行驶了_________千米,此时离乙城还有_________千米.当,时,汽车已经行驶了_________千米,此时离乙城还有_________千米.
13.若一个三位数的个位上的数字是a,十位上的数字比个位上的数字大b,百位上的数字比个位上的数字的平方小2,则这个三位数是__________.(结果要求化简)
14.各位数字不为0的任意三位数,若十位数字等于百位数字与个位数字的和,则我们这个三位数为“平衡数”.
(1)最小的“平衡数”是_________;
(2)若n是一个“平衡数”,且n的各位数字之和为3的倍数,则n最大值为_________.
15.阅读材料:如果欲求的值,可以按照如下步骤进行:
令 ①
等式两边同时乘以2,得
②
由②式减去①式,得
参考以上解答过程可得,_________,其中m为正整数.(结果请用含m的代数式表达)
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)用代数式表示:
(1)a,b两数平方的差;
(2)a,b两数的和与a,b两数的差的积;
(3)x的相反数与y的平方的和;
(4)比x的平方的2倍小a的数;
(5)被5除所得的商为m、余数为2的整数.
17.(8分)某学校艺术社团将举行“庆祝元旦”文艺汇演,需购买m套服装和n个道具.某商店报价为每套服装100元,每个道具15元,并有两种方案供选一种:
方案名称 优惠情况
方案A 总价打8折
方案B 以原价购买,购买一套服装赠送两个道具
(1)若按方案B购买m套服装和n个道具,则需要付费的道具数量是多少?(用含m、n的代数式表示)
(2)当时,试用含n的代数式表示选择方案A与选择方案B所需费用的差额,并直接写出当n满足什么条件时,选择方案A合算?
18.(10分)临近十一,某超市举行“快乐黄金周,优惠你我他”的促销活动,具体方案是“①若一次性消费不超过100元,所购商品按原价支付;②若一次性消费超过100元但不超过300元,按标价给予八折优惠;③若一次性消费超过300元,其中300元以下部分(包括300元)按方案②给予优惠,超过300元的部分给予七折优惠.”若小亮活动期间所购买的商品的原价为元.解答下列问题:
(1)当a大于100元且小于300元时,应付的金额是多少(用含的代数式表示)
(2)当a大于300元时,应付的金额是多少(用含a的代数式表示)
(3)若小亮在活动期间花费220元,请求出其购买商品的原价.
19.(10分)如图,是边长为7和a的两个正方形和一个直角三角形拼成的五边形.
(1)求三角形的面积S.(用含a的式子表示.)
(2)三角形的面积S能否达到正方形面积的一半?
20.(12分)如图,某舞台的地面是由两个并排的正方形组成的,其中正方形ABCD的边长为a米,正方形ECGF的边长8米,现要求将图中阴影部分涂上油漆.
(1)求出涂油漆部分的面积:(结果要求化简).
(2)若所涂油漆的价格是每平方米60元,求当米时,所涂油漆的费用是多少元?
21.(12分)探索规律.
(1)观察上面的图,发现:
图①空白部分小正方形的个数是
图②空白部分小正方形的个数是
图③空白部分小正方形的个数是_______+_______.
(2)像这样继续排列下去,你会发现一些有趣的规律,请你再写出一道算式:_______.
(3)运用规律计算:.
答案以及解析
1.答案:B
解析:,0,,,是代数式;,不是代数式;
代数式有5个;故选B.
2.答案:C
解析:,
,
,故选C.
3.答案:C
解析:由三角形面积公式和圆的面积公式可得,直角三角尺的面积是,
故选C.
4.答案:B
解析:一块正方形纸片的边长为x,若将一组对边截去2,另一组对边截去3,
剩下的长方形纸片的长是,宽是,
面积为.
故答案为B
5.答案:B
解析:由题意得:与偶数相邻的两个偶数分别是和.
故选:B.
6.答案:D
解析:由题意可知,该市2020年第一季度GDP总值可用代数式表示为亿元.故选D.
7.答案:C
解析:在计数器上,十位上有a个珠子,个位上有4个珠子,
这个计数器表示的数为,
故选:C.
8.答案:C
解析:A、表示a,b两数的平方和减去它们乘积的2倍,故正确,符合题意;
B、表示m与n的2倍的和,故正确,符合题意;
C、表示a的平方与b的平方的和,故错误,不符合题意;
D、表示a,b两数的和与差的乘积,故正确,符合题意;
故选:C.
9.答案:D
解析:每个图形都比前一个图形多四个白色的正六边形,所以列式为,或、.
故答案为:D.
10.答案:C
解析:第1个白球与第2个白球之间的黑球的个数为:1,
第2个白球与第3个白球之间的黑球的个数为:2,
第3个白球与第4个白球之间的黑球的个数为:3,
…,
第个白球与第n个白球之间的黑球的个数为:,
在第个白球的前面,黑球的个数总共有:.
故选:C.
11.答案:
解析:由题意可得,李老师乘车千米,应付款为:.
故答案为:.
12.答案:;;54;66
解析:(千米);
(千米),
则0.9小时后汽车已经行驶了千米,此时离乙城还有千米.
把代入得,(千米)
(千米)
故答案为:、;54,66.
13.答案:
解析:该三位数的个位上的数字是a,十位上的数字是,百位上的数字是,故该三位数是.
14.答案:(1)132
(2)891
解析:(1)设十位数字为x,
最小的“平衡数”,
百位数字为1,
个位数字为,且,即,
最小的x的值为3,
最小的“平衡数”是132,
故答案为:132;
(2)设n的百位数字为a,十位数字为b,则个位数字为,
,
n的各位数字之和为3的倍数,则b最大值为9,
a的最大值为8,
n的最大值为891,
故答案为:891.
15.答案:
解析:设①
②,
①-②得到,,
.
故答案为:.
16.答案:(1)
(2)
(3)
(4)
(5)
解析:(1)a,b两数平方的差;;
(2)a,b两数的和与a,b两数的差的积:;
(3)x的相反数与y的平方的和:;
(4)比x的平方的2倍小a的数:;
(5)被5除所得的商为m、余数为2的整数:.
17.答案:(1)
(2)差额:,时,选择方案A合算
解析:(1)方案B:实际费用=元,
(2)当时,方案A的实际费用为元,
方案B的实际费用为元,
选择方案A与选择方案B所需费用的差额:,
当,
解得,
两种方案所花费用相同时.
当时,选择方案A合算;
当时,选择方案B合算;
所以时,选择方案A合算;
答:时,选择方案A合算.
18.答案:(1)0.8a
(2)
(3)275元
解析:(1)当a大于100元且小于300元时,按标价给予八折优惠,所以应付金额是0.8a元.
(2)当a大于300元时,其中有300元是按方案②给予优惠,这部分费用为(元).
超过300元的部分给予七折优惠,这部分费用为元;
应付金额是(元).
(3)(元),
由于220元小于240元,所以小亮参加方案②,按照8折优惠.
所以此商品的原价为(元).
答:小亮购买商品的原价为275元.
19.答案:(1)
(2)不能
解析:(1)由图可知:,
;
(2)当三角形的面积S为正方形面积的一半时,
,
解得:,不符合题意;
三角形的面积S不能达到正方形面积的一半.
20.答案:(1)涂油漆部分的面积是
(2)所涂油漆的费用是1440元
解析:(1)阴影部分的面积为
;
(2)当时,
,
则所涂油漆费用(元).
21.答案:(1)5,4
(2)(答案不唯一)
(3)
解析:(1)图③空白部分小正方形的个数是;
故答案为:5,4;
(2)由:,,,,
可得:,
则:再写出一道算式可以为:;(答案不唯一);
故答案为:(答案不唯一);
(3)
.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
