16.2.2 分式的加减法课件(第2课时)
文档属性
| 名称 | 16.2.2 分式的加减法课件(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-07 19:12:32 | ||
图片预览




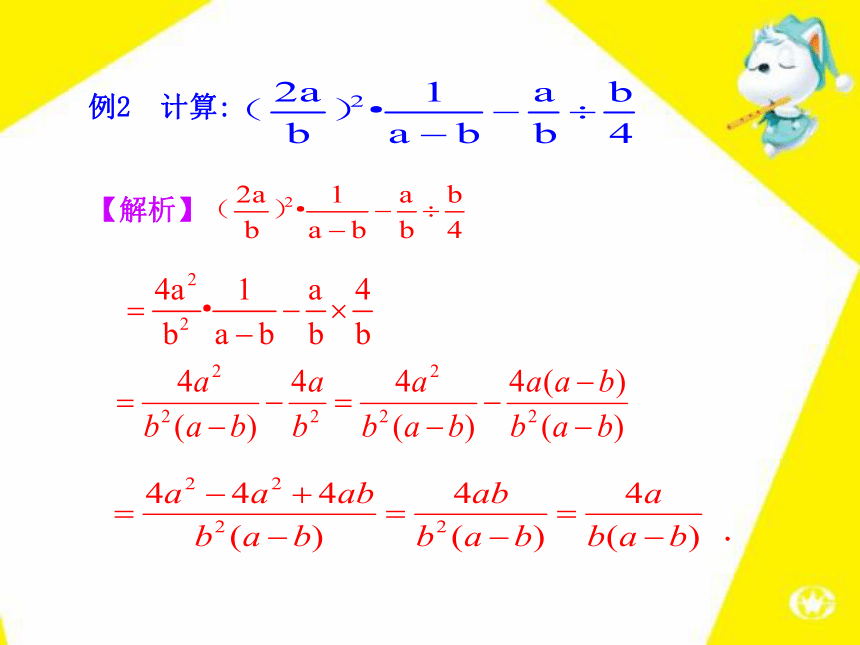



文档简介
课件25张PPT。2 分式的加减法
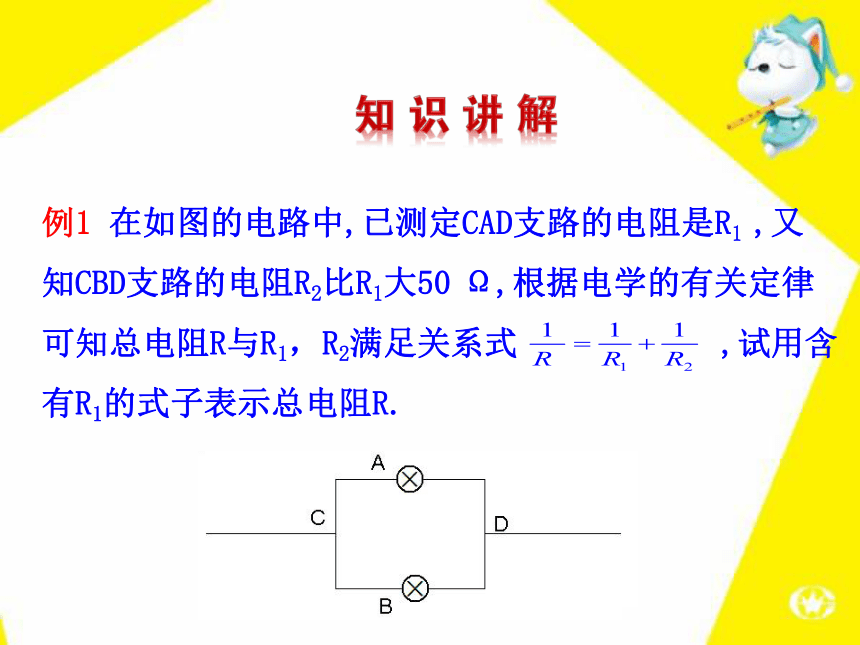
(第2课时)2.能运用分式的混合运算解决实际问题.1.掌握分式混合运算的顺序,能熟练进行分式的混合运算.1.分式的加减法则:2.分式的乘除法则:例1 在如图的电路中,已测定CAD支路的电阻是R1 ,又
知CBD支路的电阻R2比R1大50 Ω,根据电学的有关定律
可知总电阻R与R1,R2满足关系式 ,试用含
有R1的式子表示总电阻R.例2 计算:【解析】.1.化简 的结果是( )
A.a-b B.a+b C. D.【解析】选B.【跟踪训练】2.计算: =( )
A. B. C. D.
【解析】选A.原式=3.用两种方法计算: =解:(按运算顺序)
原式=(利用乘法分配律)
原式例3 根据规划设计,某市工程队准备在开发区修建一条长1120m的盲道,由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10m,从而缩短了工期,假设原计划每天修建盲道x m,那么(2)实际修建这条盲道的工期比原计划缩短了几天?(1)原计划修建这条盲道需多少天?实际修建这条盲道用了多少天?【解析】(1)原计划修建需 天,实际修建需 天.(2)实际修建比原计划缩短了 (天).在一段坡路,小明骑自行车上坡时的速度为每小时v1 km,
下坡时的速度为每小时v2 km,则他在这段路上、下坡的平
均速度是每小时( )
A. km B. km
C. km D.无法确定
【解析】选C.设这段路长为s km,小明上坡用 h,下
坡用 h,上、下坡的平均速度为【跟踪训练】2.化简 其结果是( )
A. B. C. D.
【解析】
4.(凉山·中考)已知:x2-4x+4与|y-1|互为相反数,
则式子( )÷(x+y)的值等于_______.
【解析】由题意知(x2-4x+4)+|y-1|=0,
即(x-2)2+|y-1|=0,∴x=2,y=1.5.对于公式 (f2≠f),若已知f,f2,则f1=______.
【解析】∵答案:7.(河南·中考)已知
将它们组合成(A-B)÷C或A-B÷C的形式,请你从中任
选一种进行计算,先化简,再求值,其中x=3.【解析】选一:(A-B)÷C=
当x=3时,原式=8.(株洲·中考)当x=-2时,求 的值.【解析】原式= 当 时,
原式 9.(贵阳·中考)先化简: 当b=-1时,再
从-2在-2①若a=-1,分式 无意义;
②若a=0,分式 无意义;
③若a=1,分式 无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在).本课时我们学习了
1.分式的混合运算
运算顺序:(1)先乘方,再乘除,然后加减.如果有括号,先算括号里面的.
(2)分式的加减、乘除都是分式的同级运算,同级运算是按从左往右的顺序运算.进行分式混合运算时注意:
(1)正确运用运算法则;(2)灵活运用运算律;
(3)运算结果要化简,使结果为最简分式或整式.
2.分式加减在实际问题中的应用. 顽强的毅力可以征服世界上任何一座高峰!
—— 狄更斯
(第2课时)2.能运用分式的混合运算解决实际问题.1.掌握分式混合运算的顺序,能熟练进行分式的混合运算.1.分式的加减法则:2.分式的乘除法则:例1 在如图的电路中,已测定CAD支路的电阻是R1 ,又
知CBD支路的电阻R2比R1大50 Ω,根据电学的有关定律
可知总电阻R与R1,R2满足关系式 ,试用含
有R1的式子表示总电阻R.例2 计算:【解析】.1.化简 的结果是( )
A.a-b B.a+b C. D.【解析】选B.【跟踪训练】2.计算: =( )
A. B. C. D.
【解析】选A.原式=3.用两种方法计算: =解:(按运算顺序)
原式=(利用乘法分配律)
原式例3 根据规划设计,某市工程队准备在开发区修建一条长1120m的盲道,由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10m,从而缩短了工期,假设原计划每天修建盲道x m,那么(2)实际修建这条盲道的工期比原计划缩短了几天?(1)原计划修建这条盲道需多少天?实际修建这条盲道用了多少天?【解析】(1)原计划修建需 天,实际修建需 天.(2)实际修建比原计划缩短了 (天).在一段坡路,小明骑自行车上坡时的速度为每小时v1 km,
下坡时的速度为每小时v2 km,则他在这段路上、下坡的平
均速度是每小时( )
A. km B. km
C. km D.无法确定
【解析】选C.设这段路长为s km,小明上坡用 h,下
坡用 h,上、下坡的平均速度为【跟踪训练】2.化简 其结果是( )
A. B. C. D.
【解析】
4.(凉山·中考)已知:x2-4x+4与|y-1|互为相反数,
则式子( )÷(x+y)的值等于_______.
【解析】由题意知(x2-4x+4)+|y-1|=0,
即(x-2)2+|y-1|=0,∴x=2,y=1.5.对于公式 (f2≠f),若已知f,f2,则f1=______.
【解析】∵答案:7.(河南·中考)已知
将它们组合成(A-B)÷C或A-B÷C的形式,请你从中任
选一种进行计算,先化简,再求值,其中x=3.【解析】选一:(A-B)÷C=
当x=3时,原式=8.(株洲·中考)当x=-2时,求 的值.【解析】原式= 当 时,
原式 9.(贵阳·中考)先化简: 当b=-1时,再
从-2
②若a=0,分式 无意义;
③若a=1,分式 无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在).本课时我们学习了
1.分式的混合运算
运算顺序:(1)先乘方,再乘除,然后加减.如果有括号,先算括号里面的.
(2)分式的加减、乘除都是分式的同级运算,同级运算是按从左往右的顺序运算.进行分式混合运算时注意:
(1)正确运用运算法则;(2)灵活运用运算律;
(3)运算结果要化简,使结果为最简分式或整式.
2.分式加减在实际问题中的应用. 顽强的毅力可以征服世界上任何一座高峰!
—— 狄更斯
