3.2.2双曲线的简单几何性质课件(第3课时) 课件(共20张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质课件(第3课时) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 656.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 21:03:03 | ||
图片预览







文档简介
(共20张PPT)
第 3 章圆锥曲线的方程
3.2.2 双曲线的简单几何性质
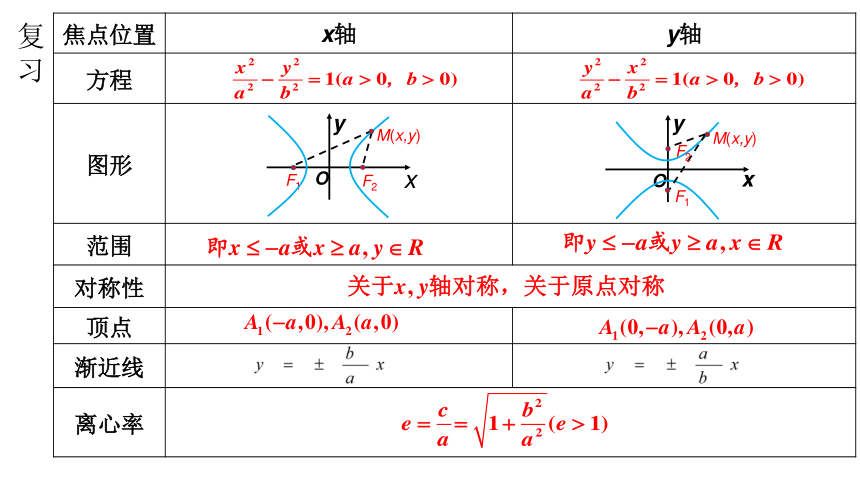
焦点位置 x轴 y轴
方程
图形
范围
对称性 顶点
渐近线
离心率 x
F1
F2
y
O
M(x,y)
x
y
O
M(x,y)
F1
F2
复习
p
p
练习1.已知双曲线C:x2-=1和点P(1,2),判断它们两者之间的关系?
1.相离:
2.相切:
3.相交:
直线与椭圆组成的方程组无解
直线与椭圆组成的方程组只有一组解
直线与椭圆组成的方程组有两组解
当Δ>0时,方程有两解,直线与椭圆相交;
当Δ=0时,方程有一解,直线与椭圆相切;
当Δ<0时,方程无解 ,直线与椭圆相离.
复习.
Δ>0 相交,两个交点
Δ=0 相切,一个交点
Δ<0 相离,无交点
(b2-a2k2)x2-2a2mkx-a2m2-a2b2=0
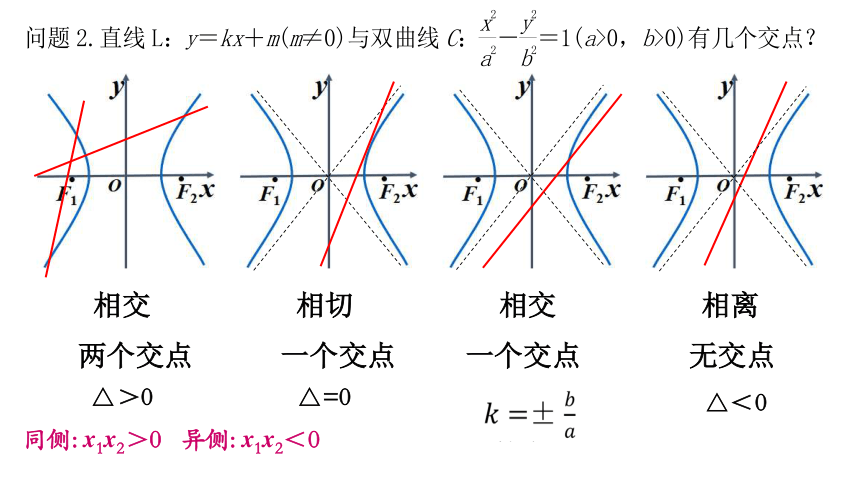
相交
相交
相切
相离
两个交点
一个交点
一个交点
无交点
△>0
△=0
△<0
同侧: x1x2>0 异侧: x1x2<0
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(1)若直线l与双曲线C有2个公共点,求k的取值范围;
(2)若直线l与双曲线C只有1个公共点,求k的取值范围;
(3)若直线l与双曲线C的右支有2个公共点,求k的取值范围.
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(1)若直线l与双曲线C有2个公共点,求k的取值范围;
解:联立直线与双曲线的方程
消去y,得
因为直线与双曲线有两个公共点,
所以解得
所以
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(2)若直线l与双曲线C只有1个公共点,求k的取值范围;
解:
消去y,得
当1-k2≠0即k≠±1时,若直线与双曲线只有一个公共点
则
即
当1-k2=0即k=±1时,方程只有一个解,
即直线与双曲线只有一个公共点;
综上,
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(3)若直线l与双曲线C的右支有2个公共点,求k的取值范围.
解:
消去y,得
因为直线l与双曲线C的右支有2个公共点,
所以
解得
练习2 直线l:y=kx-1与双曲线C:x2-y2=1的左支有两个公共点,则k的取值范围( )
A. (,0) B.(,) C.(,1) D.1)
C
解:
整理得
根据题意
解得
例2
F2
O
x
y
A
B
F1
例2
F2
O
x
y
A
B
F1
练习3.已知直线y=4x-6与双曲线 相交于A,B两点,求线段AB的长度.
解:联立直线与双曲线的方程
消去y,得
所以
所以
例3.已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
解: 法一:由题意知直线的斜率存在,
故可设直线方程为y+1=k(x-3),即y=kx-3k-1,联立双曲线
消去y,整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),∴x1+x2=.
∵A(3,-1)为MN的中点,∴=3,即=6,解得k=-.
∴所求直线MN的方程为y=-x+,即3x+4y-5=0.
例3.已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
法二:设M(x1,y1),N(x2,y2),∵M,N均在双曲线上,
∴-y12=1,-y22=1 ,
两式相减得=.∵点A平分弦MN,
∴x1+x2=6,y1+y2=-2. ∴kMN==-.
∴所求直线MN的方程为y+1=-(x-3),即3x+4y-5=0.
第 3 章圆锥曲线的方程
3.2.2 双曲线的简单几何性质
焦点位置 x轴 y轴
方程
图形
范围
对称性 顶点
渐近线
离心率 x
F1
F2
y
O
M(x,y)
x
y
O
M(x,y)
F1
F2
复习
p
p
练习1.已知双曲线C:x2-=1和点P(1,2),判断它们两者之间的关系?
1.相离:
2.相切:
3.相交:
直线与椭圆组成的方程组无解
直线与椭圆组成的方程组只有一组解
直线与椭圆组成的方程组有两组解
当Δ>0时,方程有两解,直线与椭圆相交;
当Δ=0时,方程有一解,直线与椭圆相切;
当Δ<0时,方程无解 ,直线与椭圆相离.
复习.
Δ>0 相交,两个交点
Δ=0 相切,一个交点
Δ<0 相离,无交点
(b2-a2k2)x2-2a2mkx-a2m2-a2b2=0
相交
相交
相切
相离
两个交点
一个交点
一个交点
无交点
△>0
△=0
△<0
同侧: x1x2>0 异侧: x1x2<0
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(1)若直线l与双曲线C有2个公共点,求k的取值范围;
(2)若直线l与双曲线C只有1个公共点,求k的取值范围;
(3)若直线l与双曲线C的右支有2个公共点,求k的取值范围.
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(1)若直线l与双曲线C有2个公共点,求k的取值范围;
解:联立直线与双曲线的方程
消去y,得
因为直线与双曲线有两个公共点,
所以解得
所以
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(2)若直线l与双曲线C只有1个公共点,求k的取值范围;
解:
消去y,得
当1-k2≠0即k≠±1时,若直线与双曲线只有一个公共点
则
即
当1-k2=0即k=±1时,方程只有一个解,
即直线与双曲线只有一个公共点;
综上,
例1 已知双曲线C:x2-y2=4,直线l:y=kx-1.
(3)若直线l与双曲线C的右支有2个公共点,求k的取值范围.
解:
消去y,得
因为直线l与双曲线C的右支有2个公共点,
所以
解得
练习2 直线l:y=kx-1与双曲线C:x2-y2=1的左支有两个公共点,则k的取值范围( )
A. (,0) B.(,) C.(,1) D.1)
C
解:
整理得
根据题意
解得
例2
F2
O
x
y
A
B
F1
例2
F2
O
x
y
A
B
F1
练习3.已知直线y=4x-6与双曲线 相交于A,B两点,求线段AB的长度.
解:联立直线与双曲线的方程
消去y,得
所以
所以
例3.已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
解: 法一:由题意知直线的斜率存在,
故可设直线方程为y+1=k(x-3),即y=kx-3k-1,联立双曲线
消去y,整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),∴x1+x2=.
∵A(3,-1)为MN的中点,∴=3,即=6,解得k=-.
∴所求直线MN的方程为y=-x+,即3x+4y-5=0.
例3.已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
法二:设M(x1,y1),N(x2,y2),∵M,N均在双曲线上,
∴-y12=1,-y22=1 ,
两式相减得=.∵点A平分弦MN,
∴x1+x2=6,y1+y2=-2. ∴kMN==-.
∴所求直线MN的方程为y+1=-(x-3),即3x+4y-5=0.
