第26章 反比例函数单元测试题(含解析)
文档属性
| 名称 | 第26章 反比例函数单元测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 250.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 20:57:03 | ||
图片预览




文档简介
2023-2024学年人教版九年级数学下册 第26章 反比例函数 单元测试题
一、选择题(共10题;共30分)
1.(3分)当三角形的面积一定时,三角形的底和底边上的高成( )关系.
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
2.(3分)在下列函数中,y是x的反比例函数的是( )
A.y=x-1 B.y= C.y=-2x-1 D. =2
3.(3分)点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数的图象上,则y1、y2、y3,的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
4.(3分)如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数,在第一象限内的图像交于点B,连接,若,,则m的值是( )
A.6 B.8 C.10 D.12
5.(3分)某市举行中学生数学知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是( ).
A.甲 B.乙 C.丙 D.丁
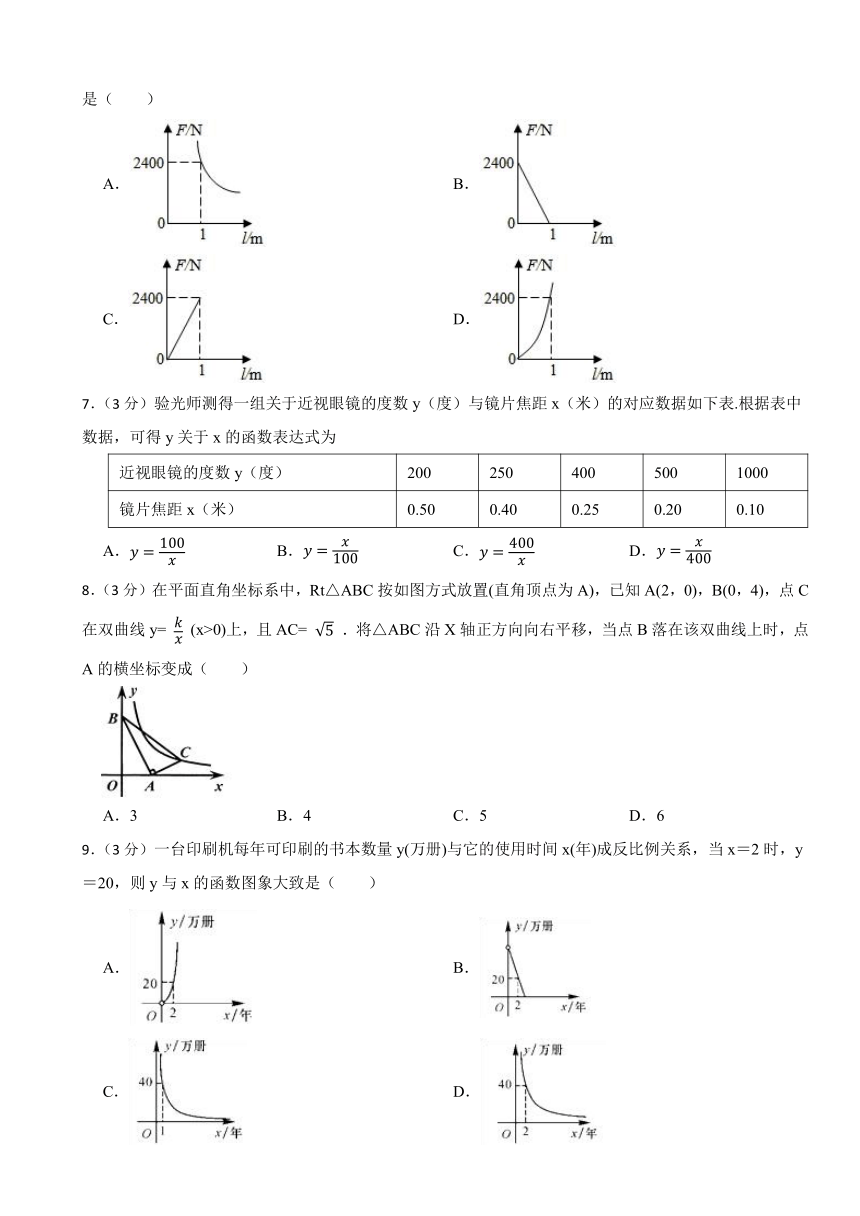
6.(3分)小明学习了物理中的杠杆平衡原理发现:阻力 阻力臂 动力 动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力 (单位:N)关于动力臂 (单位:m)的函数图象大致是( )
A. B.
C. D.
7.(3分)验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
8.(3分)在平面直角坐标系中,Rt△ABC按如图方式放置(直角顶点为A),已知A(2,0),B(0,4),点C在双曲线y= (x>0)上,且AC= .将△ABC沿X轴正方向向右平移,当点B落在该双曲线上时,点A的横坐标变成( )
A.3 B.4 C.5 D.6
9.(3分)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20,则y与x的函数图象大致是( )
A. B.
C. D.
10.(3分)如图,点A是反比例函数y=是图象上一点,AB⊥y轴于点B,则△AOB的面积是( )
A.1 B.2 C.3 D.4
二、填空题(共8题;共24分)
11.(3分)已知,则 .
12.(3分)如果函数y=(m﹣1) 是反比例函数,那么m的值是 .
13.(3分)若反比例函数y= 的图象位于一、三象限内,则k的取值范围是 .
14.(3分)若点,,都在反比例函数的图象上,则,,的大小关系是 .
15.(3分)如图,在平面直角坐标系中,点是轴上任意一点,轴,分别交,的图象于两点,若的面积是,则的值为 .
16.(3分)密闭容器内有一定质量的二氧化碳,在温度不变的情况下,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ是体积V的反比例函数关系,它的图象如图所示,则当ρ = 3.3 kg/m3时,相应的体积V是 m3.
17.(3分)我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b的反比例函数,其函数关系式可以写为a= (S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例: ;函数关系式: .
18.(3分)一定质量的二氧化碳,其体积V(m3)是密度ρ(kg/m3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=1.9m3时,ρ= .
三、解答题(共8题;共66分)
19.(6分)已知y是x的反比例函数,且当x=2时,y=﹣3,请你确定该反比例函数的解析式,并求当y=6时,自变量x的值.
20.(6分)若反比例函数y= 的图象经过第二、四象限,求函数的解析式.
21.(7分)如图,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.求△ABC的面积.
22.(7分)已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
23.(8分)某乡要在生活垃圾存放区建一个老年活动中心,这样必须把1 200 m3的生活垃圾运走.
(1)假如每天能运x m3,所需时间为y天,写出y与x之间的函数关系式;
(2)若每辆拖拉机一天能运12 m3,则5辆这样的拖拉机要多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
24.(8分)如图,一次函数的图像与x轴、y轴分别交于A,B两点,与反比例函数的图像分别交于C,D两点,已知点C的坐标是,且,求一次函数与反比例函数的解析式.
25.(12分)如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,BN于C,设AD=x,BC=y,求y与x的函数关系式.
26.(12分)某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)(6分)求甲、乙两种品牌空调的进货价;
(2)(6分)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
答案解析部分
1.【答案】B
【知识点】反比例函数的定义
【解析】【解答】解:三角形的底×高=三角形面积×2(定值),
即三角形的底和高成反比例.
故选B.
【分析】由于三角形面积= ×底×高,所以面积一定时,底×高=定值,即底和高成反比例.
2.【答案】C
【知识点】反比例函数的定义
【解析】【解答】解:反比例函数的定义是:“形如 的函数叫做反比例函数”,其表达形式一般有3种,分别为:① ;② ;③ ,上述四个选项中,只有C选项中的式子符合要求,故答案为:C.
【分析】根据反比例函数的定义是:“形如 的函数叫做反比例函数”和其表达形式"① ;② ;③"并结合各选项可判断求解.
3.【答案】D
【知识点】反比例函数的性质
【解析】【解答】解:∵y=,
∴反比例函数的图象位于二、四象限,且在每一象限内,y随x的增大而增大,
∴A (-2,y1)、B(-1,y2)位于第二象限,C(3,y3)位于第四象限.
∵-2<-1,
∴y3<y1<y2.
故答案为:D.
【分析】由反比例函数的性质可得:其图象位于二、四象限,且在每一象限内,y随x的增大而增大,据此进行比较.
4.【答案】D
【知识点】反比例函数的图象;三角形的面积;锐角三角函数的定义
【解析】【解答】解:过点B作BD⊥y轴于点D,
令y=kx+4中的x=0,得y=4,
∴C(0,4),
∴OC=4.
∵S△OBC=4,
∴OC·BD=4,
∴BD=2.
∵tan∠BOC=,
∴OD=6,
∴B(2,6).
∵点B在反比例函数y=的图象上,
∴m=2×6=12.
故答案为:D.
【分析】过点B作BD⊥y轴于点D,易得C(0,4),则OC=4,根据三角形的面积公式可得BD的值,利用三角函数的概念可得OD,据此可得点B的坐标,然后代入y=中就可求出m的值.
5.【答案】C
【知识点】反比例函数的实际应用
【解析】【解答】解:∵用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,
∴xy的值就是该校的优秀人数,
∵描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两所学校的优秀人数相等,
点丙在反比例函数图象的上方,
∴丙的优秀人数最多.
故答案为:C
【分析】观察图象可知xy的值就是该校的优秀人数,乙、丁两所学校的优秀人数相等;点丙在反比例函数图象的上方,据此可得到丙的优秀人数最多.
6.【答案】A
【知识点】反比例函数的图象;反比例函数的实际应用
【解析】【解答】解:∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是2400N和1m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:2400×1=Fl,
则F= ,是反比例函数,A选项符合,
故答案为:A.
【分析】利用阻力×阻力臂=动力×动力臂,将已知数据代入得出函数关系式,从而确定其图象即可.
7.【答案】A
【知识点】列反比例函数关系式
【解析】【解答】解:由表格中数据可得:xy=100,
故y关于x的函数表达式为:.
故答案为:A.
【分析】由表格中数据可得:xy=100,变形即可得到y关于x的函数表达式.
8.【答案】A
【知识点】反比例函数的实际应用;勾股定理;坐标与图形变化﹣平移;相似三角形的判定与性质
【解析】【解答】过C作CD⊥x轴于D,
∵A(2,0),B(0,4)
∴OA=2,OB=4
∵∠ADC=90 ,
∴∠DAC+∠ACD=90 ,
∵∠BAC=90 ,
∴∠DAC+∠BAO=90 ,
∴∠ACD=∠BAO,
∵∠BOA=∠ADC=90 ,
∴△BOA∽△ADC,
∴
设DC=x,则AD=2x,
∵AC=,
∴x2+(2x)2=()2,
x1=1,x2= 1(舍),
∴AD=2,DC=1,
∴OD=OA+AD=4
∴C(4,1),
∴k=1×4=4,
当y=4时,x=1,即△ABC向右平移1个单位时,点B落在该双曲线上,
∴点A的横坐标为3;
故选:A.
【分析】根据点A、B的坐标求出OA、OB的长,再根据已知证明△BOA∽△ADC,得出对应边成比例,从而可求出AD=2DC,在Rt△ADC中,利用勾股定理求出AD、DC的长,可得出点C的坐标,根据点B的坐标为(0,4),再求出当y=4时x=1,(4,1)这点在双曲线上,因此可得出△ABC向右平移1个单位时,点B落在该双曲线上,继而得出点A的横坐标。
9.【答案】C
【知识点】反比例函数的实际应用
【解析】【解答】解:设y= (k≠0),
∵当x=2时,y=20,
∴k=40,
∴y= ,
则y与x的函数图象大致是C,
故答案为:C.
【分析】设y=(k≠0),根据当x=2时,y=20,求出k,即可得出y与x的函数图象.
10.【答案】B
【知识点】列反比例函数关系式
【解析】【解答】解:由题意得:点A是反比例函数y=图象上一点,S△AOB==2.
故选B.
【分析】此题可从反比例函数系数k的几何意义入手,△AOB的面积为点A向两条坐标轴作垂线,与坐标轴围成的矩形面积的一半即S=.
11.【答案】1
【知识点】反比例函数的定义
【解析】【解答】解:当时,
故答案为:1
【分析】已知f(x),代入求值即可。
12.【答案】﹣1
【知识点】反比例函数的定义
【解析】【解答】解:根据题意m2﹣2=﹣1,
m=±1,
又m﹣1≠0,m≠1,
所以m=﹣1.
故答案为:﹣1.
【分析】根据反比例函数的定义可得m2﹣2=﹣1,且m﹣1≠0,从而求出m的值.
13.【答案】k>3
【知识点】反比例函数的性质
【解析】【解答】解:由于反比例函数y= 的图象位于第一、三象限,
则k﹣3>0,解得:k>3.
故答案为:k>3.
【分析】由题意得,反比例函数经过一、三象限,则k﹣3>0,求出k的取值范围即可.
14.【答案】
【知识点】反比例函数图象上点的坐标特征
【解析】【解答】解:点A(x1,2)在反比例函数的图象上,
∴2x1=8,
解得x1=4;
点B(x2,-1)在反比例函数的图象上,
∴-x2=8,
解得x2=-8;
点C(x3,4)在反比例函数的图象上,
∴4x3=8,
解得x3=2;
∴x1>x3>x2.
故答案为:x1>x3>x2.
【分析】根据反比例函数图象上任意一点的横纵坐标的乘积等于比例系数k可求出x1、x2与x3的值,从而即可比较大小得出答案.
15.【答案】
【知识点】反比例函数系数k的几何意义;三角形的面积
【解析】【解答】解:连接OB、OC,
∵BC∥x轴,
∴S△ACB=S△OCB,
∴×|2|+|k|=3,
∴k=±4.
∵k<0,
∴k=-4.
故答案为:-4.
【分析】连接OB、OC,根据等底等高的三角形面积相等可得S△ACB=S△OCB,由反比例函数系数k的几何意义可得S△OCB=×|2|+|k|=3,求解即可.
16.【答案】3
【知识点】反比例函数的实际应用
【解析】【解答】解:设密度ρ与体积V的反比例函数解析式为ρ=,
把点(5,1.98)代入解ρ=,得k=9.9,
∴密度ρ与体积V的反比例函数解析式为ρ=,V>0.
当ρ = 3.3时,V==3,
即当ρ = 3.3 kg/m3时,相应的体积V是 3m3.
故答案为:3.
【分析】设密度ρ与体积V的反比例函数解析式为ρ=,把点(5,1.98)代入求出k的值,据此可得函数解析式,然后令ρ=3.3,求出V的值即可.
17.【答案】当路程s一定时,速度v是时间t的反比例函数;函数关系式为:v= (s为常数).(答案不唯一)
【知识点】列反比例函数关系式
【解析】【解答】解:当路程s一定时,速度v是时间t的反比例函数;函数关系式为:v= (s为常数).答案不唯一.
【分析】根据题意结合实际情况来写出.
18.【答案】5kg/m3
【知识点】反比例函数的实际应用
【解析】【解答】解:设函数关系式为:V= ,由图象可得:V=5,ρ=1.9,代入得:
k=5×1.9=9.5,
故V= ,
当V=1.9时,ρ=5kg/m3.
故答案为:5kg/m3.
【分析】由图象可得k=9.5,进而得出V=1.9m3时,ρ的值.
19.【答案】解:设反比例函数y= (k≠0),
∵当x=2时,y=﹣3,
∴k=xy=2×(﹣3)=﹣6,
∴y与x之间的函数关系式y=﹣ .
把y=6代入y=﹣ ,则x=﹣1
【知识点】反比例函数的定义;反比例函数的性质
【解析】【分析】由题意y是x的反比例函数,可设y= (k≠0),然后利用待定系数法进行求解;把y=6代入函数解析式求得相应的x的值即可.
20.【答案】解:根据题意得: ,
解得:m=﹣5
则函数的解析式是:y=﹣
【知识点】反比例函数的定义;反比例函数的性质
【解析】【分析】根据反比例函数的定义,可以得到m2﹣24=1,而图象经过第二、四象限,则比例系数是负数,据此即可求解.
21.【答案】解:∵,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.
∴A(3,3),B(1,1),
∴OA=AC=3 ,OB= ,
∴AB=3 ﹣ =2 ,
∴S= AB AC= ×2 ×3 =6
【知识点】反比例函数系数k的几何意义;等腰直角三角形
【解析】【分析】根据等腰直角三角形的性质已结反比例函数系数k的几何意义求得A(3,3),B(1,1),进而根据勾股定理求得OA=AC=3 ,OB= ,然后根据三角形面积公式即可求得.
22.【答案】解:∵y1与x成正比例,∴y1=kx,∵y2与x+2成反比例,∴y2= ,∵y=y1+y2,∴y=kx+ ,∵当x=﹣1时,y=3;当x=3时,y=7,∴ ,解得: ,∴y=2x+ ,当x=﹣3时,y=2×(﹣3)﹣5=﹣11
【知识点】反比例函数的定义;正比例函数的定义
【解析】【分析】首先设出y1=kx, 再将它们代入y=y1+y2,然后用待定系数法即可求出y关于x的函数关系式;最后把x=﹣3代入求值即可。
23.【答案】解:(1)每天运量x m3时,需时间y=天;
(2)5辆拖拉机每天能运5×12 m3=60 m3,则y=1 200÷60=20,即需要20天运完;
(3)假设需要增加n辆,根据题意:8×60+6×12(n+5)≥1 200,n≥5
答:(1) 天(2)要20天才能完成;(3)至少需要增加5辆.
【知识点】反比例函数的性质;列反比例函数关系式
【解析】【分析】根据实际问题列反比例函数关系式。
24.【答案】解:∵点在反比例函数的图像上,
∴,
∴,
过点C作轴于点M,
∵,,
∴,
∴,
∵,
∴,,
∵,
∴,
∴,
即,
∴,,
∴点A,B的坐标分别为,,
∵一次函数的解析式为:,根据题意可得:
∴,
解得,
∴.
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
【解析】【分析】 将点C的坐标代入求出k的值,过点C作轴于点M, 先证出,可得,再将数据代入求出,,再利用待定系数法求出一次函数解析式即可。
25.【答案】解:作DF⊥BN交BC于F;
∵AM、BN与⊙O切于点定A、B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BC﹣BF=y﹣x;
∵DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(y﹣x)2+122,
整理为,
∴y与x的函数关系式是.
【知识点】列反比例函数关系式
【解析】【分析】根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系.
26.【答案】(1)解:由(1)设甲种品牌的进价为x元,则乙种品牌空调的进价为(1+20%)x元,
由题意,得 ,
解得x=1500,
经检验,x=1500是原分式方程的解.
乙种品牌空调的进价为(1+20%)×1500=1800(元).
答案:甲种品牌的进价为1500元,乙种品牌空调的进价为1800元.
(2)解:设购进甲种品牌空调a台,则购进乙种品牌空调(10-a)台,
由题意,得1500a+1800(10-a)≤16000,
解得 ≤a,
设利润为w,则w=(2500-1500)a+(3500-1800)(10-a)=-700a+17000,
因为-700<0,则w随a的增大而减少,当a=7时,w最大,最大为12100元.
答:当购进甲种品牌空调7台,乙种品牌空调3台时,售完后利润最大,最大为12100元.
【知识点】反比例函数的实际应用
【解析】【分析】(1)列分式方程解答,可设甲种品牌的进价为x元,数量关系: ;(2)设购进甲种品牌空调a台,先根据“成本价”求出a的取值范围;再用含a的代数式表示利润的式子,并分析最值.
一、选择题(共10题;共30分)
1.(3分)当三角形的面积一定时,三角形的底和底边上的高成( )关系.
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
2.(3分)在下列函数中,y是x的反比例函数的是( )
A.y=x-1 B.y= C.y=-2x-1 D. =2
3.(3分)点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数的图象上,则y1、y2、y3,的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
4.(3分)如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数,在第一象限内的图像交于点B,连接,若,,则m的值是( )
A.6 B.8 C.10 D.12
5.(3分)某市举行中学生数学知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是( ).
A.甲 B.乙 C.丙 D.丁
6.(3分)小明学习了物理中的杠杆平衡原理发现:阻力 阻力臂 动力 动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力 (单位:N)关于动力臂 (单位:m)的函数图象大致是( )
A. B.
C. D.
7.(3分)验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
8.(3分)在平面直角坐标系中,Rt△ABC按如图方式放置(直角顶点为A),已知A(2,0),B(0,4),点C在双曲线y= (x>0)上,且AC= .将△ABC沿X轴正方向向右平移,当点B落在该双曲线上时,点A的横坐标变成( )
A.3 B.4 C.5 D.6
9.(3分)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20,则y与x的函数图象大致是( )
A. B.
C. D.
10.(3分)如图,点A是反比例函数y=是图象上一点,AB⊥y轴于点B,则△AOB的面积是( )
A.1 B.2 C.3 D.4
二、填空题(共8题;共24分)
11.(3分)已知,则 .
12.(3分)如果函数y=(m﹣1) 是反比例函数,那么m的值是 .
13.(3分)若反比例函数y= 的图象位于一、三象限内,则k的取值范围是 .
14.(3分)若点,,都在反比例函数的图象上,则,,的大小关系是 .
15.(3分)如图,在平面直角坐标系中,点是轴上任意一点,轴,分别交,的图象于两点,若的面积是,则的值为 .
16.(3分)密闭容器内有一定质量的二氧化碳,在温度不变的情况下,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ是体积V的反比例函数关系,它的图象如图所示,则当ρ = 3.3 kg/m3时,相应的体积V是 m3.
17.(3分)我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b的反比例函数,其函数关系式可以写为a= (S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例: ;函数关系式: .
18.(3分)一定质量的二氧化碳,其体积V(m3)是密度ρ(kg/m3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=1.9m3时,ρ= .
三、解答题(共8题;共66分)
19.(6分)已知y是x的反比例函数,且当x=2时,y=﹣3,请你确定该反比例函数的解析式,并求当y=6时,自变量x的值.
20.(6分)若反比例函数y= 的图象经过第二、四象限,求函数的解析式.
21.(7分)如图,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.求△ABC的面积.
22.(7分)已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
23.(8分)某乡要在生活垃圾存放区建一个老年活动中心,这样必须把1 200 m3的生活垃圾运走.
(1)假如每天能运x m3,所需时间为y天,写出y与x之间的函数关系式;
(2)若每辆拖拉机一天能运12 m3,则5辆这样的拖拉机要多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
24.(8分)如图,一次函数的图像与x轴、y轴分别交于A,B两点,与反比例函数的图像分别交于C,D两点,已知点C的坐标是,且,求一次函数与反比例函数的解析式.
25.(12分)如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,BN于C,设AD=x,BC=y,求y与x的函数关系式.
26.(12分)某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)(6分)求甲、乙两种品牌空调的进货价;
(2)(6分)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
答案解析部分
1.【答案】B
【知识点】反比例函数的定义
【解析】【解答】解:三角形的底×高=三角形面积×2(定值),
即三角形的底和高成反比例.
故选B.
【分析】由于三角形面积= ×底×高,所以面积一定时,底×高=定值,即底和高成反比例.
2.【答案】C
【知识点】反比例函数的定义
【解析】【解答】解:反比例函数的定义是:“形如 的函数叫做反比例函数”,其表达形式一般有3种,分别为:① ;② ;③ ,上述四个选项中,只有C选项中的式子符合要求,故答案为:C.
【分析】根据反比例函数的定义是:“形如 的函数叫做反比例函数”和其表达形式"① ;② ;③"并结合各选项可判断求解.
3.【答案】D
【知识点】反比例函数的性质
【解析】【解答】解:∵y=,
∴反比例函数的图象位于二、四象限,且在每一象限内,y随x的增大而增大,
∴A (-2,y1)、B(-1,y2)位于第二象限,C(3,y3)位于第四象限.
∵-2<-1,
∴y3<y1<y2.
故答案为:D.
【分析】由反比例函数的性质可得:其图象位于二、四象限,且在每一象限内,y随x的增大而增大,据此进行比较.
4.【答案】D
【知识点】反比例函数的图象;三角形的面积;锐角三角函数的定义
【解析】【解答】解:过点B作BD⊥y轴于点D,
令y=kx+4中的x=0,得y=4,
∴C(0,4),
∴OC=4.
∵S△OBC=4,
∴OC·BD=4,
∴BD=2.
∵tan∠BOC=,
∴OD=6,
∴B(2,6).
∵点B在反比例函数y=的图象上,
∴m=2×6=12.
故答案为:D.
【分析】过点B作BD⊥y轴于点D,易得C(0,4),则OC=4,根据三角形的面积公式可得BD的值,利用三角函数的概念可得OD,据此可得点B的坐标,然后代入y=中就可求出m的值.
5.【答案】C
【知识点】反比例函数的实际应用
【解析】【解答】解:∵用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,
∴xy的值就是该校的优秀人数,
∵描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两所学校的优秀人数相等,
点丙在反比例函数图象的上方,
∴丙的优秀人数最多.
故答案为:C
【分析】观察图象可知xy的值就是该校的优秀人数,乙、丁两所学校的优秀人数相等;点丙在反比例函数图象的上方,据此可得到丙的优秀人数最多.
6.【答案】A
【知识点】反比例函数的图象;反比例函数的实际应用
【解析】【解答】解:∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是2400N和1m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:2400×1=Fl,
则F= ,是反比例函数,A选项符合,
故答案为:A.
【分析】利用阻力×阻力臂=动力×动力臂,将已知数据代入得出函数关系式,从而确定其图象即可.
7.【答案】A
【知识点】列反比例函数关系式
【解析】【解答】解:由表格中数据可得:xy=100,
故y关于x的函数表达式为:.
故答案为:A.
【分析】由表格中数据可得:xy=100,变形即可得到y关于x的函数表达式.
8.【答案】A
【知识点】反比例函数的实际应用;勾股定理;坐标与图形变化﹣平移;相似三角形的判定与性质
【解析】【解答】过C作CD⊥x轴于D,
∵A(2,0),B(0,4)
∴OA=2,OB=4
∵∠ADC=90 ,
∴∠DAC+∠ACD=90 ,
∵∠BAC=90 ,
∴∠DAC+∠BAO=90 ,
∴∠ACD=∠BAO,
∵∠BOA=∠ADC=90 ,
∴△BOA∽△ADC,
∴
设DC=x,则AD=2x,
∵AC=,
∴x2+(2x)2=()2,
x1=1,x2= 1(舍),
∴AD=2,DC=1,
∴OD=OA+AD=4
∴C(4,1),
∴k=1×4=4,
当y=4时,x=1,即△ABC向右平移1个单位时,点B落在该双曲线上,
∴点A的横坐标为3;
故选:A.
【分析】根据点A、B的坐标求出OA、OB的长,再根据已知证明△BOA∽△ADC,得出对应边成比例,从而可求出AD=2DC,在Rt△ADC中,利用勾股定理求出AD、DC的长,可得出点C的坐标,根据点B的坐标为(0,4),再求出当y=4时x=1,(4,1)这点在双曲线上,因此可得出△ABC向右平移1个单位时,点B落在该双曲线上,继而得出点A的横坐标。
9.【答案】C
【知识点】反比例函数的实际应用
【解析】【解答】解:设y= (k≠0),
∵当x=2时,y=20,
∴k=40,
∴y= ,
则y与x的函数图象大致是C,
故答案为:C.
【分析】设y=(k≠0),根据当x=2时,y=20,求出k,即可得出y与x的函数图象.
10.【答案】B
【知识点】列反比例函数关系式
【解析】【解答】解:由题意得:点A是反比例函数y=图象上一点,S△AOB==2.
故选B.
【分析】此题可从反比例函数系数k的几何意义入手,△AOB的面积为点A向两条坐标轴作垂线,与坐标轴围成的矩形面积的一半即S=.
11.【答案】1
【知识点】反比例函数的定义
【解析】【解答】解:当时,
故答案为:1
【分析】已知f(x),代入求值即可。
12.【答案】﹣1
【知识点】反比例函数的定义
【解析】【解答】解:根据题意m2﹣2=﹣1,
m=±1,
又m﹣1≠0,m≠1,
所以m=﹣1.
故答案为:﹣1.
【分析】根据反比例函数的定义可得m2﹣2=﹣1,且m﹣1≠0,从而求出m的值.
13.【答案】k>3
【知识点】反比例函数的性质
【解析】【解答】解:由于反比例函数y= 的图象位于第一、三象限,
则k﹣3>0,解得:k>3.
故答案为:k>3.
【分析】由题意得,反比例函数经过一、三象限,则k﹣3>0,求出k的取值范围即可.
14.【答案】
【知识点】反比例函数图象上点的坐标特征
【解析】【解答】解:点A(x1,2)在反比例函数的图象上,
∴2x1=8,
解得x1=4;
点B(x2,-1)在反比例函数的图象上,
∴-x2=8,
解得x2=-8;
点C(x3,4)在反比例函数的图象上,
∴4x3=8,
解得x3=2;
∴x1>x3>x2.
故答案为:x1>x3>x2.
【分析】根据反比例函数图象上任意一点的横纵坐标的乘积等于比例系数k可求出x1、x2与x3的值,从而即可比较大小得出答案.
15.【答案】
【知识点】反比例函数系数k的几何意义;三角形的面积
【解析】【解答】解:连接OB、OC,
∵BC∥x轴,
∴S△ACB=S△OCB,
∴×|2|+|k|=3,
∴k=±4.
∵k<0,
∴k=-4.
故答案为:-4.
【分析】连接OB、OC,根据等底等高的三角形面积相等可得S△ACB=S△OCB,由反比例函数系数k的几何意义可得S△OCB=×|2|+|k|=3,求解即可.
16.【答案】3
【知识点】反比例函数的实际应用
【解析】【解答】解:设密度ρ与体积V的反比例函数解析式为ρ=,
把点(5,1.98)代入解ρ=,得k=9.9,
∴密度ρ与体积V的反比例函数解析式为ρ=,V>0.
当ρ = 3.3时,V==3,
即当ρ = 3.3 kg/m3时,相应的体积V是 3m3.
故答案为:3.
【分析】设密度ρ与体积V的反比例函数解析式为ρ=,把点(5,1.98)代入求出k的值,据此可得函数解析式,然后令ρ=3.3,求出V的值即可.
17.【答案】当路程s一定时,速度v是时间t的反比例函数;函数关系式为:v= (s为常数).(答案不唯一)
【知识点】列反比例函数关系式
【解析】【解答】解:当路程s一定时,速度v是时间t的反比例函数;函数关系式为:v= (s为常数).答案不唯一.
【分析】根据题意结合实际情况来写出.
18.【答案】5kg/m3
【知识点】反比例函数的实际应用
【解析】【解答】解:设函数关系式为:V= ,由图象可得:V=5,ρ=1.9,代入得:
k=5×1.9=9.5,
故V= ,
当V=1.9时,ρ=5kg/m3.
故答案为:5kg/m3.
【分析】由图象可得k=9.5,进而得出V=1.9m3时,ρ的值.
19.【答案】解:设反比例函数y= (k≠0),
∵当x=2时,y=﹣3,
∴k=xy=2×(﹣3)=﹣6,
∴y与x之间的函数关系式y=﹣ .
把y=6代入y=﹣ ,则x=﹣1
【知识点】反比例函数的定义;反比例函数的性质
【解析】【分析】由题意y是x的反比例函数,可设y= (k≠0),然后利用待定系数法进行求解;把y=6代入函数解析式求得相应的x的值即可.
20.【答案】解:根据题意得: ,
解得:m=﹣5
则函数的解析式是:y=﹣
【知识点】反比例函数的定义;反比例函数的性质
【解析】【分析】根据反比例函数的定义,可以得到m2﹣24=1,而图象经过第二、四象限,则比例系数是负数,据此即可求解.
21.【答案】解:∵,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.
∴A(3,3),B(1,1),
∴OA=AC=3 ,OB= ,
∴AB=3 ﹣ =2 ,
∴S= AB AC= ×2 ×3 =6
【知识点】反比例函数系数k的几何意义;等腰直角三角形
【解析】【分析】根据等腰直角三角形的性质已结反比例函数系数k的几何意义求得A(3,3),B(1,1),进而根据勾股定理求得OA=AC=3 ,OB= ,然后根据三角形面积公式即可求得.
22.【答案】解:∵y1与x成正比例,∴y1=kx,∵y2与x+2成反比例,∴y2= ,∵y=y1+y2,∴y=kx+ ,∵当x=﹣1时,y=3;当x=3时,y=7,∴ ,解得: ,∴y=2x+ ,当x=﹣3时,y=2×(﹣3)﹣5=﹣11
【知识点】反比例函数的定义;正比例函数的定义
【解析】【分析】首先设出y1=kx, 再将它们代入y=y1+y2,然后用待定系数法即可求出y关于x的函数关系式;最后把x=﹣3代入求值即可。
23.【答案】解:(1)每天运量x m3时,需时间y=天;
(2)5辆拖拉机每天能运5×12 m3=60 m3,则y=1 200÷60=20,即需要20天运完;
(3)假设需要增加n辆,根据题意:8×60+6×12(n+5)≥1 200,n≥5
答:(1) 天(2)要20天才能完成;(3)至少需要增加5辆.
【知识点】反比例函数的性质;列反比例函数关系式
【解析】【分析】根据实际问题列反比例函数关系式。
24.【答案】解:∵点在反比例函数的图像上,
∴,
∴,
过点C作轴于点M,
∵,,
∴,
∴,
∵,
∴,,
∵,
∴,
∴,
即,
∴,,
∴点A,B的坐标分别为,,
∵一次函数的解析式为:,根据题意可得:
∴,
解得,
∴.
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
【解析】【分析】 将点C的坐标代入求出k的值,过点C作轴于点M, 先证出,可得,再将数据代入求出,,再利用待定系数法求出一次函数解析式即可。
25.【答案】解:作DF⊥BN交BC于F;
∵AM、BN与⊙O切于点定A、B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BC﹣BF=y﹣x;
∵DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(y﹣x)2+122,
整理为,
∴y与x的函数关系式是.
【知识点】列反比例函数关系式
【解析】【分析】根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系.
26.【答案】(1)解:由(1)设甲种品牌的进价为x元,则乙种品牌空调的进价为(1+20%)x元,
由题意,得 ,
解得x=1500,
经检验,x=1500是原分式方程的解.
乙种品牌空调的进价为(1+20%)×1500=1800(元).
答案:甲种品牌的进价为1500元,乙种品牌空调的进价为1800元.
(2)解:设购进甲种品牌空调a台,则购进乙种品牌空调(10-a)台,
由题意,得1500a+1800(10-a)≤16000,
解得 ≤a,
设利润为w,则w=(2500-1500)a+(3500-1800)(10-a)=-700a+17000,
因为-700<0,则w随a的增大而减少,当a=7时,w最大,最大为12100元.
答:当购进甲种品牌空调7台,乙种品牌空调3台时,售完后利润最大,最大为12100元.
【知识点】反比例函数的实际应用
【解析】【分析】(1)列分式方程解答,可设甲种品牌的进价为x元,数量关系: ;(2)设购进甲种品牌空调a台,先根据“成本价”求出a的取值范围;再用含a的代数式表示利润的式子,并分析最值.
