河北省石家庄市晋州市2023-2024学年八年级上学期期中数学试题(无答案)
文档属性
| 名称 | 河北省石家庄市晋州市2023-2024学年八年级上学期期中数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 769.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 00:00:00 | ||
图片预览


文档简介
晋州市2023-2024学年度第一学期期中考试八年级
数学试卷
题号 一 二 三 总分
得分 20 21 22 23 24 25 26
一、选择题(本大题共16个小题,共38分. 1~6小题各3分;7~16小题各2分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案
1. 下列各数中为无理数的是
A. B. 1. 234 C. 0 D.
2. 实数的相反数是
A. B. 3 C. D.
3. 估计的值在
A. 2和3之间 B. 3和4之间 C. 4和5之间 D. 5和6之间
4. 如图所示,,则的度数为
A. B. C. D.
5. 如图所示,与相交于点,不添加辅助线,就可以判定,判定全等的依据是
A. SSS B. SAS C. AAS D. 以上均可以
6. 要使分式有意义,则应满足
A. B. C. D.
7. 下列命题中,是假命题的为
A. (把自然数按顾序依次无限写下去)是无理数
B. 0没有算术平方根
C. 对顶角相等
D. 如果直线,那么直线
8. 如图所示,嘉淇家装饰窗格中的一块三角形形状的玻璃坏了,需要重新配一块. 嘉淇通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是
A. B.
C. D.
9. 若是自然数,则表示的值的对应点落在数轴(如图)上的范围是
A. ① B. ② C. ③ D. ①②③均有可能
10. 嘉淇解分式方程的过程如下:
解:去分母,得 ①
去括号,得 ②
移项、合并同类项,得 ③
因为时,各分母均不为0,
所以,原分式方程的解是. ④
以上步骤中,最开始出错的一步是
A. ① B. ② C. ③ D. ④
11. 若在解关于的方程时,会产生增根,则的值为
A. 3 B. C. 1 D.
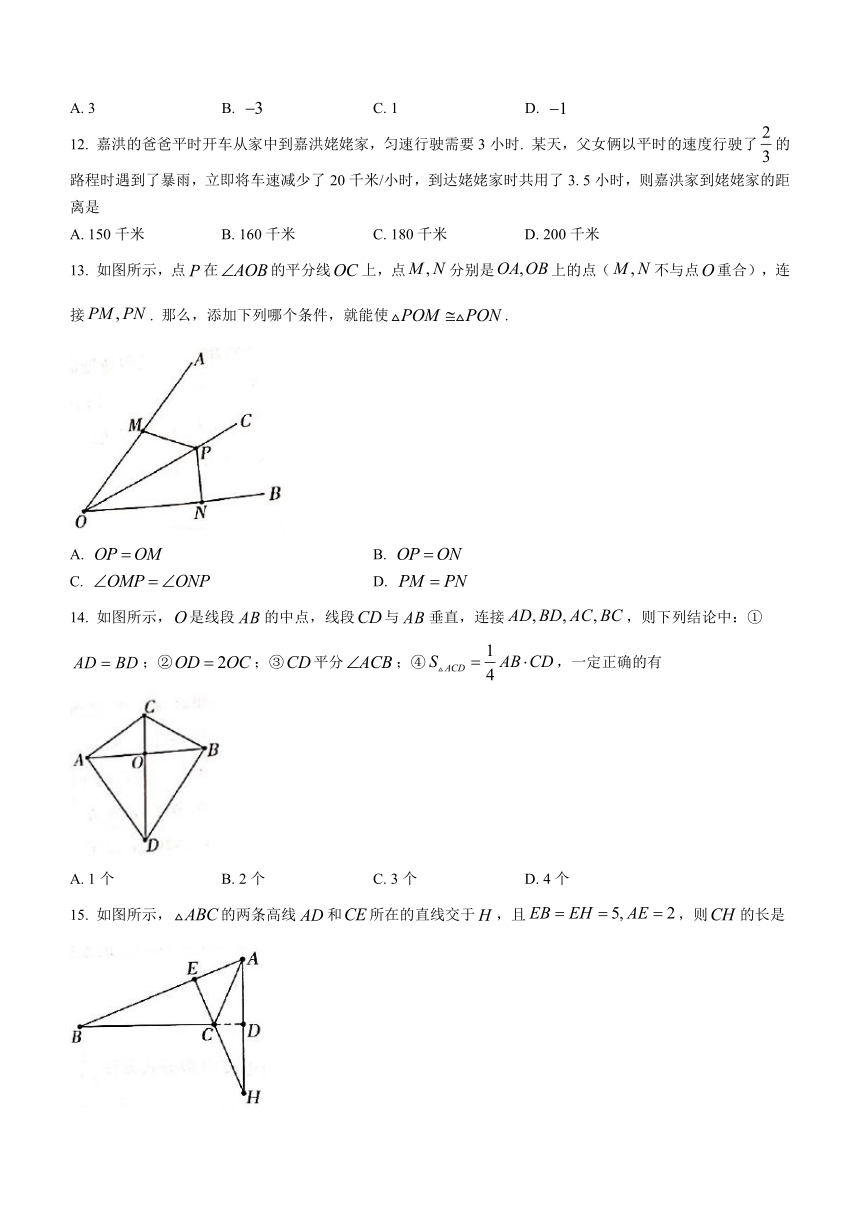
12. 嘉洪的爸爸平时开车从家中到嘉洪姥姥家,匀速行驶需要3小时. 某天,父女俩以平时的速度行驶了的路程时遇到了暴雨,立即将车速减少了20千米/小时,到达姥姥家时共用了3. 5小时,则嘉洪家到姥姥家的距离是
A. 150千米 B. 160千米 C. 180千米 D. 200千米
13. 如图所示,点在的平分线上,点分别是上的点(不与点重合),连接. 那么,添加下列哪个条件,就能使.
A. B.
C. D.
14. 如图所示,是线段的中点,线段与垂直,连接,则下列结论中:①;②;③平分;④,一定正确的有
A. 1个 B. 2个 C. 3个 D. 4个
15. 如图所示,的两条高线和所在的直线交于,且,则的长是
A. 2 B. 3 C. 3. 5 D. 4
16. 用尺规作的平分线,嘉嘉和淇淇采用了不同的方法:
①嘉嘉:如图(1),以为圆心,适当长为半径画弧,分别交于点;再分别以,为圆心,大于的长为半径,在内部画弧,两弧相交于点,则射线即为的平分线.
②淇淇:如图(2),以为圆心,两个不同的适当长度为半径画弧,分别交于点,和;连接,两线相交于点,则射线即为的平分线.
对于两人的作法,下列判断正确的是
图(1) 图(2)
A. 嘉嘉正确,淇淇错误 B. 嘉嘉错误,淇淇正确
C. 两人均错误 D. 两人均正确
二、填空题(本大题共3个小题,共10分. 17小题2分,18~19小题各4分,每空2分. 请把答案写在题目中的横线上)
17. 实数13的算术平方根为___________.
18. 若,则___________,___________.
19. 如图所示,平分的延长线交于点,连接,若,请解决下列问题:
①设,则___________(填“=”“>”“<”“≥”或“≤”);
②的面积是面积的___________倍.
三、解答题(本大题共7个小题,共72分. 解答应写出文字说明、证明过程或演算步骤)
20. (本题共2个小题,共9分. 其中,第一小题5分,第二小题4分)
(1)求的值:
(2)计算:
21. (本小题满分9分)
先化简,再求值:,其中,是最大的负整数.
22. (本小题满分9分)
解方程:.
23. (本小题满分10分)
如图,已知平分,在的反向延长上取一点,连接.
(1)求证:;
(2)若,求的大小.
24. (本小题满分10分)
在国庆节期间,学校举行了诗歌朗诵等系列活动,嘉嘉和淇淇负责为班级参赛学生购置纪念品. 他们发现,一个笔记本比一支钢笔贵3元,用225元购买的笔记本数量与用180元购买的钢笔数量相同.
(1)笔记本和钢笔的单价各多少元?
(2)若给参赛的30名学生每人发放一个笔记本或一支钢笔作为活动纪念品,要使购买纪念品的总费用不超过380元,最多可以购买多少个笔记本?
25. (本小题满分12分)
认真观察下列五行数,解决后面的问题.
第1行 1 2 3 4 5 6 7
第2行 4 16 36
第3行 1 13 33
第4行 1
第5行
【观察发现】对比第行的数的发展规律,可以发现:
(1)第行的第10个数分别是___________、___________、___________;
(2)设第2行的第(为正整数)个数为,则与的关系式可表示为___________(填写序号即可).
①;②;③;④.
(3)设第2,4行的第个数分别为,则___________(用含的式子表示).
【类比探索】设第2,5行的第个数分别为,类比第行的数发展规律的探索过程,对比第行的数的发展规律,可以发现:___________(用含的式子表示).
【解决问题】是否存在一个值,使?若存在,求出及对应的值;若不存在,请说明理由.
26. (本小题满分13分)
【模型呈现】如图(1)和(2)所示,,直线经过点(不与重合),过点作的垂线,垂足分别为,则有.
图(1) 图(2)
(1)请你针对图(1)给出证明.
【模型应用】在图(1)的基础上,在射线上取一点,把线段绕点逆时针转得到,连接,交直线于点.
图(3) 图(4) 图(5)
(2)如图(3),当点与点重合时,与的数量关系为___________;
(3)如图(4),当点在的延长线上时,请判断与的数量关系,并给出证明;
(4)如图(5),当点在线段上时,的值为___________.
数学试卷
题号 一 二 三 总分
得分 20 21 22 23 24 25 26
一、选择题(本大题共16个小题,共38分. 1~6小题各3分;7~16小题各2分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案
1. 下列各数中为无理数的是
A. B. 1. 234 C. 0 D.
2. 实数的相反数是
A. B. 3 C. D.
3. 估计的值在
A. 2和3之间 B. 3和4之间 C. 4和5之间 D. 5和6之间
4. 如图所示,,则的度数为
A. B. C. D.
5. 如图所示,与相交于点,不添加辅助线,就可以判定,判定全等的依据是
A. SSS B. SAS C. AAS D. 以上均可以
6. 要使分式有意义,则应满足
A. B. C. D.
7. 下列命题中,是假命题的为
A. (把自然数按顾序依次无限写下去)是无理数
B. 0没有算术平方根
C. 对顶角相等
D. 如果直线,那么直线
8. 如图所示,嘉淇家装饰窗格中的一块三角形形状的玻璃坏了,需要重新配一块. 嘉淇通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是
A. B.
C. D.
9. 若是自然数,则表示的值的对应点落在数轴(如图)上的范围是
A. ① B. ② C. ③ D. ①②③均有可能
10. 嘉淇解分式方程的过程如下:
解:去分母,得 ①
去括号,得 ②
移项、合并同类项,得 ③
因为时,各分母均不为0,
所以,原分式方程的解是. ④
以上步骤中,最开始出错的一步是
A. ① B. ② C. ③ D. ④
11. 若在解关于的方程时,会产生增根,则的值为
A. 3 B. C. 1 D.
12. 嘉洪的爸爸平时开车从家中到嘉洪姥姥家,匀速行驶需要3小时. 某天,父女俩以平时的速度行驶了的路程时遇到了暴雨,立即将车速减少了20千米/小时,到达姥姥家时共用了3. 5小时,则嘉洪家到姥姥家的距离是
A. 150千米 B. 160千米 C. 180千米 D. 200千米
13. 如图所示,点在的平分线上,点分别是上的点(不与点重合),连接. 那么,添加下列哪个条件,就能使.
A. B.
C. D.
14. 如图所示,是线段的中点,线段与垂直,连接,则下列结论中:①;②;③平分;④,一定正确的有
A. 1个 B. 2个 C. 3个 D. 4个
15. 如图所示,的两条高线和所在的直线交于,且,则的长是
A. 2 B. 3 C. 3. 5 D. 4
16. 用尺规作的平分线,嘉嘉和淇淇采用了不同的方法:
①嘉嘉:如图(1),以为圆心,适当长为半径画弧,分别交于点;再分别以,为圆心,大于的长为半径,在内部画弧,两弧相交于点,则射线即为的平分线.
②淇淇:如图(2),以为圆心,两个不同的适当长度为半径画弧,分别交于点,和;连接,两线相交于点,则射线即为的平分线.
对于两人的作法,下列判断正确的是
图(1) 图(2)
A. 嘉嘉正确,淇淇错误 B. 嘉嘉错误,淇淇正确
C. 两人均错误 D. 两人均正确
二、填空题(本大题共3个小题,共10分. 17小题2分,18~19小题各4分,每空2分. 请把答案写在题目中的横线上)
17. 实数13的算术平方根为___________.
18. 若,则___________,___________.
19. 如图所示,平分的延长线交于点,连接,若,请解决下列问题:
①设,则___________(填“=”“>”“<”“≥”或“≤”);
②的面积是面积的___________倍.
三、解答题(本大题共7个小题,共72分. 解答应写出文字说明、证明过程或演算步骤)
20. (本题共2个小题,共9分. 其中,第一小题5分,第二小题4分)
(1)求的值:
(2)计算:
21. (本小题满分9分)
先化简,再求值:,其中,是最大的负整数.
22. (本小题满分9分)
解方程:.
23. (本小题满分10分)
如图,已知平分,在的反向延长上取一点,连接.
(1)求证:;
(2)若,求的大小.
24. (本小题满分10分)
在国庆节期间,学校举行了诗歌朗诵等系列活动,嘉嘉和淇淇负责为班级参赛学生购置纪念品. 他们发现,一个笔记本比一支钢笔贵3元,用225元购买的笔记本数量与用180元购买的钢笔数量相同.
(1)笔记本和钢笔的单价各多少元?
(2)若给参赛的30名学生每人发放一个笔记本或一支钢笔作为活动纪念品,要使购买纪念品的总费用不超过380元,最多可以购买多少个笔记本?
25. (本小题满分12分)
认真观察下列五行数,解决后面的问题.
第1行 1 2 3 4 5 6 7
第2行 4 16 36
第3行 1 13 33
第4行 1
第5行
【观察发现】对比第行的数的发展规律,可以发现:
(1)第行的第10个数分别是___________、___________、___________;
(2)设第2行的第(为正整数)个数为,则与的关系式可表示为___________(填写序号即可).
①;②;③;④.
(3)设第2,4行的第个数分别为,则___________(用含的式子表示).
【类比探索】设第2,5行的第个数分别为,类比第行的数发展规律的探索过程,对比第行的数的发展规律,可以发现:___________(用含的式子表示).
【解决问题】是否存在一个值,使?若存在,求出及对应的值;若不存在,请说明理由.
26. (本小题满分13分)
【模型呈现】如图(1)和(2)所示,,直线经过点(不与重合),过点作的垂线,垂足分别为,则有.
图(1) 图(2)
(1)请你针对图(1)给出证明.
【模型应用】在图(1)的基础上,在射线上取一点,把线段绕点逆时针转得到,连接,交直线于点.
图(3) 图(4) 图(5)
(2)如图(3),当点与点重合时,与的数量关系为___________;
(3)如图(4),当点在的延长线上时,请判断与的数量关系,并给出证明;
(4)如图(5),当点在线段上时,的值为___________.
同课章节目录
