第五章 圆培优专题 垂径定理的应用(含答案)
文档属性
| 名称 | 第五章 圆培优专题 垂径定理的应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 21:00:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
培优专题:垂径定理的应用
应用一:与三角函数整合
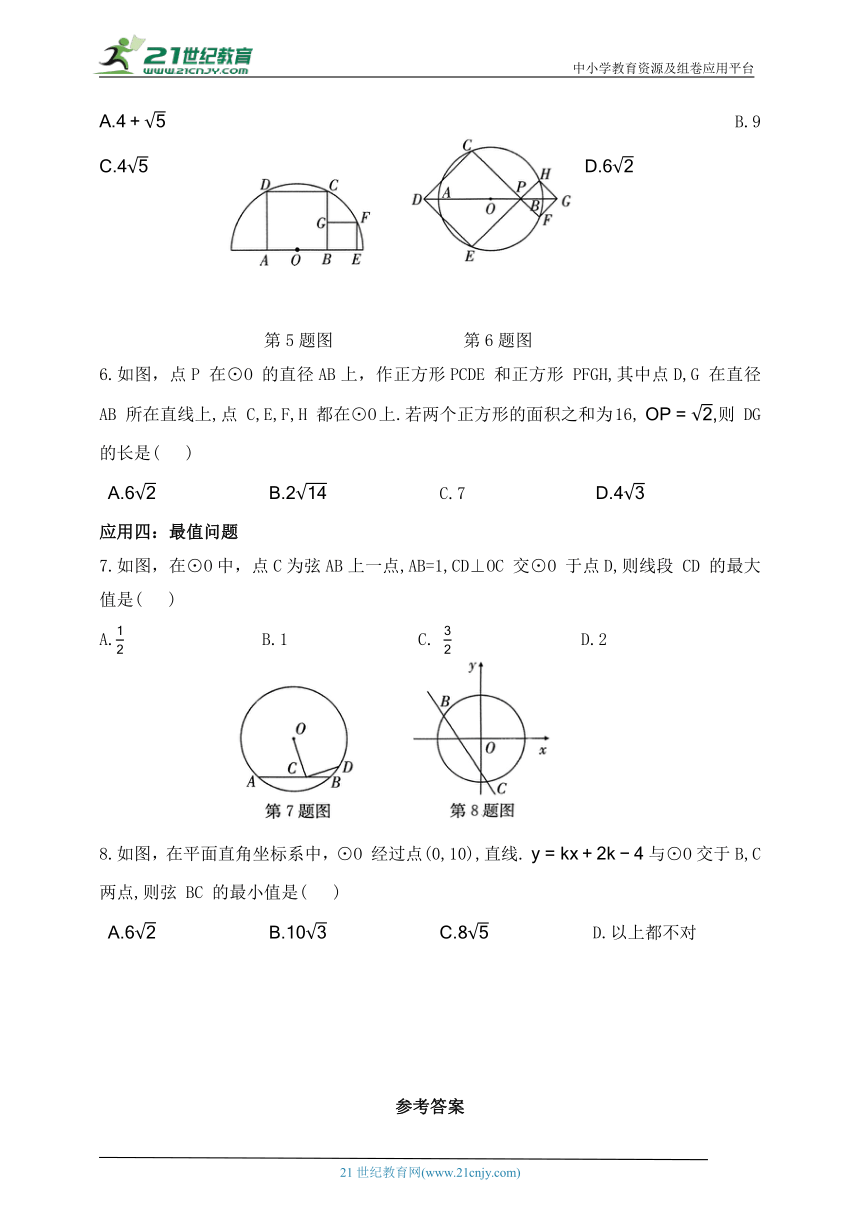
1.如图,⊙O的半径为9,弦AB⊥半径OC 于点则 AB 的长度为( )
A.6 B.12 C.9
第1题图 第2题图
2.如图,在半径为 4.5 的⊙O 内有两条互相垂直的弦AB 和CD, 6,垂足为 E,则 的值是( )
应用二:与坐标系(函数)整合
3.如图,在平面直角坐标系中,⊙A 的圆心在x轴上,且半径AO 的端点与原点O 重合,平行于 x 轴的直线交⊙A 于 M,N 两点,如果点M的坐标是 那么点 N 的 坐标为_____________.
第3题图 第4题图
4.如图,在平面直角坐标系中,⊙P的圆心是(3,a) 半径为 3,函数 的图象被⊙P截得的弦AB的长为则 a 的值是____________.
应用三:与正方形、一元二次方程整合
5.如图,正方形ABCD 和正方形BEFG 的顶点分别在半圆O 的直径和圆周上,若. 则半圆O 的半径是( )
B.9
第5题图 第6题图
6.如图,点P 在⊙O 的直径AB上,作正方形PCDE 和正方形 PFGH,其中点D,G 在直径AB 所在直线上,点 C,E,F,H 都在⊙O上.若两个正方形的面积之和为16, 则 DG 的长是( )
C.7
应用四:最值问题
7.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC 交⊙O 于点D,则线段 CD 的最大值是( )
A. B.1 C. D.2
8.如图,在平面直角坐标系中,⊙O 经过点(0,10),直线. 与⊙O交于B,C 两点,则弦 BC 的最小值是( )
D.以上都不对
参考答案
1. B
2. D [解析]如图,作OM⊥AB 于点M,ON⊥CD 于点N,连接OB,OD.由垂径定理得 DN由勾股定理得 同 理,得 ∵弦 AB,CD 互相垂直,OM⊥AB,ON⊥CD,∴∠MEN=∠OME=∠ONE=90°,∴四边形MONE 是矩形,
3.(-1,-2) [解析]如图,分别过点M,N作x轴的垂线,过点 A作AB⊥MN,连接 AN,则 BM=BN.设⊙A的半径为r,则AN=r,BM=BN=4-r.在Rt△ABN 中,根据勾股定理得 解得 r=2.5,∴BN=4-2.5=1.5,则点 N 到y轴的距离为AO-BN=2.5-1.5=1.又∵点N 在第三象限,∴点N 的坐标为(-1,-2).
[解析]如图,过点 P 作PC⊥x轴于点C,交 AB于点D,作 PE⊥AB于点E,连接 PB.∵⊙P 的圆心坐标是(3,a),∴OC=3,PC=a.把x=3代入y=x得y=3,∴D点坐标为(3,3),∴CD=3,∴△OCD为等腰直角三角形,∴△PED也为等腰直角三角形.∵PE⊥AB,∴AE=在 Rt△PBE 中,PB=3,∴PE=1,∴PD= PE= ,∴a=3+ .
5. C [解析]如图,连接OC,OF,设 OB=x.∵四边形ABCD是正方形且顶点 D和C 在圆周上,∴AB=BC=2x,∠OBC=90°.∵BG=4,四边形 BEFG 是正方形,∴OE=x+4,EF = BE= BG =4, ∠FEB = 90°.在Rt△BCO中, 在 Rt△FEO中, 解得 x=4或x=-2(舍去).当x=4时,OC=4 ,则半圆O的半径是
6. B [解析]如图,作OK⊥PC 于点K,设正方形 PFGH 的边长是x.∵四边形 PCDE 是正方形,∴∠CPD=45°.∵∠OKP=90°,∴△KOP 是等腰直角三角形,∴PK=
∵两个正方形的面积之和为
或 (舍),∴PC=x+2= +1,PH
7. A [解析]如图,连接OD.∵CD⊥OC 交⊙O 于点D,∴△OCD 是 直 角 三 角 形. 根 据 勾 股 定 理 得 CD=半径 OD 是定值,当OC⊥AB 时,线段OC最小,此时 D 与 B 重合, 即线段 CD 的最大值是
8. C [解析]对于直线y=kx+2k-4,当x=-2时,y=-4,故直线y=kx+2k-4恒经过点(-2,-4),记为点D.连接OB,OD,如图.由于过圆内定点 D 的所有弦中,与OD 垂直的弦最短,即当DB⊥OD时,BC 最短.∵D(-2,⊙O经过点(0,
=4 .
∵DB⊥OD,∴BC=2BD=8 ,∴弦 BC 的最小值是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
培优专题:垂径定理的应用
应用一:与三角函数整合
1.如图,⊙O的半径为9,弦AB⊥半径OC 于点则 AB 的长度为( )
A.6 B.12 C.9
第1题图 第2题图
2.如图,在半径为 4.5 的⊙O 内有两条互相垂直的弦AB 和CD, 6,垂足为 E,则 的值是( )
应用二:与坐标系(函数)整合
3.如图,在平面直角坐标系中,⊙A 的圆心在x轴上,且半径AO 的端点与原点O 重合,平行于 x 轴的直线交⊙A 于 M,N 两点,如果点M的坐标是 那么点 N 的 坐标为_____________.
第3题图 第4题图
4.如图,在平面直角坐标系中,⊙P的圆心是(3,a) 半径为 3,函数 的图象被⊙P截得的弦AB的长为则 a 的值是____________.
应用三:与正方形、一元二次方程整合
5.如图,正方形ABCD 和正方形BEFG 的顶点分别在半圆O 的直径和圆周上,若. 则半圆O 的半径是( )
B.9
第5题图 第6题图
6.如图,点P 在⊙O 的直径AB上,作正方形PCDE 和正方形 PFGH,其中点D,G 在直径AB 所在直线上,点 C,E,F,H 都在⊙O上.若两个正方形的面积之和为16, 则 DG 的长是( )
C.7
应用四:最值问题
7.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC 交⊙O 于点D,则线段 CD 的最大值是( )
A. B.1 C. D.2
8.如图,在平面直角坐标系中,⊙O 经过点(0,10),直线. 与⊙O交于B,C 两点,则弦 BC 的最小值是( )
D.以上都不对
参考答案
1. B
2. D [解析]如图,作OM⊥AB 于点M,ON⊥CD 于点N,连接OB,OD.由垂径定理得 DN由勾股定理得 同 理,得 ∵弦 AB,CD 互相垂直,OM⊥AB,ON⊥CD,∴∠MEN=∠OME=∠ONE=90°,∴四边形MONE 是矩形,
3.(-1,-2) [解析]如图,分别过点M,N作x轴的垂线,过点 A作AB⊥MN,连接 AN,则 BM=BN.设⊙A的半径为r,则AN=r,BM=BN=4-r.在Rt△ABN 中,根据勾股定理得 解得 r=2.5,∴BN=4-2.5=1.5,则点 N 到y轴的距离为AO-BN=2.5-1.5=1.又∵点N 在第三象限,∴点N 的坐标为(-1,-2).
[解析]如图,过点 P 作PC⊥x轴于点C,交 AB于点D,作 PE⊥AB于点E,连接 PB.∵⊙P 的圆心坐标是(3,a),∴OC=3,PC=a.把x=3代入y=x得y=3,∴D点坐标为(3,3),∴CD=3,∴△OCD为等腰直角三角形,∴△PED也为等腰直角三角形.∵PE⊥AB,∴AE=在 Rt△PBE 中,PB=3,∴PE=1,∴PD= PE= ,∴a=3+ .
5. C [解析]如图,连接OC,OF,设 OB=x.∵四边形ABCD是正方形且顶点 D和C 在圆周上,∴AB=BC=2x,∠OBC=90°.∵BG=4,四边形 BEFG 是正方形,∴OE=x+4,EF = BE= BG =4, ∠FEB = 90°.在Rt△BCO中, 在 Rt△FEO中, 解得 x=4或x=-2(舍去).当x=4时,OC=4 ,则半圆O的半径是
6. B [解析]如图,作OK⊥PC 于点K,设正方形 PFGH 的边长是x.∵四边形 PCDE 是正方形,∴∠CPD=45°.∵∠OKP=90°,∴△KOP 是等腰直角三角形,∴PK=
∵两个正方形的面积之和为
或 (舍),∴PC=x+2= +1,PH
7. A [解析]如图,连接OD.∵CD⊥OC 交⊙O 于点D,∴△OCD 是 直 角 三 角 形. 根 据 勾 股 定 理 得 CD=半径 OD 是定值,当OC⊥AB 时,线段OC最小,此时 D 与 B 重合, 即线段 CD 的最大值是
8. C [解析]对于直线y=kx+2k-4,当x=-2时,y=-4,故直线y=kx+2k-4恒经过点(-2,-4),记为点D.连接OB,OD,如图.由于过圆内定点 D 的所有弦中,与OD 垂直的弦最短,即当DB⊥OD时,BC 最短.∵D(-2,⊙O经过点(0,
=4 .
∵DB⊥OD,∴BC=2BD=8 ,∴弦 BC 的最小值是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
