广西壮族自治区2020年7月普通高中学业水平考试数学试卷(含解析)
文档属性
| 名称 | 广西壮族自治区2020年7月普通高中学业水平考试数学试卷(含解析) | 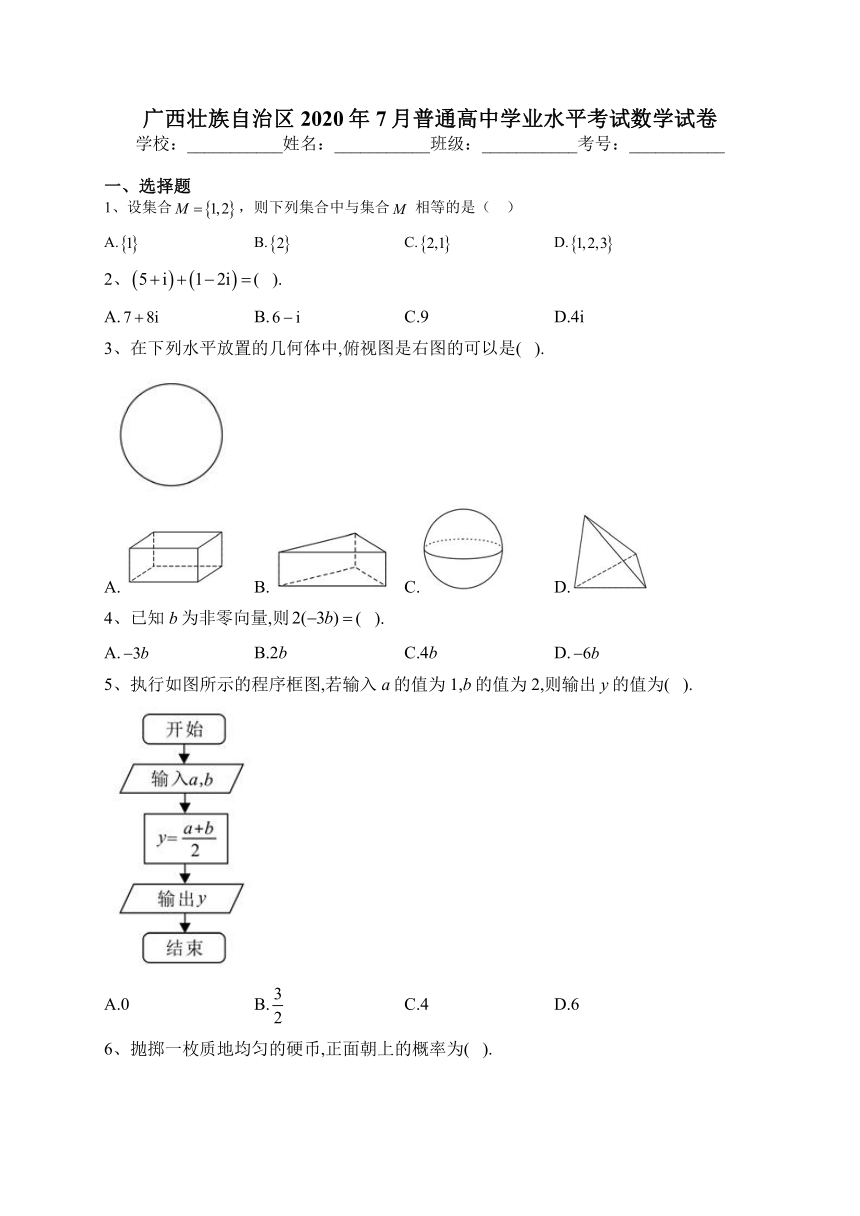 | |
| 格式 | docx | ||
| 文件大小 | 654.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 21:07:42 | ||
图片预览





文档简介
广西壮族自治区2020年7月普通高中学业水平考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、设集合,则下列集合中与集合相等的是( )
A. B. C. D.
2、( ).
A. B. C.9 D.4i
3、在下列水平放置的几何体中,俯视图是右图的可以是( ).
A. B. C. D.
4、已知b为非零向量,则( ).
A. B.2b C.4b D.
5、执行如图所示的程序框图,若输入a的值为1,b的值为2,则输出y的值为( ).
A.0 B. C.4 D.6
6、抛掷一枚质地均匀的硬币,正面朝上的概率为( ).
A. B. C. D.1
7、2015年以来,我国的年度GDP数据如下表:
时间(年) 2015 2016 2017 2018 2019
GDP(万亿元) 68.5506 74.4127 82.7121 91.9281 99.0865
设时间为n,与其对应的年度GDP为,那么( ).
A.68.5506 B.74.4127 C.82.7121 D.91.9281
8、下列命题是真命题的是( ).
A.3能被2整除 B.对顶角不相等 C.5是偶数 D.
9、时间经过3小时整,时针转过的弧度数为( ).
A. B. C. D.
10、指数函数的图象一定经过点( ).
A. B. C. D.
11、我国南北朝时期的数学家祖冲之的儿子祖晦提出了著名的体积计算原理:“幂势既同,则积不容异.”意思是说,如果两个等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.根据这个原理,可推出球的体积公式为,其中R是球的半径.已知球的半径等于3,那么它的体积等于( ).
A. B. C. D.
12、如图,在平面直角坐标系中,向量( ).
A. B. C. D.
13、在平面直角坐标系中,圆心在原点半径为3的圆的方程是( ).
A. B. C. D.
14、已知向量a与b的夹角为.满足,且,,则( ).
A. B. C. D.
15、已知为第一象限角,且,则( ).
A. B. C. D.
16、在平面直角坐标系中,双曲线的图象大致是( ).
A. B. C. D.
17、经过两点,的直线l的倾斜角等于( ).
A. B. C. D.
18、如图,把一张长方形的纸对折两次,然后打开,得到三条折痕a,b,c,下列结论正确的是( ).
A. B.,且a与c相交
C.且a与c相交 D.a,b,c两两相交
19、函数的最小值为( ).
A.1 B.5 C.8 D.10
20、已知,则的最小值为( ).
A.1 B. C. D.
21、某品牌电视专卖店在国庆七天长假的日销售量(单位:台)的茎叶图如图所示,则其国庆期间的日平均销售量是( ).
A.18台 B.16台 C.14台 D.12台
22、若实数满足,则的最大值为( ).
A.0 B.1 C.2 D.3
23、函数,的最小正周期是( ).
A. B. C. D.
24、设直线与直线的交点为P,则点P的坐标为( ).
A. B. C. D.
25、不等式的解集为( ).
A. B. C. D.
26、的值是( ).
A. B. C. D.2
27、如图,在长方体中,下列关系正确的是( ).
A.在平面ABCD内 B.平面ABCD
C.平面ABCD D.平面
28、函数的零点的个数为( ).
A.3 B.2 C.1 D.0
29、在中,角A,B,C的对边分别为a,b,c,若,,,则( ).
A.1 B.2 C.3 D.4
30、已知数列的前4项依次为1,3,6,10,那么它的一个通项公式是( ).
A. B. C. D.
二、填空题
31、________.
32、下列图案由正六边形拼成,按此规律,第四个图案的线段总数为________.
33、函数的定义域为________.
34、已知,是椭圆的两个焦点,点在椭圆上,轴,则的面积为________
三、解答题
35、作为重要的文化传播媒介,电影不仅可以拓宽青少年的视野,还能提高其艺术鉴赏能力.进电影院看电影是当下许多年轻人喜爱的休闲娱乐方式.某电影院IMAX巨幕放映厅第一排有8个座位,从第二排起,每一排都比它的前一排多1个座位,共有10排.试问该放映厅一共有多少个座位
36、某学校高二年级学生共400人,将其体育达标测试成绩(单位:分)按区间,,,,分组,由此绘制的频率分布直方图如图所示.规定成绩不低于80分为优秀.
(1)求成绩优秀的学生人数;
(2)从成绩优秀的学生中按组分层抽样选出5人,再从这5人中选出2人,求这2人的成绩都在区间的概率.
37、如图,四棱锥的底面ABCD为矩形,底面ABCD,,点E是棱PB的中点.
(1)求证:;
(2)若,,求三棱锥的体积.
(参考公式:锥体体积公式,其中S为底面面积,h为高.)
38、已知
(1)当时,求的单调区间;
(2)讨论函数的零点的个数情况.
参考答案
1、答案:C
解析:集合 ,
集合中与集合 相等的集合中有且只有元素 1,2 ,
与集合 相等的是.
故选 C:.
2、答案:B
解析:,
故选B.
3、答案:C
解析:结合选项分析出,只有C选项中球的俯视图是圆,故选:C.
4、答案:D
解析:.
故选:D.
5、答案:B
解析:由程序框图可知输入,,输出.
故选:B
6、答案:A
解析:
7、答案:D
解析:由题意可得,
故选:D.
8、答案:D
解析:3不能被2整除,故A错误;
对顶角相等,故B错误;
5是奇数,故C错误;
,故D正确
故选:D
9、答案:A
解析:时间经过四小时,时针转了,
故选:A.
10、答案:A
解析:当时,,所以指数函数的图象一定经过点,故A正确;
当时,,所以指数函数的图象不经过点,故错误;
当时,,所以指数函数的图象不经过点,故C错误;
当时,,所以指数函数的图象不经过点,故D错误;
故选:A.
11、答案:C
解析:,
故选:C
12、答案:C
解析:
13、答案:C
解析:圆心在原点半径为3的圆的方程,
,
故选:C.
14、答案:A
解析:由题意知,.
故选:A.
15、答案:D
解析:
16、答案:D
解析:A图是椭圆,B图是圆,C图是直线,D图是双曲线.
故选:D.
17、答案:C
解析:直线l的斜率,所以倾斜角等于.
故选:C.
18、答案:A
解析:因为长方形的对边都是互相平行的,连续左右对折两次后,长方形上得到三条折痕a,b,c,这三条折痕中每两条折痕又互相平行,所以三条折痕互相平行,故选:A.
19、答案:A
解析:因为幂函数在R上单调递增,
所以在上单调递增,因此,
故选:A.
20、答案:B
解析:.
故选:B.
21、答案:D
解析:
22、答案:D
解析:作出实数x,y;满足的可行域,如图阴影部分所示,平移直线,
经过点时,z有最大值,即.
故正确答案为D.
23、答案:B
解析:
24、答案:B
解析:
25、答案:A
解析:函数,.
最小正周期是.
故选:B.
26、答案:C
解析:
故选:C.
27、答案:B
解析:B项,在长方体中,
平面平面,平面,故B项正确,A,C两项错误;D项,
平面,
与平面不平行D项错误,故选B,
28、答案:C
解析:令,得,所以函数的零点个数只有一个.
故选:C.
29、答案:B
解析:如图,
过C作交AB于点D
,
是等腰直角三角形,
,
在中,由勾股定理得,
,
,
,是直角三角形,
,
,
故选B.
30、答案:A
解析:
31、答案:2
解析:
32、答案:21
解析:第一个六边形的线段总数为6,第二个图案的线段总数为,
第三个图案的线段总数为,那么按照此规律,第四个图案的线段总数为.
故答案为:21
33、答案:
解析:
34、答案:
解析:
35、答案:125
解析:方法一:用表示第n排的座位数,易知是等差数列,其中,公差.
.
该放映厅的座位数即为数列的前10项和,
所以该放映厅一共有125个座位.
方法二:用表示第n排的座位数,易知是等差数列,其中,公差.
由等差数列的前n项和,
得等差数列的前10项和
所以该放映厅一共有125个座位.
方法三:依题意,从第1排到第10排的座位数依次为8,9,10,..,18.第1排到第10排的座位数之和
所以该放映厅一共有125个座位.
36、答案:(1)100
(2)0.1
解析:(1)由频率分布直方图知,
成绩在区间内的学生有(人),
成绩在区间内的学生有(人).
(人),所以成绩优秀的学生有100人.
(2)用分层抽样的方法从优秀的学生中任选5人,
即从成绩在区间内的学生中抽取(人),
记此3人分别为A,B,C;
从成绩在区间内的学生中抽取(人),
记此2人分别为M,N.
从这5人中任选2人的选法有,,,,,,,,,,共10种,其中2人的成绩都在区间内的选法有,共1种.
故所选2人的成绩都在区间内的概率.
37、答案:(1)见解析
(2)
解析:(1)证明:底面ABCD,平面ABCD,
.
底面ABCD为矩形,
.
又,平面PAB,平面PAB,平面PAB,
平面PAB.
平面PAB,
.
(2)在中,,
.
又E是棱PB的中点,
.
由(1)知,平面PAB,
是三棱锥的高.
,
.
38、答案:(1)见解析
(2)见解析
解析:(1)的定义域为.
当时,,.
当时,,,单调递增;
当时,,单调递减.
在上单调递减,在上单调递增.
(2),且.
①若,则,在上单调递减,
函数只有一个零点;
②若,当,即时,单调递增;
当,即时,单调递减.
当时,取到最小值.
(i)当时,
,
函数只有一个零点;
(ii)当时,,.
令,则.
在上单调递减..
.
存在,使得.
函数有两个零点1,;
(iii)当时,,.
令,,在上单调递增.
,,.
又,
存在,使得.
函数有两个零点1,.
综上所述,当时,函数有两个零点;
当时,函数只有一个零点.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、设集合,则下列集合中与集合相等的是( )
A. B. C. D.
2、( ).
A. B. C.9 D.4i
3、在下列水平放置的几何体中,俯视图是右图的可以是( ).
A. B. C. D.
4、已知b为非零向量,则( ).
A. B.2b C.4b D.
5、执行如图所示的程序框图,若输入a的值为1,b的值为2,则输出y的值为( ).
A.0 B. C.4 D.6
6、抛掷一枚质地均匀的硬币,正面朝上的概率为( ).
A. B. C. D.1
7、2015年以来,我国的年度GDP数据如下表:
时间(年) 2015 2016 2017 2018 2019
GDP(万亿元) 68.5506 74.4127 82.7121 91.9281 99.0865
设时间为n,与其对应的年度GDP为,那么( ).
A.68.5506 B.74.4127 C.82.7121 D.91.9281
8、下列命题是真命题的是( ).
A.3能被2整除 B.对顶角不相等 C.5是偶数 D.
9、时间经过3小时整,时针转过的弧度数为( ).
A. B. C. D.
10、指数函数的图象一定经过点( ).
A. B. C. D.
11、我国南北朝时期的数学家祖冲之的儿子祖晦提出了著名的体积计算原理:“幂势既同,则积不容异.”意思是说,如果两个等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.根据这个原理,可推出球的体积公式为,其中R是球的半径.已知球的半径等于3,那么它的体积等于( ).
A. B. C. D.
12、如图,在平面直角坐标系中,向量( ).
A. B. C. D.
13、在平面直角坐标系中,圆心在原点半径为3的圆的方程是( ).
A. B. C. D.
14、已知向量a与b的夹角为.满足,且,,则( ).
A. B. C. D.
15、已知为第一象限角,且,则( ).
A. B. C. D.
16、在平面直角坐标系中,双曲线的图象大致是( ).
A. B. C. D.
17、经过两点,的直线l的倾斜角等于( ).
A. B. C. D.
18、如图,把一张长方形的纸对折两次,然后打开,得到三条折痕a,b,c,下列结论正确的是( ).
A. B.,且a与c相交
C.且a与c相交 D.a,b,c两两相交
19、函数的最小值为( ).
A.1 B.5 C.8 D.10
20、已知,则的最小值为( ).
A.1 B. C. D.
21、某品牌电视专卖店在国庆七天长假的日销售量(单位:台)的茎叶图如图所示,则其国庆期间的日平均销售量是( ).
A.18台 B.16台 C.14台 D.12台
22、若实数满足,则的最大值为( ).
A.0 B.1 C.2 D.3
23、函数,的最小正周期是( ).
A. B. C. D.
24、设直线与直线的交点为P,则点P的坐标为( ).
A. B. C. D.
25、不等式的解集为( ).
A. B. C. D.
26、的值是( ).
A. B. C. D.2
27、如图,在长方体中,下列关系正确的是( ).
A.在平面ABCD内 B.平面ABCD
C.平面ABCD D.平面
28、函数的零点的个数为( ).
A.3 B.2 C.1 D.0
29、在中,角A,B,C的对边分别为a,b,c,若,,,则( ).
A.1 B.2 C.3 D.4
30、已知数列的前4项依次为1,3,6,10,那么它的一个通项公式是( ).
A. B. C. D.
二、填空题
31、________.
32、下列图案由正六边形拼成,按此规律,第四个图案的线段总数为________.
33、函数的定义域为________.
34、已知,是椭圆的两个焦点,点在椭圆上,轴,则的面积为________
三、解答题
35、作为重要的文化传播媒介,电影不仅可以拓宽青少年的视野,还能提高其艺术鉴赏能力.进电影院看电影是当下许多年轻人喜爱的休闲娱乐方式.某电影院IMAX巨幕放映厅第一排有8个座位,从第二排起,每一排都比它的前一排多1个座位,共有10排.试问该放映厅一共有多少个座位
36、某学校高二年级学生共400人,将其体育达标测试成绩(单位:分)按区间,,,,分组,由此绘制的频率分布直方图如图所示.规定成绩不低于80分为优秀.
(1)求成绩优秀的学生人数;
(2)从成绩优秀的学生中按组分层抽样选出5人,再从这5人中选出2人,求这2人的成绩都在区间的概率.
37、如图,四棱锥的底面ABCD为矩形,底面ABCD,,点E是棱PB的中点.
(1)求证:;
(2)若,,求三棱锥的体积.
(参考公式:锥体体积公式,其中S为底面面积,h为高.)
38、已知
(1)当时,求的单调区间;
(2)讨论函数的零点的个数情况.
参考答案
1、答案:C
解析:集合 ,
集合中与集合 相等的集合中有且只有元素 1,2 ,
与集合 相等的是.
故选 C:.
2、答案:B
解析:,
故选B.
3、答案:C
解析:结合选项分析出,只有C选项中球的俯视图是圆,故选:C.
4、答案:D
解析:.
故选:D.
5、答案:B
解析:由程序框图可知输入,,输出.
故选:B
6、答案:A
解析:
7、答案:D
解析:由题意可得,
故选:D.
8、答案:D
解析:3不能被2整除,故A错误;
对顶角相等,故B错误;
5是奇数,故C错误;
,故D正确
故选:D
9、答案:A
解析:时间经过四小时,时针转了,
故选:A.
10、答案:A
解析:当时,,所以指数函数的图象一定经过点,故A正确;
当时,,所以指数函数的图象不经过点,故错误;
当时,,所以指数函数的图象不经过点,故C错误;
当时,,所以指数函数的图象不经过点,故D错误;
故选:A.
11、答案:C
解析:,
故选:C
12、答案:C
解析:
13、答案:C
解析:圆心在原点半径为3的圆的方程,
,
故选:C.
14、答案:A
解析:由题意知,.
故选:A.
15、答案:D
解析:
16、答案:D
解析:A图是椭圆,B图是圆,C图是直线,D图是双曲线.
故选:D.
17、答案:C
解析:直线l的斜率,所以倾斜角等于.
故选:C.
18、答案:A
解析:因为长方形的对边都是互相平行的,连续左右对折两次后,长方形上得到三条折痕a,b,c,这三条折痕中每两条折痕又互相平行,所以三条折痕互相平行,故选:A.
19、答案:A
解析:因为幂函数在R上单调递增,
所以在上单调递增,因此,
故选:A.
20、答案:B
解析:.
故选:B.
21、答案:D
解析:
22、答案:D
解析:作出实数x,y;满足的可行域,如图阴影部分所示,平移直线,
经过点时,z有最大值,即.
故正确答案为D.
23、答案:B
解析:
24、答案:B
解析:
25、答案:A
解析:函数,.
最小正周期是.
故选:B.
26、答案:C
解析:
故选:C.
27、答案:B
解析:B项,在长方体中,
平面平面,平面,故B项正确,A,C两项错误;D项,
平面,
与平面不平行D项错误,故选B,
28、答案:C
解析:令,得,所以函数的零点个数只有一个.
故选:C.
29、答案:B
解析:如图,
过C作交AB于点D
,
是等腰直角三角形,
,
在中,由勾股定理得,
,
,
,是直角三角形,
,
,
故选B.
30、答案:A
解析:
31、答案:2
解析:
32、答案:21
解析:第一个六边形的线段总数为6,第二个图案的线段总数为,
第三个图案的线段总数为,那么按照此规律,第四个图案的线段总数为.
故答案为:21
33、答案:
解析:
34、答案:
解析:
35、答案:125
解析:方法一:用表示第n排的座位数,易知是等差数列,其中,公差.
.
该放映厅的座位数即为数列的前10项和,
所以该放映厅一共有125个座位.
方法二:用表示第n排的座位数,易知是等差数列,其中,公差.
由等差数列的前n项和,
得等差数列的前10项和
所以该放映厅一共有125个座位.
方法三:依题意,从第1排到第10排的座位数依次为8,9,10,..,18.第1排到第10排的座位数之和
所以该放映厅一共有125个座位.
36、答案:(1)100
(2)0.1
解析:(1)由频率分布直方图知,
成绩在区间内的学生有(人),
成绩在区间内的学生有(人).
(人),所以成绩优秀的学生有100人.
(2)用分层抽样的方法从优秀的学生中任选5人,
即从成绩在区间内的学生中抽取(人),
记此3人分别为A,B,C;
从成绩在区间内的学生中抽取(人),
记此2人分别为M,N.
从这5人中任选2人的选法有,,,,,,,,,,共10种,其中2人的成绩都在区间内的选法有,共1种.
故所选2人的成绩都在区间内的概率.
37、答案:(1)见解析
(2)
解析:(1)证明:底面ABCD,平面ABCD,
.
底面ABCD为矩形,
.
又,平面PAB,平面PAB,平面PAB,
平面PAB.
平面PAB,
.
(2)在中,,
.
又E是棱PB的中点,
.
由(1)知,平面PAB,
是三棱锥的高.
,
.
38、答案:(1)见解析
(2)见解析
解析:(1)的定义域为.
当时,,.
当时,,,单调递增;
当时,,单调递减.
在上单调递减,在上单调递增.
(2),且.
①若,则,在上单调递减,
函数只有一个零点;
②若,当,即时,单调递增;
当,即时,单调递减.
当时,取到最小值.
(i)当时,
,
函数只有一个零点;
(ii)当时,,.
令,则.
在上单调递减..
.
存在,使得.
函数有两个零点1,;
(iii)当时,,.
令,,在上单调递增.
,,.
又,
存在,使得.
函数有两个零点1,.
综上所述,当时,函数有两个零点;
当时,函数只有一个零点.
同课章节目录
