(备课参考)(新)湘教版数学七年级下5.3《图形变换的简单应用》PPT课件(1份)
文档属性
| 名称 | (备课参考)(新)湘教版数学七年级下5.3《图形变换的简单应用》PPT课件(1份) |  | |
| 格式 | zip | ||
| 文件大小 | 434.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-08 10:51:45 | ||
图片预览






文档简介
(共21张PPT)
图案欣赏
在平面内,将一个图形沿某个方向移动一定的距离,
这样的图形运动称为平移
平移的概念:
平移的性质:
1、平移不改变图形的大小和形状。
2、对应点所连的线平行且相等。
3、对应线段平行且相等。
4、对应角相等。
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等。
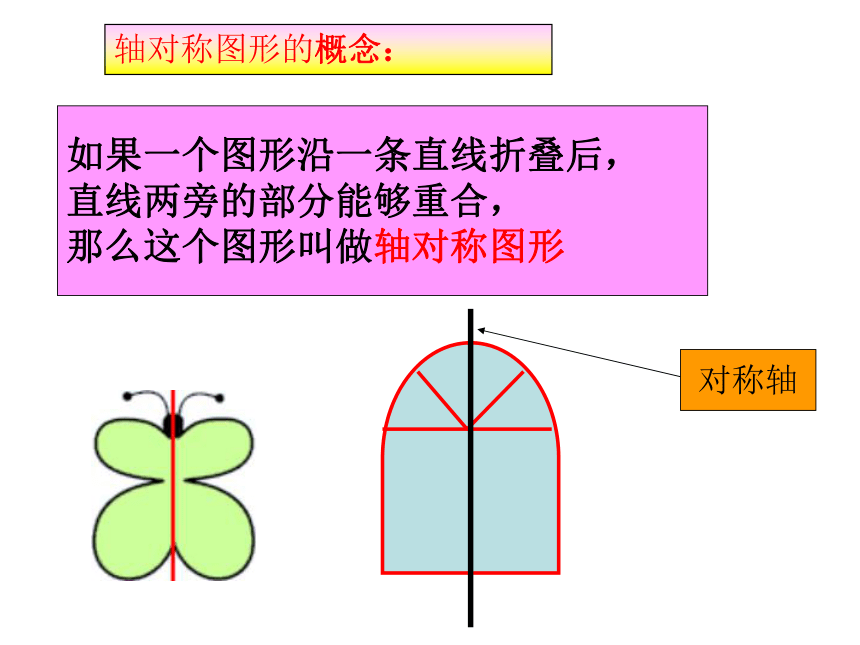
轴对称图形的概念:
如果一个图形沿一条直线折叠后,
直线两旁的部分能够重合,
那么这个图形叫做轴对称图形
对称轴
如图是由四部分组成的,每部分都包括两个“十”字,浅色部分能经过适当旋转的得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
(1) 旋转 可以看作是浅色部分通过三次旋转前后的图案共同组成的。(旋转中心是整个图形的中心,旋转角度分别是90度,180度,270度)
(2) 平移 也可以看做是由一个“十”字通过连续七次平移前后的图案共同组成的
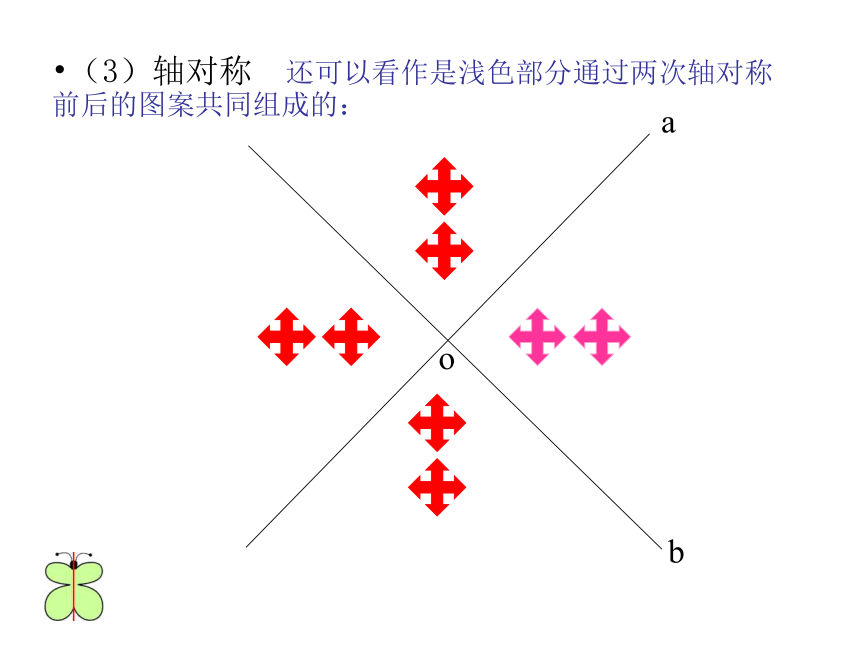
(3)轴对称 还可以看作是浅色部分通过两次轴对称前后的图案共同组成的:
a
b
o
(4)平移和旋转的组合 也可以看作是浅色部分先向左平移,再左右部分一起绕图形的中心旋转90度前后的图案共同组成的:
解:可以先将甲“树”绕图上的A点旋转,使得甲“树”被“扶直”,然后,再沿AB方向将所得“树”平移到B点位置,即可与乙“树”重合。
乙
A
B
甲
甲
例 1 如图,有甲、乙两棵“小树”,你能对甲“树”进行适当的操作,将它与乙“树”重合吗?写出你的操作过程。
方法一
解:先将甲“树” 沿AB方向平移到B点位置,再将甲“树”绕点B旋转“扶直”,即可与乙“树”重合。
乙
A
B
甲
甲
例 1 如图,有甲、乙两棵“小树”,你能对甲“树”进行适当的操作,将它与乙“树”重合吗?写出你的操作过程。
方法二
想一想
1、能将左图通过旋转或平移的到右图吗?
轴对称
a
1、如图,下列各组图案中怎样变化得到?
以左图案的中心为旋转中心,将图案按顺时针方向
旋转900,即可得到右边的图案。
练习
2、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,以三个正三角形的公共顶点为
旋转中心,分别按顺时针、逆时针方向旋转600,即可得到该图案。
练习
2、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,分别以这个三角形与相邻三角形
的公共边所在直线为对称轴作轴对称图形,也可得到该图案。
练习
2、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把左边的正三角形看做“基本图案”,以三个正三角形的公共顶点为
旋转中心,按顺时针方向旋转600,再把左边的正三角形向右平移与正三角形
边长相等的距离,即可得到该图案。
练习
观察图中的四个图案,它们可以分别看做是由什么“基本图案”
经过怎样的变化形成的?(不考虑颜色)
.
图案欣赏
图形间的变换关系
1 旋转——旋转中心、方向、角度和次数
2 平移——平移的方向、距离和次数
3 轴对称——对称轴
4 旋转与平移的组合
5 旋转与轴对称的组合
6 轴对称与平移的组合
找准基本图形
小结:
图案欣赏
在平面内,将一个图形沿某个方向移动一定的距离,
这样的图形运动称为平移
平移的概念:
平移的性质:
1、平移不改变图形的大小和形状。
2、对应点所连的线平行且相等。
3、对应线段平行且相等。
4、对应角相等。
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等。
轴对称图形的概念:
如果一个图形沿一条直线折叠后,
直线两旁的部分能够重合,
那么这个图形叫做轴对称图形
对称轴
如图是由四部分组成的,每部分都包括两个“十”字,浅色部分能经过适当旋转的得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
(1) 旋转 可以看作是浅色部分通过三次旋转前后的图案共同组成的。(旋转中心是整个图形的中心,旋转角度分别是90度,180度,270度)
(2) 平移 也可以看做是由一个“十”字通过连续七次平移前后的图案共同组成的
(3)轴对称 还可以看作是浅色部分通过两次轴对称前后的图案共同组成的:
a
b
o
(4)平移和旋转的组合 也可以看作是浅色部分先向左平移,再左右部分一起绕图形的中心旋转90度前后的图案共同组成的:
解:可以先将甲“树”绕图上的A点旋转,使得甲“树”被“扶直”,然后,再沿AB方向将所得“树”平移到B点位置,即可与乙“树”重合。
乙
A
B
甲
甲
例 1 如图,有甲、乙两棵“小树”,你能对甲“树”进行适当的操作,将它与乙“树”重合吗?写出你的操作过程。
方法一
解:先将甲“树” 沿AB方向平移到B点位置,再将甲“树”绕点B旋转“扶直”,即可与乙“树”重合。
乙
A
B
甲
甲
例 1 如图,有甲、乙两棵“小树”,你能对甲“树”进行适当的操作,将它与乙“树”重合吗?写出你的操作过程。
方法二
想一想
1、能将左图通过旋转或平移的到右图吗?
轴对称
a
1、如图,下列各组图案中怎样变化得到?
以左图案的中心为旋转中心,将图案按顺时针方向
旋转900,即可得到右边的图案。
练习
2、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,以三个正三角形的公共顶点为
旋转中心,分别按顺时针、逆时针方向旋转600,即可得到该图案。
练习
2、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,分别以这个三角形与相邻三角形
的公共边所在直线为对称轴作轴对称图形,也可得到该图案。
练习
2、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把左边的正三角形看做“基本图案”,以三个正三角形的公共顶点为
旋转中心,按顺时针方向旋转600,再把左边的正三角形向右平移与正三角形
边长相等的距离,即可得到该图案。
练习
观察图中的四个图案,它们可以分别看做是由什么“基本图案”
经过怎样的变化形成的?(不考虑颜色)
.
图案欣赏
图形间的变换关系
1 旋转——旋转中心、方向、角度和次数
2 平移——平移的方向、距离和次数
3 轴对称——对称轴
4 旋转与平移的组合
5 旋转与轴对称的组合
6 轴对称与平移的组合
找准基本图形
小结:
