5.2 二次函数的图像和性质(第2课时)课件(共31张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 5.2 二次函数的图像和性质(第2课时)课件(共31张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 00:00:00 | ||
图片预览






文档简介
第5章 二次函数
5.2 二次函数的图像和性质(2)
第2课时 二次函数y=ax2性质
学习目标
1.能归纳总结y=ax?(a≠0)的图像性质;
2.体会数形结合的思想方法.
观察与思考
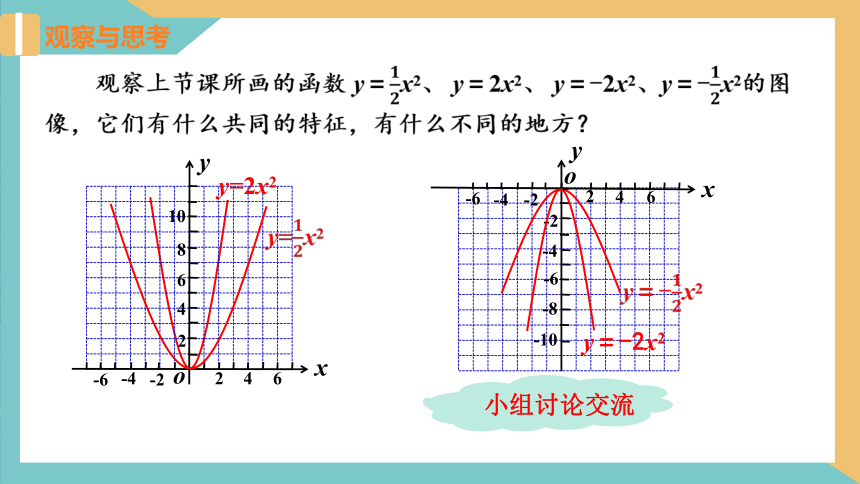
观察上节课所画的函数 y=????????x2、 y=2x2、 y=-2x2、y=-????????x2的图像,它们有什么共同的特征,有什么不同的地方?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
小组讨论交流
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
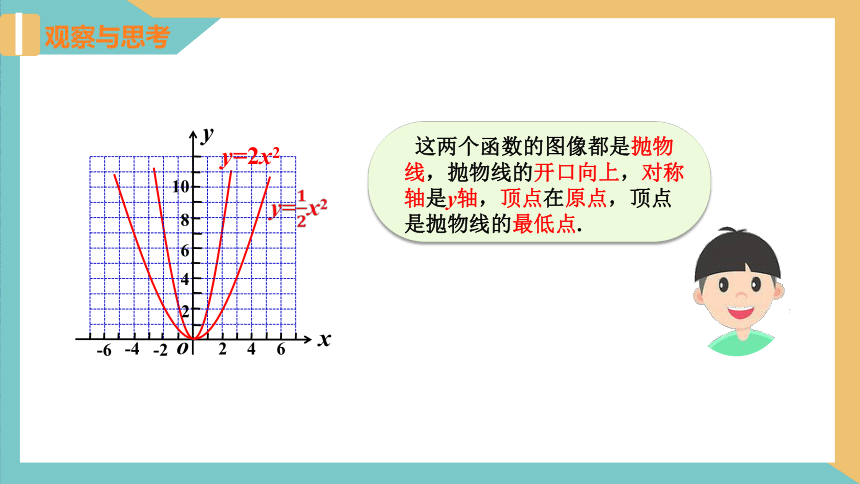
这两个函数的图像都是抛物线,抛物线的开口向上,对称轴是y轴,顶点在原点,顶点是抛物线的最低点.
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
这两个函数的图像都是抛物线,抛物线的开口向下,对称轴是y轴,顶点在原点,顶点是抛物线的最高点.
归纳总结
二次函数y=ax2的图像的性质1:
(1)二次函数y=ax?的图像是一条抛物线,抛物线的顶点在原点,对称轴为y轴.
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最低点.
(3)当a<0时,抛物线的开口向下,顶点是抛物线的最高点.
思考与探索
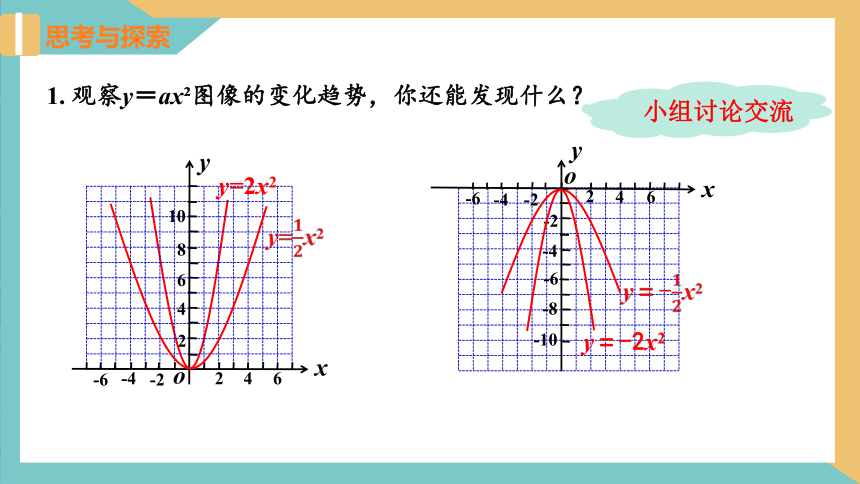
1. 观察y=ax?图像的变化趋势,你还能发现什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
小组讨论交流
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
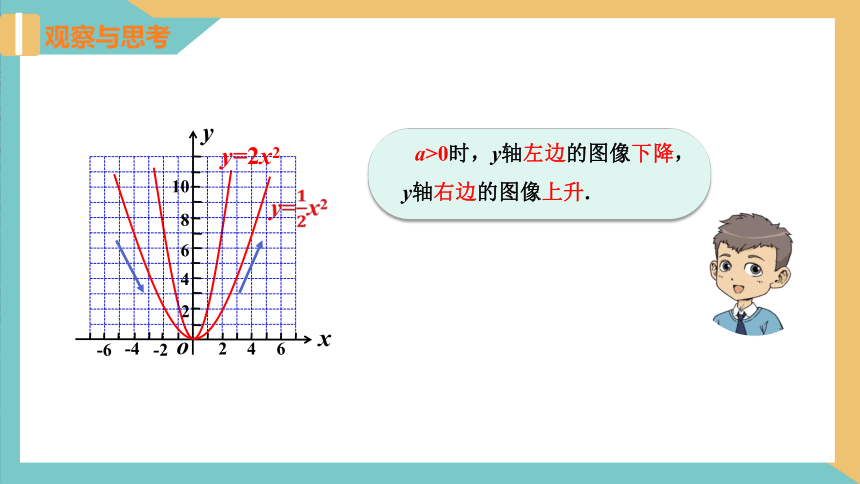
a>0时,y轴左边的图像下降,
y轴右边的图像上升.
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
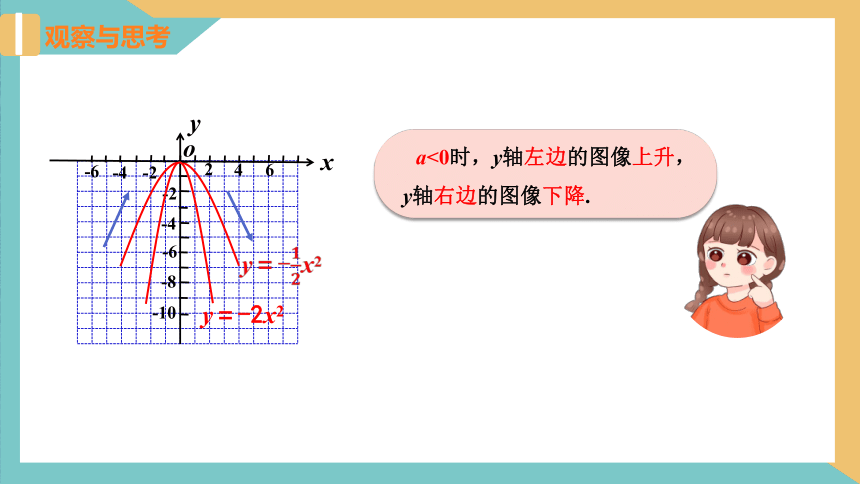
a<0时,y轴左边的图像上升,y轴右边的图像下降.
观察与思考
2. 如何用x、y的值的变化来描述图像的上升、下降?
图像“上升”可以用“x增大时,y也增大”来描述
图像“下降”可以用“x增大时,y减小”来描述.
归纳总结
二次函数y=ax2的图像的性质2:
(1)a>0,
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大;
当x=0时,y的值最小,最小值是0.
(2)a<0,
当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小;
当x=0时,y的值最大,最大值是0.
开口向上,左减右增
开口向下,左增右减
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
讨论与交流
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
-2
-8
-10
y=-2x2
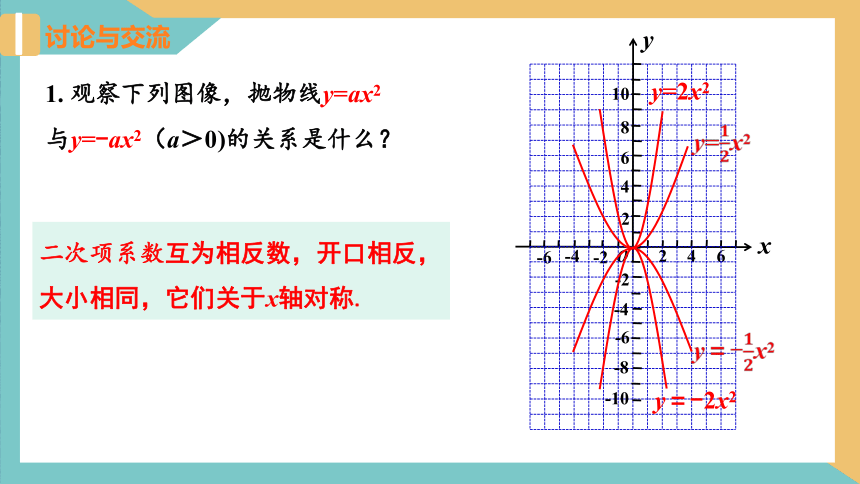
1. 观察下列图像,抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
讨论与交流
2. 从二次函数y=????????x2 、y=x2 、y=2x2 、y=-????????x2 、y=-x2 、y=-2x2 的图像看,
抛物线的开口大小与a有什么关系?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
-2
-8
-10
y=-2x2
y=x2
y=-x2
当a>0时,a越大,开口越小.
当a<0时,????越大,开口越小.
?
归纳总结
{5940675A-B579-460E-94D1-54222C63F5DA}y=ax2
a>0
a<0
图像
位置开
口方向
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴是y轴(直线x=0)
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小.
y
O
x
y
O
x
新知巩固
1.你能快速说出下列函数图像的开口方向、顶点坐标、对称轴、增减性、最大(小)值吗?
(1) y=-3x?;
(2) y=????????x? ;
(3) y=5x? ;
(4) y=-????????x? .
?
新知巩固
(1) 对于函数y=????????x2,当x<0时,y随x增大而______;当x>0时,y随x增大而______;当x=___时,y的值最____,最_____值是____.
?
减小
2. 填空:
增大
0
小
小
0
(2) 对于函数y=-7x2,当x<0时,y随x增大而______;当x>0时,y随x增大而______;当x=___时,y的值最____,最_____值是____.
增大
减小
0
大
大
0
新知巩固
3. 如图,在同一平面直角坐标系中,作出函数①y=3x2;②y=????????x2;③y=x2的图像,则从里到外的三条抛物线对应的函数依次是( )
A.①②③ B.①③② C.②③① D.③②①
?
B
例1 已知函数y=(m+3)????????????+?????????????是关于x的二次函数.
(1)求m的值;
?
解:(1)∵函数y=(m+3)????????????+?????????????是关于x的二次函数,
∴m?+3m-2=2,且m+3≠0,
解得m1=-4,m2=1.
?
例题讲解
(2)当m为何值时,该函数图像的开口向下?
解:(2)函数图像的开口向下,
∴m+3<0,∴m<-3,
∴当m=-4时,该函数图像的开口向下.
(3)当m为何值时,该函数有最小值?
(3)∵当m+3>0时,抛物线有最低点,函数有最小值,∴m>-3,
∴当m=1时,该函数有最小值.
例题讲解
例2 函数y=ax?(a≠0)与直线y=2x-3交于点A(1,b).
求:(1)a与b的值.
(2)求抛物线y=ax?的解析式,并写出顶点坐标和对称轴.
解:(1)将A(1,b)代入y=2x-3,得b=-1;将A(1,-1)代入y=ax?(a≠0),得a=-1.
(2) 抛物线y=-x?,顶点坐标(0,0),对称轴是y轴.
例题讲解
拓展延伸
例3 函数y=ax2(a>0)的图像上有A(2,y1),B(3,y2),C(-1,y3)三个点,比较y1,y2,y3的大小.
解:方法一:由题意知y1=4a,y2=9a,y3=a.
又∵a>0,∴y3方法二:∵函数y=ax2(a>0)的图像是一条抛物线,且关于y轴对称,点C(-1,y3)在该抛物线上,
∴点(1,y3)也在函数y=ax2(a>0)的图像上.
∵a>0,∴当x>0时,y随x的增大而增大.
又∵1<2<3,
∴y3归纳总结
比较抛物线上多个点的纵坐标的大小,可以先比较各点到对称轴的距离.
若抛物线开口向上,则离对称轴越近的点的纵坐标越小;
若抛物线开口向下,则离对称轴越近的点的纵坐标越大.
比较抛物线上多个点纵坐标大小的方法:
新知巩固
2.若A(x1,y1),B(x2,y2)在这条抛物线上,且x1>
1.已知y=(k+2)????????????+?????????是二次函数,且当x>0时,y随x增大而增大,则k=___.
?
2
3.已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y = ????????????????上,则y1、y2、y3的大小关系是______________.
?
y2<y3<y1
课堂小结
二次函数y=ax2的性质
开口方向
顶点坐标
对称轴
增减性
1. 关于函数y=2x2的性质的叙述,错误的是 ( )
A.对称轴是y轴 B.顶点是原点
C.当x>0时,y随x的增大而增大 D.y有最大值
D
2. 下列函数中,当x>0时y值随x值增大而减小的是 ( )
A. y=x2 B. y=x-1 C. y=????????x D. y=????????
?
D
当堂检测
当堂检测
3.下列说法错误的是( ) A. 二次函数y=3x2中,当x>0时,y随x的增大而增大 B. 二次函数y=-6x2中,当x=0时,y有最大值为0 C. a越大图像开口越小,a越小图像开口越大 B. 不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
C
当堂检测
4. 如图,当ab>0时,函数y=ax2与函数y=bx+a的图像大致是( )
C
当堂检测
5.若抛物线y=ax2 (a ≠ 0),过点(-1,2).
(1)则a的值是_____;
(2)对称轴是________,开口__________.
(3)顶点坐标是_________,顶点是抛物线上的最_____值 .
(4)抛物线在x轴的_____方(除顶点外).
2
y轴
向上
(0,0)
小
上
当堂检测
6.已知一个二次函数,满足下列条件:①顶点为原点;②当x>0时,函数值y随着x的增大而减小.请写出一个函数表达式:___________________.
(写出一个即可)
答案不唯一,如y=-x2
7.如下图,观察函数y=( k-1)x2的图像,则k的取值范围是________.
k>1
x
y
O
8.如图所示的四个二次函数的图像中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2,则a,b,c,d的大小关系为__________.(用“>”连接)
a>b>d>c
当堂检测
当堂检测
9. 已知y=(k+3)????????????+?????????是二次函数,且当x>0时,y随x的增大而增大.
(1)求k的值;
(2)求顶点坐标和对称轴.
?
解:(1)由????????+?????????=????????+????>???? ,解得k=2;
?
(2)顶点坐标为(0,0),对称轴为y轴.
5.2 二次函数的图像和性质(2)
第2课时 二次函数y=ax2性质
学习目标
1.能归纳总结y=ax?(a≠0)的图像性质;
2.体会数形结合的思想方法.
观察与思考
观察上节课所画的函数 y=????????x2、 y=2x2、 y=-2x2、y=-????????x2的图像,它们有什么共同的特征,有什么不同的地方?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
小组讨论交流
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
这两个函数的图像都是抛物线,抛物线的开口向上,对称轴是y轴,顶点在原点,顶点是抛物线的最低点.
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
这两个函数的图像都是抛物线,抛物线的开口向下,对称轴是y轴,顶点在原点,顶点是抛物线的最高点.
归纳总结
二次函数y=ax2的图像的性质1:
(1)二次函数y=ax?的图像是一条抛物线,抛物线的顶点在原点,对称轴为y轴.
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最低点.
(3)当a<0时,抛物线的开口向下,顶点是抛物线的最高点.
思考与探索
1. 观察y=ax?图像的变化趋势,你还能发现什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
小组讨论交流
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
a>0时,y轴左边的图像下降,
y轴右边的图像上升.
观察与思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
x
y
2
4
-2
-4
o
6
-6
-2
-8
-10
y=-2x2
a<0时,y轴左边的图像上升,y轴右边的图像下降.
观察与思考
2. 如何用x、y的值的变化来描述图像的上升、下降?
图像“上升”可以用“x增大时,y也增大”来描述
图像“下降”可以用“x增大时,y减小”来描述.
归纳总结
二次函数y=ax2的图像的性质2:
(1)a>0,
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大;
当x=0时,y的值最小,最小值是0.
(2)a<0,
当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小;
当x=0时,y的值最大,最大值是0.
开口向上,左减右增
开口向下,左增右减
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
讨论与交流
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
-2
-8
-10
y=-2x2
1. 观察下列图像,抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
讨论与交流
2. 从二次函数y=????????x2 、y=x2 、y=2x2 、y=-????????x2 、y=-x2 、y=-2x2 的图像看,
抛物线的开口大小与a有什么关系?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=2x2
y=????????x2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=-????????x2
?
-6
-4
-2
-8
-10
y=-2x2
y=x2
y=-x2
当a>0时,a越大,开口越小.
当a<0时,????越大,开口越小.
?
归纳总结
{5940675A-B579-460E-94D1-54222C63F5DA}y=ax2
a>0
a<0
图像
位置开
口方向
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴是y轴(直线x=0)
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小.
y
O
x
y
O
x
新知巩固
1.你能快速说出下列函数图像的开口方向、顶点坐标、对称轴、增减性、最大(小)值吗?
(1) y=-3x?;
(2) y=????????x? ;
(3) y=5x? ;
(4) y=-????????x? .
?
新知巩固
(1) 对于函数y=????????x2,当x<0时,y随x增大而______;当x>0时,y随x增大而______;当x=___时,y的值最____,最_____值是____.
?
减小
2. 填空:
增大
0
小
小
0
(2) 对于函数y=-7x2,当x<0时,y随x增大而______;当x>0时,y随x增大而______;当x=___时,y的值最____,最_____值是____.
增大
减小
0
大
大
0
新知巩固
3. 如图,在同一平面直角坐标系中,作出函数①y=3x2;②y=????????x2;③y=x2的图像,则从里到外的三条抛物线对应的函数依次是( )
A.①②③ B.①③② C.②③① D.③②①
?
B
例1 已知函数y=(m+3)????????????+?????????????是关于x的二次函数.
(1)求m的值;
?
解:(1)∵函数y=(m+3)????????????+?????????????是关于x的二次函数,
∴m?+3m-2=2,且m+3≠0,
解得m1=-4,m2=1.
?
例题讲解
(2)当m为何值时,该函数图像的开口向下?
解:(2)函数图像的开口向下,
∴m+3<0,∴m<-3,
∴当m=-4时,该函数图像的开口向下.
(3)当m为何值时,该函数有最小值?
(3)∵当m+3>0时,抛物线有最低点,函数有最小值,∴m>-3,
∴当m=1时,该函数有最小值.
例题讲解
例2 函数y=ax?(a≠0)与直线y=2x-3交于点A(1,b).
求:(1)a与b的值.
(2)求抛物线y=ax?的解析式,并写出顶点坐标和对称轴.
解:(1)将A(1,b)代入y=2x-3,得b=-1;将A(1,-1)代入y=ax?(a≠0),得a=-1.
(2) 抛物线y=-x?,顶点坐标(0,0),对称轴是y轴.
例题讲解
拓展延伸
例3 函数y=ax2(a>0)的图像上有A(2,y1),B(3,y2),C(-1,y3)三个点,比较y1,y2,y3的大小.
解:方法一:由题意知y1=4a,y2=9a,y3=a.
又∵a>0,∴y3
∴点(1,y3)也在函数y=ax2(a>0)的图像上.
∵a>0,∴当x>0时,y随x的增大而增大.
又∵1<2<3,
∴y3
比较抛物线上多个点的纵坐标的大小,可以先比较各点到对称轴的距离.
若抛物线开口向上,则离对称轴越近的点的纵坐标越小;
若抛物线开口向下,则离对称轴越近的点的纵坐标越大.
比较抛物线上多个点纵坐标大小的方法:
新知巩固
2.若A(x1,y1),B(x2,y2)在这条抛物线上,且x1
1.已知y=(k+2)????????????+?????????是二次函数,且当x>0时,y随x增大而增大,则k=___.
?
2
3.已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y = ????????????????上,则y1、y2、y3的大小关系是______________.
?
y2<y3<y1
课堂小结
二次函数y=ax2的性质
开口方向
顶点坐标
对称轴
增减性
1. 关于函数y=2x2的性质的叙述,错误的是 ( )
A.对称轴是y轴 B.顶点是原点
C.当x>0时,y随x的增大而增大 D.y有最大值
D
2. 下列函数中,当x>0时y值随x值增大而减小的是 ( )
A. y=x2 B. y=x-1 C. y=????????x D. y=????????
?
D
当堂检测
当堂检测
3.下列说法错误的是( ) A. 二次函数y=3x2中,当x>0时,y随x的增大而增大 B. 二次函数y=-6x2中,当x=0时,y有最大值为0 C. a越大图像开口越小,a越小图像开口越大 B. 不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
C
当堂检测
4. 如图,当ab>0时,函数y=ax2与函数y=bx+a的图像大致是( )
C
当堂检测
5.若抛物线y=ax2 (a ≠ 0),过点(-1,2).
(1)则a的值是_____;
(2)对称轴是________,开口__________.
(3)顶点坐标是_________,顶点是抛物线上的最_____值 .
(4)抛物线在x轴的_____方(除顶点外).
2
y轴
向上
(0,0)
小
上
当堂检测
6.已知一个二次函数,满足下列条件:①顶点为原点;②当x>0时,函数值y随着x的增大而减小.请写出一个函数表达式:___________________.
(写出一个即可)
答案不唯一,如y=-x2
7.如下图,观察函数y=( k-1)x2的图像,则k的取值范围是________.
k>1
x
y
O
8.如图所示的四个二次函数的图像中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2,则a,b,c,d的大小关系为__________.(用“>”连接)
a>b>d>c
当堂检测
当堂检测
9. 已知y=(k+3)????????????+?????????是二次函数,且当x>0时,y随x的增大而增大.
(1)求k的值;
(2)求顶点坐标和对称轴.
?
解:(1)由????????+?????????=????????+????>???? ,解得k=2;
?
(2)顶点坐标为(0,0),对称轴为y轴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
