5.2 二次函数的图像和性质(第3课时)课件(共27张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 5.2 二次函数的图像和性质(第3课时)课件(共27张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 19:25:54 | ||
图片预览


文档简介
(共27张PPT)
第5章 二次函数
5.2 二次函数的图像和性质(3)
第3课时 二次函数y=ax2+k的图像和性质
学习目标
1.会用描点法画函数y=ax2+k(a≠0)的图像;
2.能用平移变换解释二次函数y=ax2+k二次函数y=ax2(a≠0)的位置关系;
3.能根据图像认识和理解二次函数 y=ax2+k(a≠0)的性质.
知识回顾
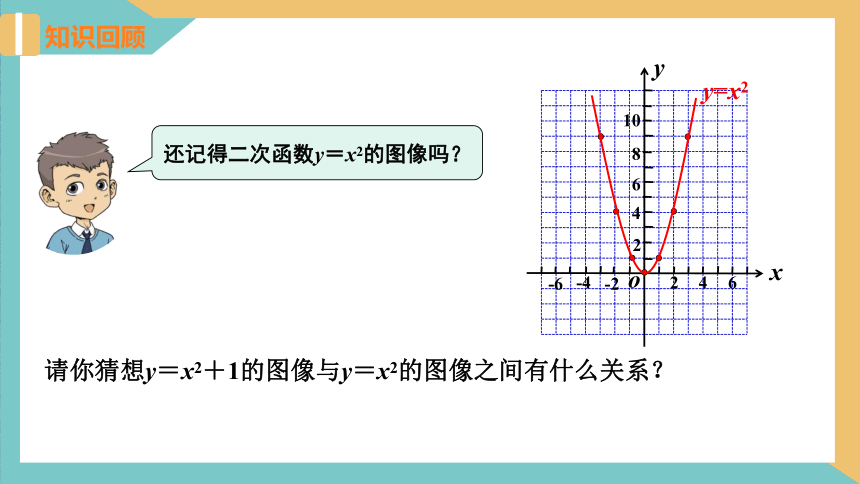
还记得二次函数y=x2的图像吗?
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
请你猜想y=x2+1的图像与y=x2的图像之间有什么关系?
思考与探索
在同一坐标系中画出函数y=x2和y=x2+1的图像.
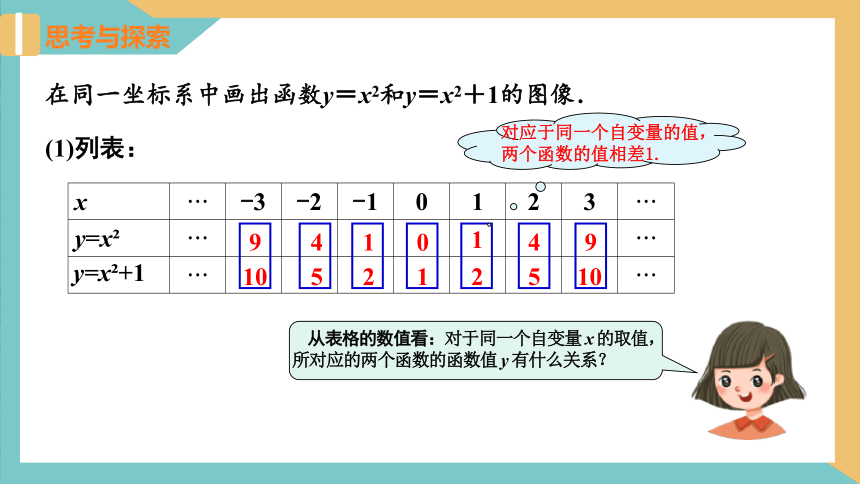
(1)列表:
x -3 -2 -1 0 1 2 3
y=x
9
4
1
0
1
9
4
y=x +1
10
5
2
1
2
10
5
从表格的数值看:对于同一个自变量 x 的取值,所对应的两个函数的函数值 y 有什么关系?
对应于同一个自变量的值,两个函数的值相差1.
思考与探索
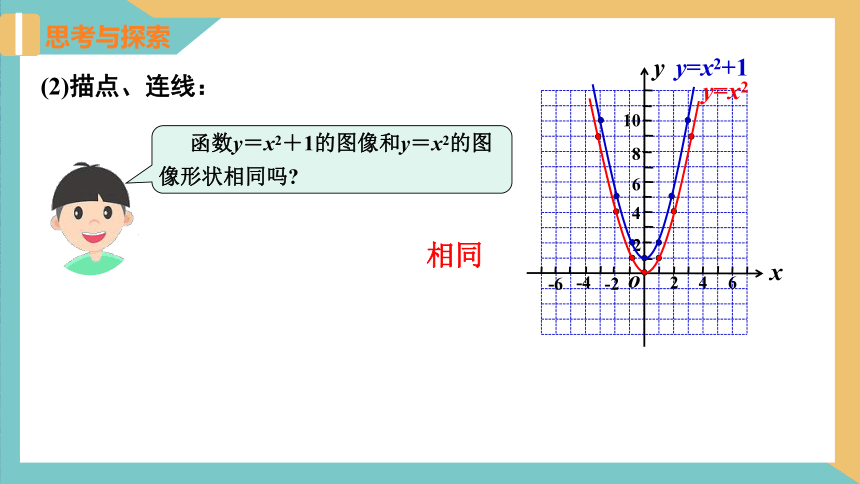
(2)描点、连线:
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
函数y=x2+1的图像和y=x2的图像形状相同吗
相同
y=x2+1
思考与探索
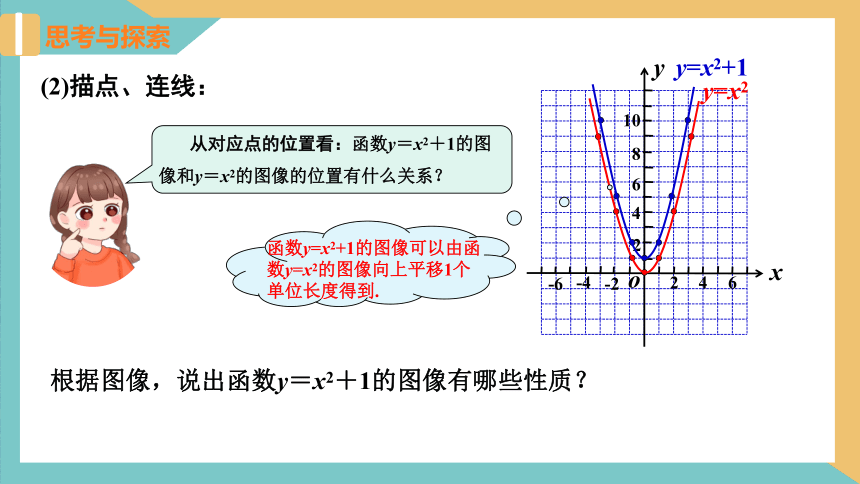
(2)描点、连线:
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
y=x2+1
从对应点的位置看:函数y=x2+1的图像和y=x2的图像的位置有什么关系?
函数y=x2+1的图像可以由函数y=x2的图像向上平移1个单位长度得到.
根据图像,说出函数y=x2+1的图像有哪些性质?
思考与探索
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
y=x2+1
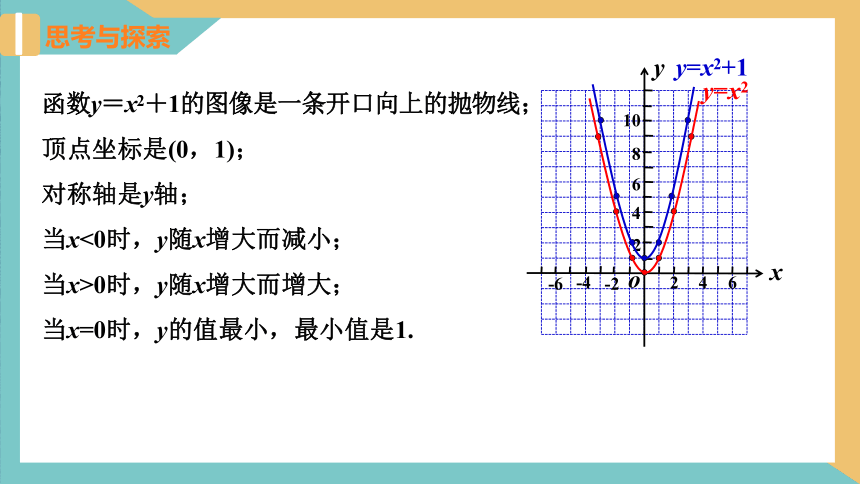
函数y=x2+1的图像是一条开口向上的抛物线;
顶点坐标是(0,1);
对称轴是y轴;
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大;
当x=0时,y的值最小,最小值是1.
思考与探索
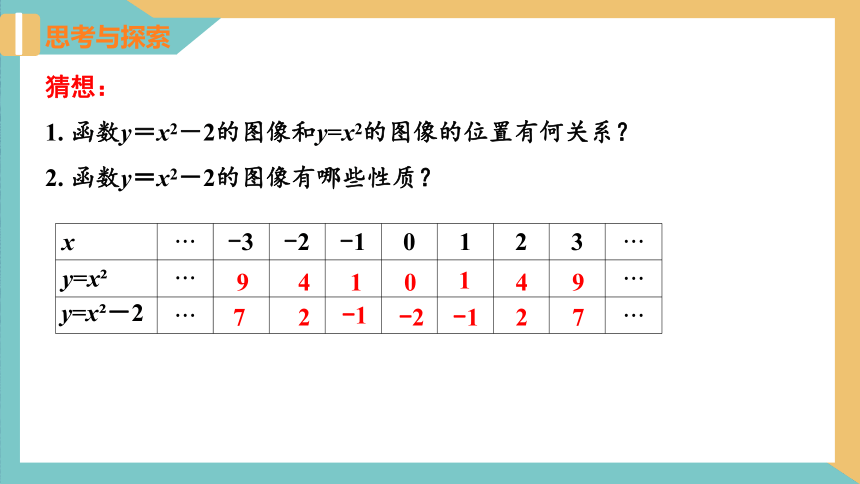
猜想:
1. 函数y=x2-2的图像和y=x2的图像的位置有何关系?
2. 函数y=x2-2的图像有哪些性质?
x -3 -2 -1 0 1 2 3
y=x
9
4
1
0
1
9
4
y=x -2
7
2
-1
-2
-1
7
2
思考与探索
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
y=x2+1
y=x2-2
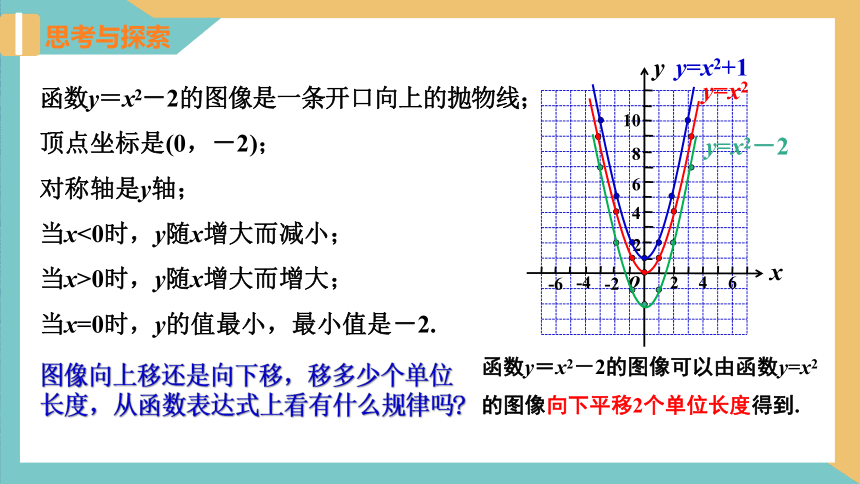
函数y=x2-2的图像是一条开口向上的抛物线;
顶点坐标是(0,-2);
对称轴是y轴;
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大;
当x=0时,y的值最小,最小值是-2.
函数y=x2-2的图像可以由函数y=x2的图像向下平移2个单位长度得到.
图像向上移还是向下移,移多少个单位长度,从函数表达式上看有什么规律吗
新知应用
在同一直角坐标系中,画出二次函数 y=2x , y=2x2+1 ,y=2x2-1的图像.
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2+1 … …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2-1 … …
3.5
1
-0.5
1
-0.5
-1
3.5
5.5
1.5
3
1.5
1
3
5.5
解:列表:
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
新知应用
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
根据图像填空:
把抛物线y=2x2 向_____平移1个单位长度,就得到抛物线 ______;
把抛物线 y=2x2 向_____平移1个单位长度,就得到抛物线 y=2x2-1.
上
y=2x2+1
下
新知应用
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
根据图像回答下列问题:
(1)图像的形状都是_________;
(2)三条抛物线的开口方向_______;
(3)对称轴都是_______;
(4)从上而下顶点坐标分别是_______________________;
(5)顶点都是最____点,函数都有最____值,从上而下最小值分别为_____、_____﹑______;
(6) 函数的增减性都相同:_________________________
___________________________.
抛物线
向上
y轴
( 0,1),( 0,0),( 0,-1)
低
小
1
0
-1
对称轴左侧y随x增大而减小
对称轴右侧y随x增大而增大
平移中的“变”与“不变”
抛物线上下平移后,开口的大小和方向不变,即a的值不变,顶点的横坐标不变,纵坐标发生变化.
函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图像形状________,只是位置不同;
当k>0时,函数y=ax2+k的图像可由y=ax2的图像向____平移____个单位得到,
当k<0时,函数y=ax2+k的图像可由y=ax2的图像向 ____平移____个单位得到.
二次函数y=ax2 与y=ax2+k(a ≠ 0)的图像的关系
归纳总结
相同
上
k
下
|k|
平移规律:上加下减
归纳总结
二次函数y=ax2+k(a ≠ 0)的性质:
y=ax2+k a>0 a<0
开口方向 向上 向下
对称轴 y轴 y轴
顶点坐标 (0,k) (0,k)
最值 当x=0时,y最小值=k 当x=0时,y最大值=k
增减性 当x<0时,y随x的增大而减小;x>0时,y随x的增大而增大. 当x>0时,y随x的增大而减小;x<0时,y随x的增大而增大.
新知巩固
1. 二次函数y=-3x2+1的图像是将( )
A. 抛物线y=-3x2向左平移3个单位得到
B. 抛物线y=-3x2向左平移1个单位得到
C. 抛物线y=3x2向上平移1个单位得到
D. 抛物线y=-3x2向上平移1个单位得到
D
2. 抛物线y=2x2向下平移4个单位,就得到抛物线_____________;
抛物线y=x2+1可由抛物线y=x2-1______________________得到.
y = 2x2-4
向上平移2个单位长度
新知巩固
3.抛物线y=-3x2+5的开口______,对称轴是_____,顶点坐标是______,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,当x=___时,取得最____值,这个值等于___.
向下
y轴
(0,5)
减小
增大
0
大
5
4.抛物线y=7x2-3的开口______,对称轴是_____,顶点坐标是_______,在对称轴的左侧,y随x的增大而_______,在对称轴的右侧,y随x的增大而_______,当x=____时,取得最___值,这个值等于____.
向上
y轴
(0,-3)
减小
增大
0
小
-3
新知巩固
5.不画函数y=-x2和y=-x2+1的图像回答下面的问题:
(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.
(2)函数y=-x2+1,当x_____时, y随x的增大而减小;当x_____时,函数y有最大值,最大值y是___,其图像与y轴的交点坐标是______,与x轴的交点坐标是_________________.
(3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.
向下平移1个单位.
>0
=0
1
(0,1)
(-1,0),(1,0)
开口方向向上,对称轴是y轴,顶点坐标(0,-3).
讨论与交流
1.怎样画y=ax2+k(a ≠ 0)的图像?
第一种方法:平移法,两步即第一步画y=ax2的图象,再向上(或向下)平移︱k︱单位.
第二种方法:描点法,三步即列表、描点和连线.
2.抛物线y=ax2+k 中的a决定什么?怎样决定的?k决定什么?它的对称轴是什么?顶点坐标怎样表示?
a决定开口方向和大小,k决定顶点的纵坐标.
课堂小结
二次函数y=ax2+k的图像和性质
与y=ax2的关系
图像
性质
上加下减
开口方向由a的符号决定
k决定顶点位置
对称轴是y轴
增减性结合开口方向和对称轴才能确定.
当堂检测
1.二次函数y=-x2+1的图像可能是( )
A B C D
D
当堂检测
2. 抛物线y=-6x2可以看作是由抛物线y=-6x2+5按下列何种变换得到( )
A.向上平移5个单位 B.向下平移5个单位
C.向左平移5个单位 D.向右平移5个单位
3.与抛物线y=-x2-1顶点相同,形状也相同而开口方向相反的抛物线所对应的函数是 ( )
A.y=-x2-1 B.y=x2-1 C.y=-x2-1 D.y=x2+1
B
B
当堂检测
4.抛物线y=2x2,y=-2x2-1,y=-x2+3共有的性质是( )
A.开口向上 B.顶点坐标都是(0,0)
C.对称轴是y轴 D.在对称轴的右侧,y随x的增大而增大
C
5.已知函数y=x2-2,当函数值y随x的增大而减小时,x的取值范围是( )
A.x<2 B.x>0 C.x>-2 D.x<0
D
当堂检测
6.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图像大致为( )
D
当堂检测
7.将抛物线y=-2x2向上平移4个单位长度,得到新的抛物线的函数表达式为____________,新抛物线的对称轴为_____,当x>0时,y随x的增大而______,当x=___时函数有最____值,最值为____.
y=-2x2+4
y轴
减小
0
大
4
8.如果点A(-4,y1),B(-3,y2)是二次函数y=2x2+k(k是常数)图像上的两点,那么y1________y2.(填“>”“<”或“=”)
>
当堂检测
9.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)则a=____.
-2
10.若y=x2+(k-2)的顶点是原点,则k____;若顶点位于x轴上方,则k____;若顶点位于x轴下方,则k .
=2
>2
<2
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±,
此时P点坐标为(,2),(-,2);
当b=-2时,x2-4=-2,解得x=±,
此时P点坐标为(,2),(-,2).
当堂检测
11.如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
当堂检测
12.如图,在平面直角坐标系xOy中,抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC的顶点A,B在此抛物线上,AB与y轴相交于点M.已知点C的坐标是(-4,0),点Q(x,y)是抛物线上任意一点.
求此抛物线的函数表达式及点M的坐标;
解:∵抛物线的顶点坐标是(0,1),
∴设其函数表达式为y=ax2+1.
∵抛物线过点(-2,2),
∴2=a×(-2)2+1,解得a=,
∴此抛物线的函数表达式为y=x2+1.
∵四边形OABC是平行四边形,
∴AB=OC=4,AB∥OC.
又∵y轴是该抛物线的对称轴,
∴点A与点B关于y轴对称,
∴MA=MB=2,即点A的横坐标是2,
则其纵坐标y=×22+1=2,即点A的坐标为(2,2),
故点M的坐标为(0,2).
第5章 二次函数
5.2 二次函数的图像和性质(3)
第3课时 二次函数y=ax2+k的图像和性质
学习目标
1.会用描点法画函数y=ax2+k(a≠0)的图像;
2.能用平移变换解释二次函数y=ax2+k二次函数y=ax2(a≠0)的位置关系;
3.能根据图像认识和理解二次函数 y=ax2+k(a≠0)的性质.
知识回顾
还记得二次函数y=x2的图像吗?
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
请你猜想y=x2+1的图像与y=x2的图像之间有什么关系?
思考与探索
在同一坐标系中画出函数y=x2和y=x2+1的图像.
(1)列表:
x -3 -2 -1 0 1 2 3
y=x
9
4
1
0
1
9
4
y=x +1
10
5
2
1
2
10
5
从表格的数值看:对于同一个自变量 x 的取值,所对应的两个函数的函数值 y 有什么关系?
对应于同一个自变量的值,两个函数的值相差1.
思考与探索
(2)描点、连线:
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
函数y=x2+1的图像和y=x2的图像形状相同吗
相同
y=x2+1
思考与探索
(2)描点、连线:
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
y=x2+1
从对应点的位置看:函数y=x2+1的图像和y=x2的图像的位置有什么关系?
函数y=x2+1的图像可以由函数y=x2的图像向上平移1个单位长度得到.
根据图像,说出函数y=x2+1的图像有哪些性质?
思考与探索
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
y=x2+1
函数y=x2+1的图像是一条开口向上的抛物线;
顶点坐标是(0,1);
对称轴是y轴;
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大;
当x=0时,y的值最小,最小值是1.
思考与探索
猜想:
1. 函数y=x2-2的图像和y=x2的图像的位置有何关系?
2. 函数y=x2-2的图像有哪些性质?
x -3 -2 -1 0 1 2 3
y=x
9
4
1
0
1
9
4
y=x -2
7
2
-1
-2
-1
7
2
思考与探索
2
4
-2
-4
o
2
4
x
y
6
-6
8
6
10
y=x2
y=x2+1
y=x2-2
函数y=x2-2的图像是一条开口向上的抛物线;
顶点坐标是(0,-2);
对称轴是y轴;
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大;
当x=0时,y的值最小,最小值是-2.
函数y=x2-2的图像可以由函数y=x2的图像向下平移2个单位长度得到.
图像向上移还是向下移,移多少个单位长度,从函数表达式上看有什么规律吗
新知应用
在同一直角坐标系中,画出二次函数 y=2x , y=2x2+1 ,y=2x2-1的图像.
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2+1 … …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2-1 … …
3.5
1
-0.5
1
-0.5
-1
3.5
5.5
1.5
3
1.5
1
3
5.5
解:列表:
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
新知应用
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
根据图像填空:
把抛物线y=2x2 向_____平移1个单位长度,就得到抛物线 ______;
把抛物线 y=2x2 向_____平移1个单位长度,就得到抛物线 y=2x2-1.
上
y=2x2+1
下
新知应用
x
y
O
-2
2
2
4
6
4
-4
8
y=2x2+1
y=2x2
y=2x2-1
根据图像回答下列问题:
(1)图像的形状都是_________;
(2)三条抛物线的开口方向_______;
(3)对称轴都是_______;
(4)从上而下顶点坐标分别是_______________________;
(5)顶点都是最____点,函数都有最____值,从上而下最小值分别为_____、_____﹑______;
(6) 函数的增减性都相同:_________________________
___________________________.
抛物线
向上
y轴
( 0,1),( 0,0),( 0,-1)
低
小
1
0
-1
对称轴左侧y随x增大而减小
对称轴右侧y随x增大而增大
平移中的“变”与“不变”
抛物线上下平移后,开口的大小和方向不变,即a的值不变,顶点的横坐标不变,纵坐标发生变化.
函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图像形状________,只是位置不同;
当k>0时,函数y=ax2+k的图像可由y=ax2的图像向____平移____个单位得到,
当k<0时,函数y=ax2+k的图像可由y=ax2的图像向 ____平移____个单位得到.
二次函数y=ax2 与y=ax2+k(a ≠ 0)的图像的关系
归纳总结
相同
上
k
下
|k|
平移规律:上加下减
归纳总结
二次函数y=ax2+k(a ≠ 0)的性质:
y=ax2+k a>0 a<0
开口方向 向上 向下
对称轴 y轴 y轴
顶点坐标 (0,k) (0,k)
最值 当x=0时,y最小值=k 当x=0时,y最大值=k
增减性 当x<0时,y随x的增大而减小;x>0时,y随x的增大而增大. 当x>0时,y随x的增大而减小;x<0时,y随x的增大而增大.
新知巩固
1. 二次函数y=-3x2+1的图像是将( )
A. 抛物线y=-3x2向左平移3个单位得到
B. 抛物线y=-3x2向左平移1个单位得到
C. 抛物线y=3x2向上平移1个单位得到
D. 抛物线y=-3x2向上平移1个单位得到
D
2. 抛物线y=2x2向下平移4个单位,就得到抛物线_____________;
抛物线y=x2+1可由抛物线y=x2-1______________________得到.
y = 2x2-4
向上平移2个单位长度
新知巩固
3.抛物线y=-3x2+5的开口______,对称轴是_____,顶点坐标是______,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,当x=___时,取得最____值,这个值等于___.
向下
y轴
(0,5)
减小
增大
0
大
5
4.抛物线y=7x2-3的开口______,对称轴是_____,顶点坐标是_______,在对称轴的左侧,y随x的增大而_______,在对称轴的右侧,y随x的增大而_______,当x=____时,取得最___值,这个值等于____.
向上
y轴
(0,-3)
减小
增大
0
小
-3
新知巩固
5.不画函数y=-x2和y=-x2+1的图像回答下面的问题:
(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.
(2)函数y=-x2+1,当x_____时, y随x的增大而减小;当x_____时,函数y有最大值,最大值y是___,其图像与y轴的交点坐标是______,与x轴的交点坐标是_________________.
(3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.
向下平移1个单位.
>0
=0
1
(0,1)
(-1,0),(1,0)
开口方向向上,对称轴是y轴,顶点坐标(0,-3).
讨论与交流
1.怎样画y=ax2+k(a ≠ 0)的图像?
第一种方法:平移法,两步即第一步画y=ax2的图象,再向上(或向下)平移︱k︱单位.
第二种方法:描点法,三步即列表、描点和连线.
2.抛物线y=ax2+k 中的a决定什么?怎样决定的?k决定什么?它的对称轴是什么?顶点坐标怎样表示?
a决定开口方向和大小,k决定顶点的纵坐标.
课堂小结
二次函数y=ax2+k的图像和性质
与y=ax2的关系
图像
性质
上加下减
开口方向由a的符号决定
k决定顶点位置
对称轴是y轴
增减性结合开口方向和对称轴才能确定.
当堂检测
1.二次函数y=-x2+1的图像可能是( )
A B C D
D
当堂检测
2. 抛物线y=-6x2可以看作是由抛物线y=-6x2+5按下列何种变换得到( )
A.向上平移5个单位 B.向下平移5个单位
C.向左平移5个单位 D.向右平移5个单位
3.与抛物线y=-x2-1顶点相同,形状也相同而开口方向相反的抛物线所对应的函数是 ( )
A.y=-x2-1 B.y=x2-1 C.y=-x2-1 D.y=x2+1
B
B
当堂检测
4.抛物线y=2x2,y=-2x2-1,y=-x2+3共有的性质是( )
A.开口向上 B.顶点坐标都是(0,0)
C.对称轴是y轴 D.在对称轴的右侧,y随x的增大而增大
C
5.已知函数y=x2-2,当函数值y随x的增大而减小时,x的取值范围是( )
A.x<2 B.x>0 C.x>-2 D.x<0
D
当堂检测
6.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图像大致为( )
D
当堂检测
7.将抛物线y=-2x2向上平移4个单位长度,得到新的抛物线的函数表达式为____________,新抛物线的对称轴为_____,当x>0时,y随x的增大而______,当x=___时函数有最____值,最值为____.
y=-2x2+4
y轴
减小
0
大
4
8.如果点A(-4,y1),B(-3,y2)是二次函数y=2x2+k(k是常数)图像上的两点,那么y1________y2.(填“>”“<”或“=”)
>
当堂检测
9.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)则a=____.
-2
10.若y=x2+(k-2)的顶点是原点,则k____;若顶点位于x轴上方,则k____;若顶点位于x轴下方,则k .
=2
>2
<2
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±,
此时P点坐标为(,2),(-,2);
当b=-2时,x2-4=-2,解得x=±,
此时P点坐标为(,2),(-,2).
当堂检测
11.如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
当堂检测
12.如图,在平面直角坐标系xOy中,抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC的顶点A,B在此抛物线上,AB与y轴相交于点M.已知点C的坐标是(-4,0),点Q(x,y)是抛物线上任意一点.
求此抛物线的函数表达式及点M的坐标;
解:∵抛物线的顶点坐标是(0,1),
∴设其函数表达式为y=ax2+1.
∵抛物线过点(-2,2),
∴2=a×(-2)2+1,解得a=,
∴此抛物线的函数表达式为y=x2+1.
∵四边形OABC是平行四边形,
∴AB=OC=4,AB∥OC.
又∵y轴是该抛物线的对称轴,
∴点A与点B关于y轴对称,
∴MA=MB=2,即点A的横坐标是2,
则其纵坐标y=×22+1=2,即点A的坐标为(2,2),
故点M的坐标为(0,2).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
