5.2 平面直角坐标系(第2课时)课件(共35张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 5.2 平面直角坐标系(第2课时)课件(共35张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 19:28:11 | ||
图片预览


文档简介
(共35张PPT)
第5章 · 平面直角坐标系
5.2 平面直角坐标系(2)
第2课时 图形变换和点的坐标变化
学习目标
1. 探索关于x轴、y轴对称的点的坐标规律;
2. 探索在平面直角坐标系内平移对点的坐标的影响;
3. 理解并掌握图形变换与点的坐标变化的对应关系.
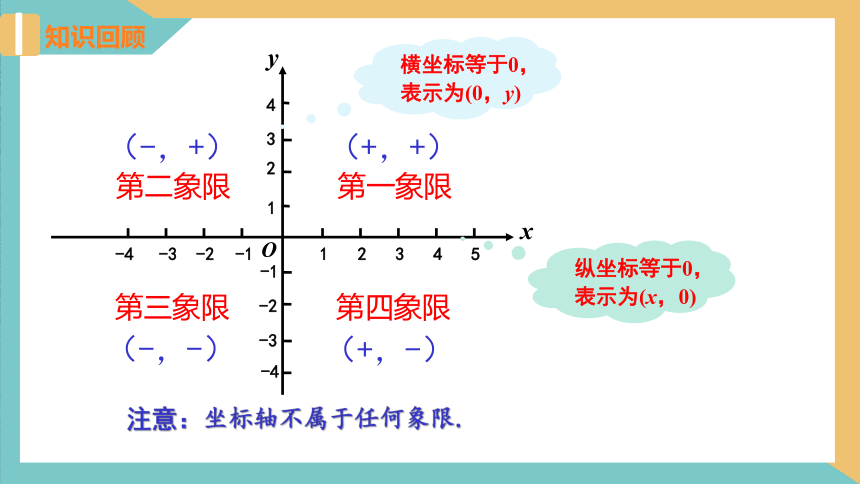
知识回顾
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
第四象限
第一象限
第二象限
第三象限
(+,+)
(-,+)
(-,-)
(+,-)
注意:坐标轴不属于任何象限.
纵坐标等于0,表示为(x,0)
横坐标等于0,表示为(0,y)
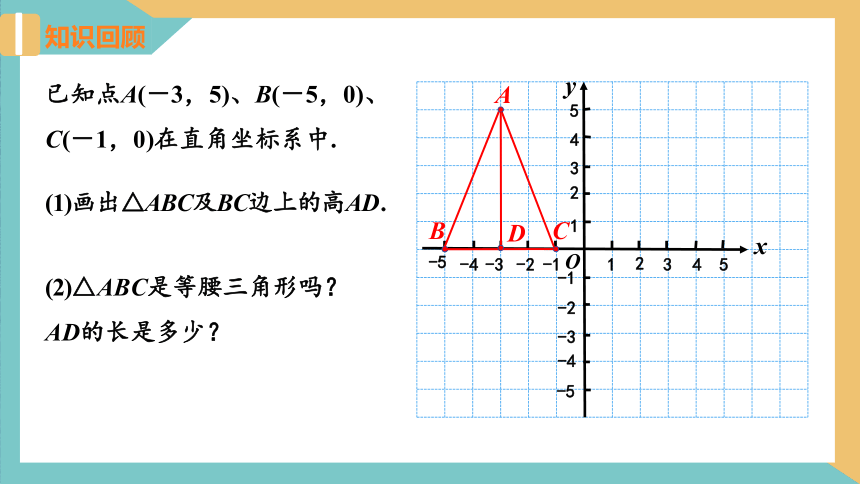
知识回顾
已知点A(-3,5)、B(-5,0)、C(-1,0)在直角坐标系中.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
C
-5
5
-5
B
(1)画出△ABC及BC边上的高AD.
(2)△ABC是等腰三角形吗?AD的长是多少?
A
D
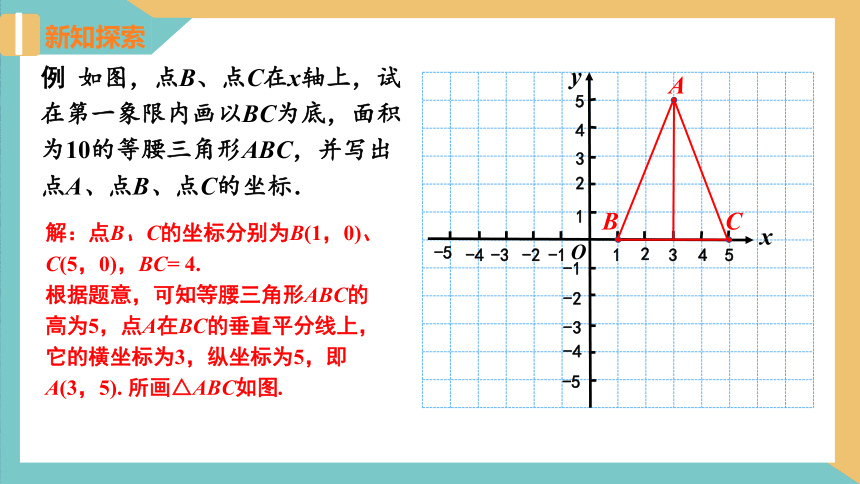
新知探索
例 如图,点B、点C在x轴上,试在第一象限内画以BC为底,面积为10的等腰三角形ABC,并写出点A、点B、点C的坐标.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
C
-5
5
-5
B
A
解:点B、C的坐标分别为B(1,0)、C(5,0),BC= 4.
根据题意,可知等腰三角形ABC的高为5,点A在BC的垂直平分线上,
它的横坐标为3,纵坐标为5,即A(3,5). 所画△ABC如图.
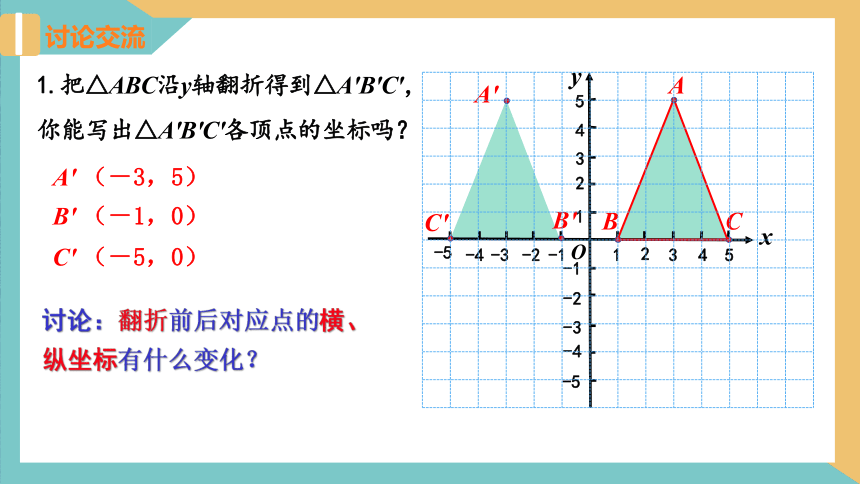
讨论交流
1.把△ABC沿y轴翻折得到△A′B′C′,你能写出△A′B′C′各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
C
5
B
A
A′
C′
B′
A′ (-3,5)
B′ (-1,0)
C′ (-5,0)
讨论:翻折前后对应点的横、纵坐标有什么变化?
讨论交流
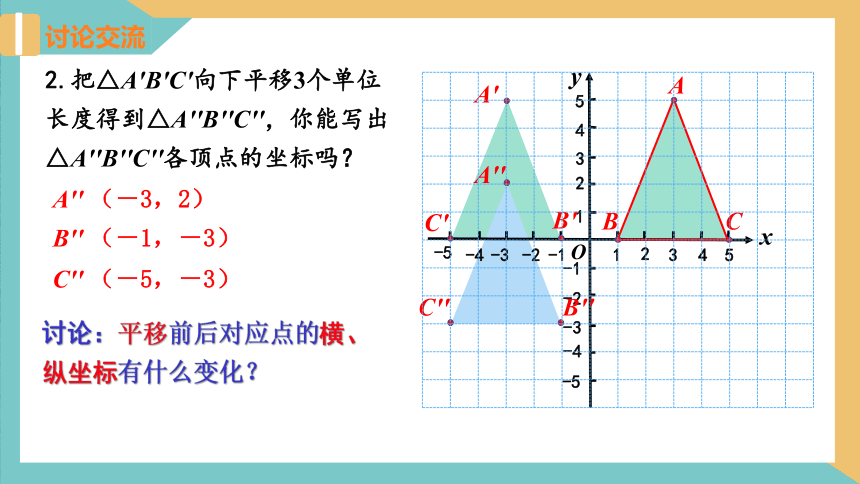
2.把△A′B′C′向下平移3个单位长度得到△A′′B′′C′′,你能写出△A′′B′′C′′各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
C
5
B
A
A′
C′
B′
A′′ (-3,2)
B′′ (-1,-3)
C′′ (-5,-3)
A′′
C′′
B′′
讨论:平移前后对应点的横、纵坐标有什么变化?
讨论交流
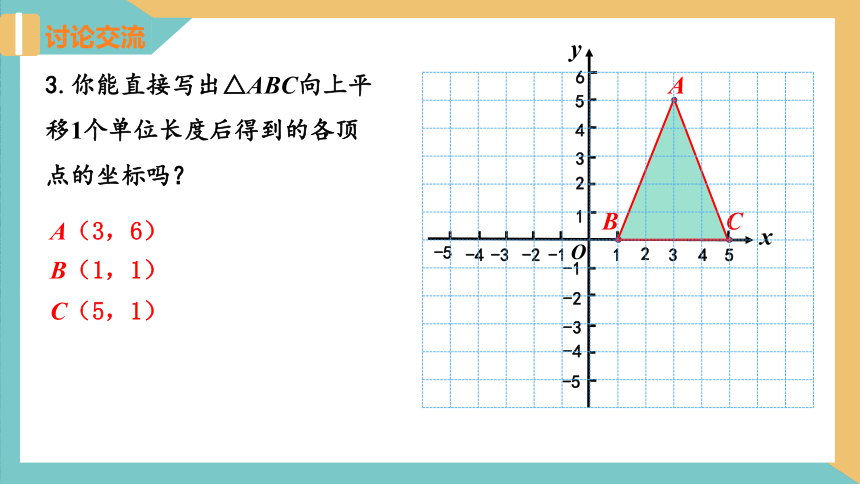
3.你能直接写出△ABC向上平移1个单位长度后得到的各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
5
A(3,6)
B(1,1)
C(5,1)
6
C
B
A
讨论交流
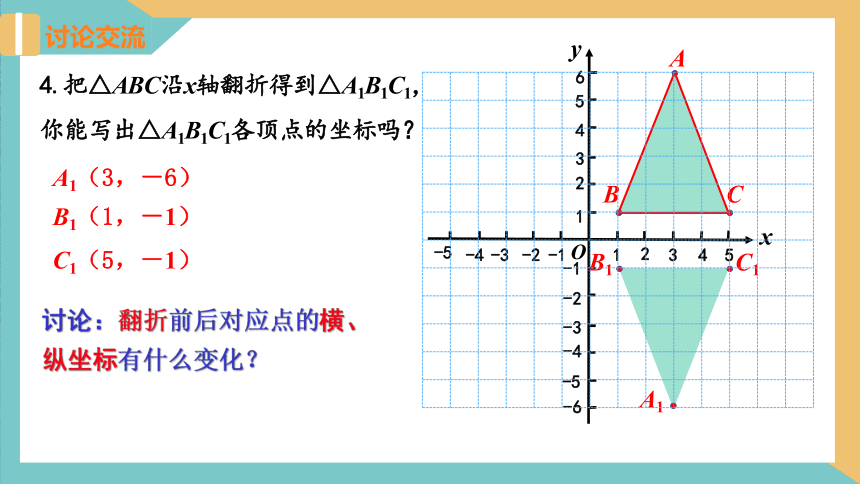
4.把△ABC沿x轴翻折得到△A1B1C1,你能写出△A1B1C1各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
5
6
C
B
A
A1
C1
B1
A1(3,-6)
B1(1,-1)
C1(5,-1)
讨论:翻折前后对应点的横、纵坐标有什么变化?
-6
数学实验室
O
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
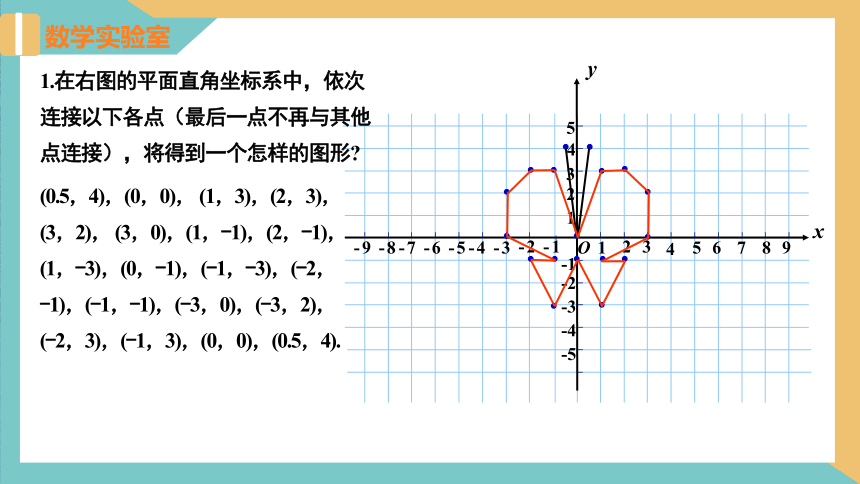
(0.5,4),(0,0), (1,3),(2,3), (3,2), (3,0),(1,-1),(2,-1),(1,-3),(0,-1),(-1,-3),(-2,-1),(-1,-1),(-3,0),(-3,2),
(-2,3),(-1,3),(0,0),(0.5,4).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1.在右图的平面直角坐标系中,依次连接以下各点(最后一点不再与其他点连接),将得到一个怎样的图形
数学实验室
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(1,3)
(-1,3)
(1,-3)
(-1,-3)
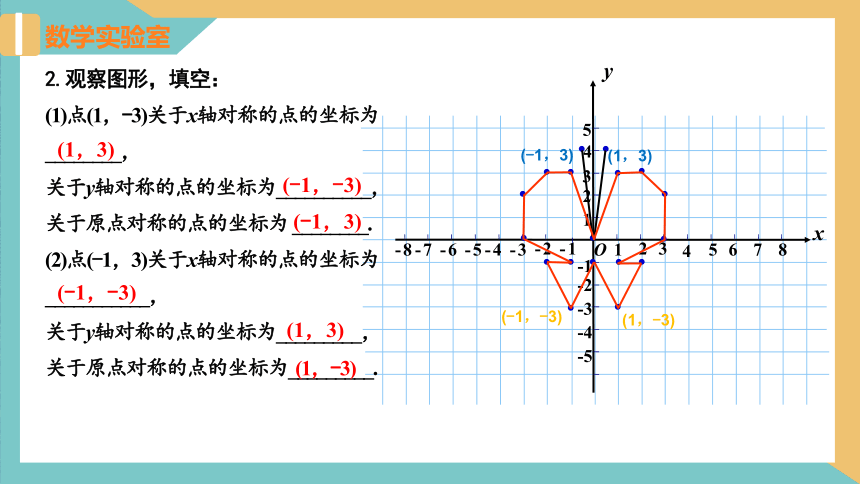
2.观察图形,填空:
(1)点(1,-3)关于x轴对称的点的坐标为________,
关于y轴对称的点的坐标为__________,
关于原点对称的点的坐标为 ________.
(2)点(-1,3)关于x轴对称的点的坐标为___________,
关于y轴对称的点的坐标为_________,
关于原点对称的点的坐标为_________.
(1,3)
(-1,-3)
(-1,3)
(1,3)
(-1,-3)
(1,-3)
数学实验室
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
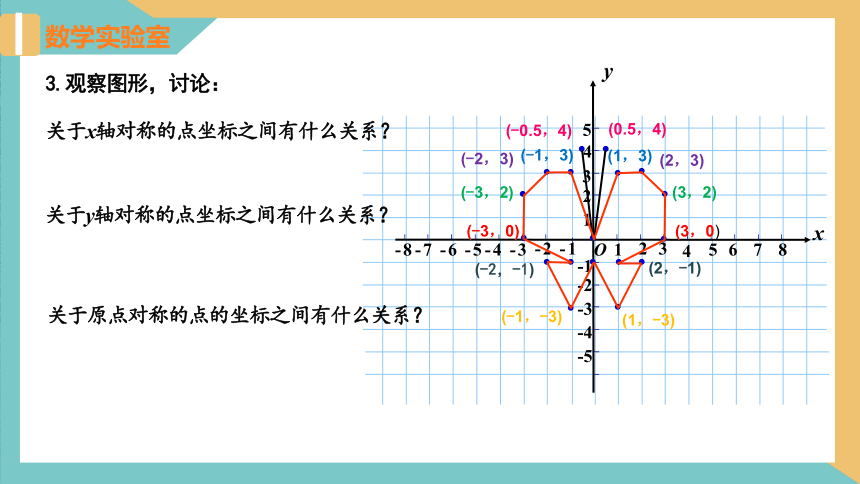
(3,0)
(-3,0)
(3,2)
(-3,2)
(2,3)
(-2,3)
(1,3)
(-1,3)
(1,-3)
(-1,-3)
(-2,-1)
(2,-1)
(0.5,4)
(-0.5,4)
3.观察图形,讨论:
关于原点对称的点的坐标之间有什么关系?
关于y轴对称的点坐标之间有什么关系?
关于x轴对称的点坐标之间有什么关系?
新知归纳
关于坐标轴对称的点的坐标特征:
(1)关于x轴对称的两个点,横坐标相等,纵坐标互为相反数.
点P(a , b)关于x轴对称点的坐标为(a,-b)
(2)关于y轴对称的两个点,纵坐标相等,横坐标互为相反数.
点P(a , b)关于y轴对称点的坐标为(-a,b)
拓展:点P(a , b)关于原点对称点的坐标为(-a,-b)
数学实验室
4. 在图中,把线段AB先向右平移7个单位长度,再向上平移2个单位长度,得到线段 A'B'.试分别写出点 A、B、A'、B'的坐标.
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
(1)你能说出点A与点A'、点B与点B'的坐标之间的关系吗
A(-4,1)
B(-2,3)
(3,1)
(5,3)
(3,3)A′
B′(5,5)
.
.
.
.
数学实验室
4. 在图中,把线段AB先向右平移7个单位长度,再向上平移2个单位长度,得到线段 A'B'.试分别写出点 A、B、A'、B'的坐标.
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
(2)如果点 C(m,n)是线段AB上的任意一点,那么当AB平移到A'B后,写出与点C对应的点C'的坐标.
A(-4,1)
B(-2,3)
(3,1)
(5,3)
(3,3)A′
B′(5,5)
.
.
.
.
(m+7, n+2)
讨论交流
2. 已知点A(a,b),B(a,c),且a≠0,b≠c,那么直线AB与坐标轴有什么位置关系?
3. 已知点C(b,d),D(c,d),且d≠0,b≠c,那么直线CD与坐标轴有什么位置关系?
1. 点的横坐标变化,纵坐标不变 , 点的位置发生了什么变化?点的纵坐标变化 ,横坐标不变呢?
新知归纳
点平移时坐标的变化规律:
(1)左右平移:纵坐标不变,横坐标左减右加;
(2)上下平移:横坐标不变,纵坐标上加下减.
与坐标轴平行的直线上的点的坐标特征:
平行于x轴的直线上的点纵坐标都相等;
平行于y轴的直线上的点横坐标都相等.
例题讲解
例 如图,图②至图④中的图形均是由图①中的图形变换得到的.
(1)请分别写出图①中点A、B、M、N的坐标;
(2)请分别写出图②至图④中与点A、B、M、N对应的点A'、B'、M'、
N'的坐标.
例题讲解
解: (1)A(2,4),B(4,0),M(1,2),N(3,2).
(2)图②中:A'(5,4),B'(7,0),M'(4,2),N'(6,2);
图③中:A'(2,-4),B'(4,0),M'(1,-2),N'(3,-2);
图④中:A'(4,8),B'(6,4),M'(3,6),N'(5,6).
1.平行于 x 轴的直线上不同的两个点的__坐标相同,__坐标不同;平行于 y 轴的直线上不同的两个点的 __坐标相同,__坐标不同.
新知巩固
2.点 P (a,b),关于 x 轴对称的点的坐标为________,关于 y 轴对称的点的坐标为________ .
3.图形左右平移,对应点的__坐标变化,__坐标不变;图形上下平移,对应点的__坐标变化,__坐标不变.
纵
横
横
纵
(a,-b)
(-a,b)
横
纵
纵
横
新知巩固
5.若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n= .
0
4. 在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是_______;
(-2,3)
6. 在平面直角坐标系中,将点P向右平移2个单位长度,再向下平移2个单位长度得点P′(-3,2),则点P的坐标为__________.
(-5,4)
7.(1)写出图①中点A、B、M、N的坐标;
新知巩固
解:(1) A(2,3),B(3,0),M(1,1.5),N(2.5,1.5);
(2)指出图①经过怎样的运动可以得到图②、图③、图④,并分别写出这 3个图中与点 A、B、M、N对应的点 A'、B'、M'、N'的坐标.
新知巩固
解:(2) 图②中:A' (4,3),B' (5,0), M'(3,1.5),N'(4.5,1.5);
新知巩固
图③中:A'(2,-3),B' (3,0), M'(1,-1.5),N'(2.5,-1.5);
图④中:A' (3,-2),B'(0,-3), M'(1.5,-1),N'(1.5,-2.5).
新知巩固
课堂小结
平面直角坐标系
关于坐标轴对称的点的坐标特征
点平移时坐标的变化规律
与坐标轴平行的直线上的点的坐标特征
当堂检测
2. 若点A(a,-1)与点B(2,b)关于y轴对称,则a-b的值是( )
A. -1 B. -3 C. 1 D. 2
1. 点A(2,-2)关于x轴对称的点的坐标为( )
A. (-2,2) B. (-2,-2) C. (2,2) D. (2,-2)
C
A
当堂检测
4. 将某图形的各顶点的横坐标保持不变,纵坐标减去3,可将该图形( )
A. 横向向右平移3个单位长度 B. 横向向左平移3个单位长度
C. 纵向向上平移3个单位长度 D. 纵向向下平移3个单位长度
3.在平面直角坐标系中,已知点A的坐标是(3,a),将点A向下平移4个单位长度得到点A′.若点A与点A′关于x轴对称,则a的值为( )
A.-2 B.2 C.-1 D.1
B
D
新知巩固
5. 四盏灯笼的位置如图.已知A、B、C、D的坐标分别是 ( 1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )
A. 将B向左平移4.5个单位
B. 将C向左平移4个单位
C. 将D向左平移5.5个单位
D. 将C向左平移3.5个单位
C
新知巩固
6.若点P(3m-12,2-m)在第三象限,且m为整数,则点P关于x轴对称的点的坐标为__________.
(-3,1)
7.在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是___________.
(-1,-2)
当堂检测
8. 已知P(a+1,b-2),Q(4,3)两点.
(1)若P,Q两点关于x轴对称,求a+b的值;
解:∵P,Q两点关于x轴对称,
∴a+1=4,b-2=-3,
∴a=3,b=-1,
∴a+b=3-1=2.
当堂检测
8. 已知P(a+1,b-2),Q(4,3)两点.
(2)若点P到y轴的距离是3,且PQ∥x轴,求点P的坐标.
解:∵点P到y轴的距离是3,
∴点P的横坐标为3或-3.
又∵PQ∥x轴,
∴点P的纵坐标为3,
∴点P的坐标为(3,3)或(-3,3).
当堂检测
9.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.已知A(1,3),A1(-2,-3),A2(4,3),A3(-8,-3),B(2,0),B1(-4,0),B2(8,0),B3(-16,0).
当堂检测
(1)观察每次变换前后的三角形有何变化,找出其中的规律,按此变化规律再将△OA3B3变换成△OA4B4,则点A4的坐标为________,点B4的坐标为________;
(16,3)
(32,0)
当堂检测
(2)若按第(1)题找到的规律将△OAB进行了n次变换,得到△OAnBn,推测点An的坐标为_________________,点Bn的坐标为_______________.
((-1)n·2n,(-1)n·3)
((-1)n·2n+1,0)
第5章 · 平面直角坐标系
5.2 平面直角坐标系(2)
第2课时 图形变换和点的坐标变化
学习目标
1. 探索关于x轴、y轴对称的点的坐标规律;
2. 探索在平面直角坐标系内平移对点的坐标的影响;
3. 理解并掌握图形变换与点的坐标变化的对应关系.
知识回顾
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
第四象限
第一象限
第二象限
第三象限
(+,+)
(-,+)
(-,-)
(+,-)
注意:坐标轴不属于任何象限.
纵坐标等于0,表示为(x,0)
横坐标等于0,表示为(0,y)
知识回顾
已知点A(-3,5)、B(-5,0)、C(-1,0)在直角坐标系中.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
C
-5
5
-5
B
(1)画出△ABC及BC边上的高AD.
(2)△ABC是等腰三角形吗?AD的长是多少?
A
D
新知探索
例 如图,点B、点C在x轴上,试在第一象限内画以BC为底,面积为10的等腰三角形ABC,并写出点A、点B、点C的坐标.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
C
-5
5
-5
B
A
解:点B、C的坐标分别为B(1,0)、C(5,0),BC= 4.
根据题意,可知等腰三角形ABC的高为5,点A在BC的垂直平分线上,
它的横坐标为3,纵坐标为5,即A(3,5). 所画△ABC如图.
讨论交流
1.把△ABC沿y轴翻折得到△A′B′C′,你能写出△A′B′C′各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
C
5
B
A
A′
C′
B′
A′ (-3,5)
B′ (-1,0)
C′ (-5,0)
讨论:翻折前后对应点的横、纵坐标有什么变化?
讨论交流
2.把△A′B′C′向下平移3个单位长度得到△A′′B′′C′′,你能写出△A′′B′′C′′各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
C
5
B
A
A′
C′
B′
A′′ (-3,2)
B′′ (-1,-3)
C′′ (-5,-3)
A′′
C′′
B′′
讨论:平移前后对应点的横、纵坐标有什么变化?
讨论交流
3.你能直接写出△ABC向上平移1个单位长度后得到的各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
5
A(3,6)
B(1,1)
C(5,1)
6
C
B
A
讨论交流
4.把△ABC沿x轴翻折得到△A1B1C1,你能写出△A1B1C1各顶点的坐标吗?
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
-5
5
6
C
B
A
A1
C1
B1
A1(3,-6)
B1(1,-1)
C1(5,-1)
讨论:翻折前后对应点的横、纵坐标有什么变化?
-6
数学实验室
O
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
(0.5,4),(0,0), (1,3),(2,3), (3,2), (3,0),(1,-1),(2,-1),(1,-3),(0,-1),(-1,-3),(-2,-1),(-1,-1),(-3,0),(-3,2),
(-2,3),(-1,3),(0,0),(0.5,4).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1.在右图的平面直角坐标系中,依次连接以下各点(最后一点不再与其他点连接),将得到一个怎样的图形
数学实验室
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(1,3)
(-1,3)
(1,-3)
(-1,-3)
2.观察图形,填空:
(1)点(1,-3)关于x轴对称的点的坐标为________,
关于y轴对称的点的坐标为__________,
关于原点对称的点的坐标为 ________.
(2)点(-1,3)关于x轴对称的点的坐标为___________,
关于y轴对称的点的坐标为_________,
关于原点对称的点的坐标为_________.
(1,3)
(-1,-3)
(-1,3)
(1,3)
(-1,-3)
(1,-3)
数学实验室
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(3,0)
(-3,0)
(3,2)
(-3,2)
(2,3)
(-2,3)
(1,3)
(-1,3)
(1,-3)
(-1,-3)
(-2,-1)
(2,-1)
(0.5,4)
(-0.5,4)
3.观察图形,讨论:
关于原点对称的点的坐标之间有什么关系?
关于y轴对称的点坐标之间有什么关系?
关于x轴对称的点坐标之间有什么关系?
新知归纳
关于坐标轴对称的点的坐标特征:
(1)关于x轴对称的两个点,横坐标相等,纵坐标互为相反数.
点P(a , b)关于x轴对称点的坐标为(a,-b)
(2)关于y轴对称的两个点,纵坐标相等,横坐标互为相反数.
点P(a , b)关于y轴对称点的坐标为(-a,b)
拓展:点P(a , b)关于原点对称点的坐标为(-a,-b)
数学实验室
4. 在图中,把线段AB先向右平移7个单位长度,再向上平移2个单位长度,得到线段 A'B'.试分别写出点 A、B、A'、B'的坐标.
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
(1)你能说出点A与点A'、点B与点B'的坐标之间的关系吗
A(-4,1)
B(-2,3)
(3,1)
(5,3)
(3,3)A′
B′(5,5)
.
.
.
.
数学实验室
4. 在图中,把线段AB先向右平移7个单位长度,再向上平移2个单位长度,得到线段 A'B'.试分别写出点 A、B、A'、B'的坐标.
O
-1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
1
x
y
1
2
3
5
-1
-2
-3
-4
-5
4
(2)如果点 C(m,n)是线段AB上的任意一点,那么当AB平移到A'B后,写出与点C对应的点C'的坐标.
A(-4,1)
B(-2,3)
(3,1)
(5,3)
(3,3)A′
B′(5,5)
.
.
.
.
(m+7, n+2)
讨论交流
2. 已知点A(a,b),B(a,c),且a≠0,b≠c,那么直线AB与坐标轴有什么位置关系?
3. 已知点C(b,d),D(c,d),且d≠0,b≠c,那么直线CD与坐标轴有什么位置关系?
1. 点的横坐标变化,纵坐标不变 , 点的位置发生了什么变化?点的纵坐标变化 ,横坐标不变呢?
新知归纳
点平移时坐标的变化规律:
(1)左右平移:纵坐标不变,横坐标左减右加;
(2)上下平移:横坐标不变,纵坐标上加下减.
与坐标轴平行的直线上的点的坐标特征:
平行于x轴的直线上的点纵坐标都相等;
平行于y轴的直线上的点横坐标都相等.
例题讲解
例 如图,图②至图④中的图形均是由图①中的图形变换得到的.
(1)请分别写出图①中点A、B、M、N的坐标;
(2)请分别写出图②至图④中与点A、B、M、N对应的点A'、B'、M'、
N'的坐标.
例题讲解
解: (1)A(2,4),B(4,0),M(1,2),N(3,2).
(2)图②中:A'(5,4),B'(7,0),M'(4,2),N'(6,2);
图③中:A'(2,-4),B'(4,0),M'(1,-2),N'(3,-2);
图④中:A'(4,8),B'(6,4),M'(3,6),N'(5,6).
1.平行于 x 轴的直线上不同的两个点的__坐标相同,__坐标不同;平行于 y 轴的直线上不同的两个点的 __坐标相同,__坐标不同.
新知巩固
2.点 P (a,b),关于 x 轴对称的点的坐标为________,关于 y 轴对称的点的坐标为________ .
3.图形左右平移,对应点的__坐标变化,__坐标不变;图形上下平移,对应点的__坐标变化,__坐标不变.
纵
横
横
纵
(a,-b)
(-a,b)
横
纵
纵
横
新知巩固
5.若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n= .
0
4. 在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是_______;
(-2,3)
6. 在平面直角坐标系中,将点P向右平移2个单位长度,再向下平移2个单位长度得点P′(-3,2),则点P的坐标为__________.
(-5,4)
7.(1)写出图①中点A、B、M、N的坐标;
新知巩固
解:(1) A(2,3),B(3,0),M(1,1.5),N(2.5,1.5);
(2)指出图①经过怎样的运动可以得到图②、图③、图④,并分别写出这 3个图中与点 A、B、M、N对应的点 A'、B'、M'、N'的坐标.
新知巩固
解:(2) 图②中:A' (4,3),B' (5,0), M'(3,1.5),N'(4.5,1.5);
新知巩固
图③中:A'(2,-3),B' (3,0), M'(1,-1.5),N'(2.5,-1.5);
图④中:A' (3,-2),B'(0,-3), M'(1.5,-1),N'(1.5,-2.5).
新知巩固
课堂小结
平面直角坐标系
关于坐标轴对称的点的坐标特征
点平移时坐标的变化规律
与坐标轴平行的直线上的点的坐标特征
当堂检测
2. 若点A(a,-1)与点B(2,b)关于y轴对称,则a-b的值是( )
A. -1 B. -3 C. 1 D. 2
1. 点A(2,-2)关于x轴对称的点的坐标为( )
A. (-2,2) B. (-2,-2) C. (2,2) D. (2,-2)
C
A
当堂检测
4. 将某图形的各顶点的横坐标保持不变,纵坐标减去3,可将该图形( )
A. 横向向右平移3个单位长度 B. 横向向左平移3个单位长度
C. 纵向向上平移3个单位长度 D. 纵向向下平移3个单位长度
3.在平面直角坐标系中,已知点A的坐标是(3,a),将点A向下平移4个单位长度得到点A′.若点A与点A′关于x轴对称,则a的值为( )
A.-2 B.2 C.-1 D.1
B
D
新知巩固
5. 四盏灯笼的位置如图.已知A、B、C、D的坐标分别是 ( 1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )
A. 将B向左平移4.5个单位
B. 将C向左平移4个单位
C. 将D向左平移5.5个单位
D. 将C向左平移3.5个单位
C
新知巩固
6.若点P(3m-12,2-m)在第三象限,且m为整数,则点P关于x轴对称的点的坐标为__________.
(-3,1)
7.在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是___________.
(-1,-2)
当堂检测
8. 已知P(a+1,b-2),Q(4,3)两点.
(1)若P,Q两点关于x轴对称,求a+b的值;
解:∵P,Q两点关于x轴对称,
∴a+1=4,b-2=-3,
∴a=3,b=-1,
∴a+b=3-1=2.
当堂检测
8. 已知P(a+1,b-2),Q(4,3)两点.
(2)若点P到y轴的距离是3,且PQ∥x轴,求点P的坐标.
解:∵点P到y轴的距离是3,
∴点P的横坐标为3或-3.
又∵PQ∥x轴,
∴点P的纵坐标为3,
∴点P的坐标为(3,3)或(-3,3).
当堂检测
9.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.已知A(1,3),A1(-2,-3),A2(4,3),A3(-8,-3),B(2,0),B1(-4,0),B2(8,0),B3(-16,0).
当堂检测
(1)观察每次变换前后的三角形有何变化,找出其中的规律,按此变化规律再将△OA3B3变换成△OA4B4,则点A4的坐标为________,点B4的坐标为________;
(16,3)
(32,0)
当堂检测
(2)若按第(1)题找到的规律将△OAB进行了n次变换,得到△OAnBn,推测点An的坐标为_________________,点Bn的坐标为_______________.
((-1)n·2n,(-1)n·3)
((-1)n·2n+1,0)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
