17.1 变量与函数
图片预览



文档简介
课件41张PPT。第17章 函数及其图象
17.1 变量与函数2.了解函数的三种表示方法.1.通过直观感知,领悟常量、变量、因变量、自变量与函数的意义.3.能应用方程思想列出实例中的等量关系,并能够列出简单问题的函数关系式.4.学会求函数自变量的取值范围,了解实际情境中函数自变量取值的限制.5.理解函数自变量与函数值的对应关系,会求指定条件下的函数值.(1)你坐过摩天轮吗?
你坐在摩天轮上时,随
着时间t的变化,你离开
地面的高度h是如何变
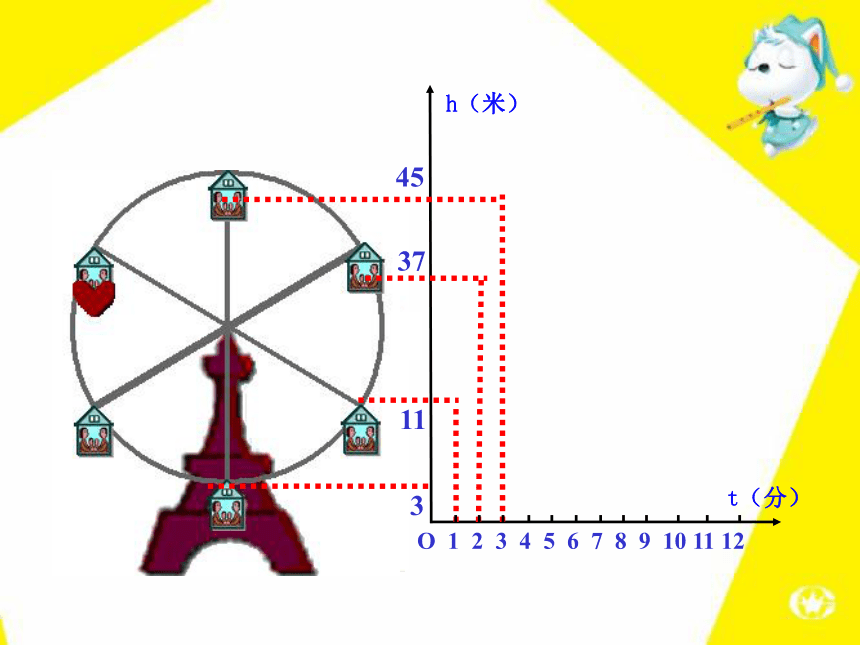
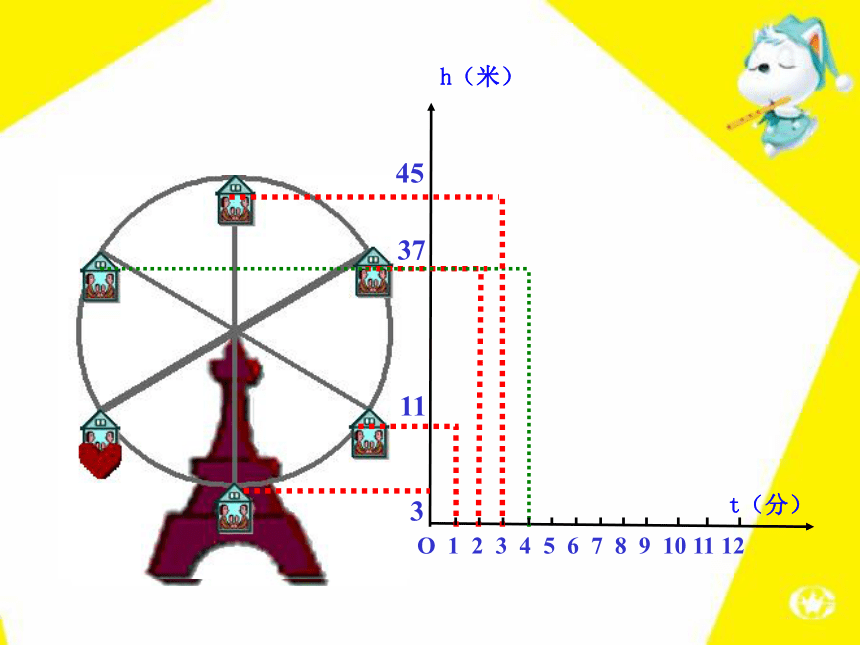
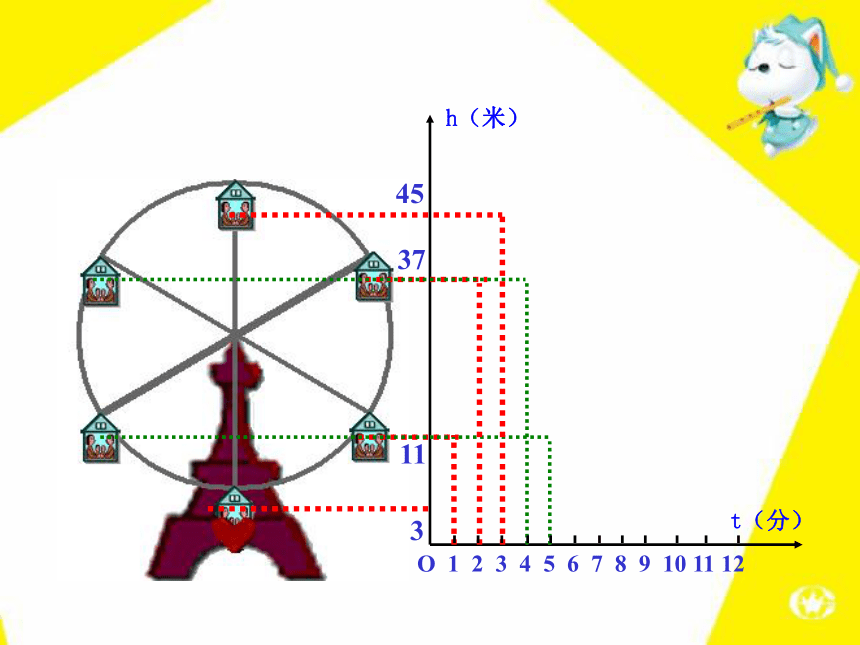
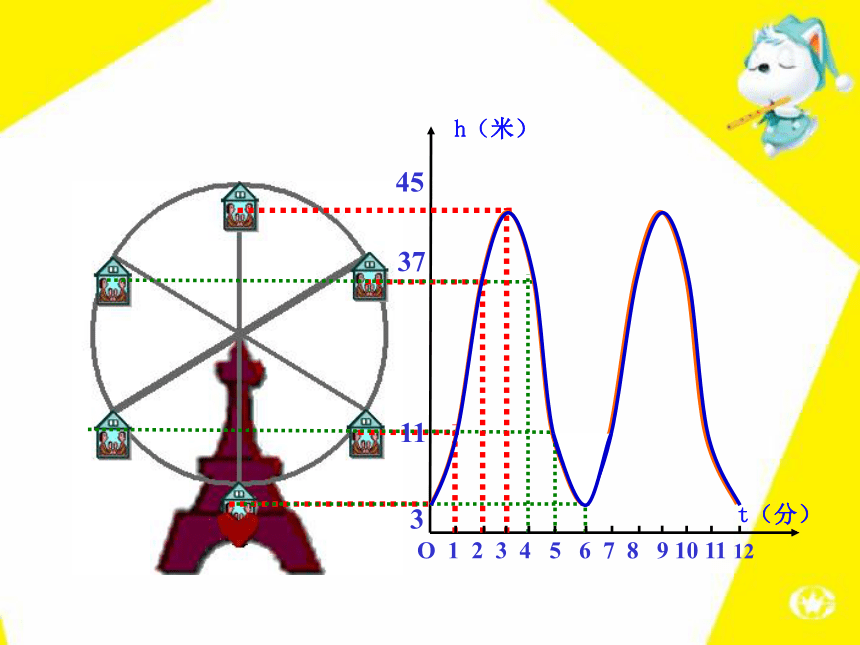
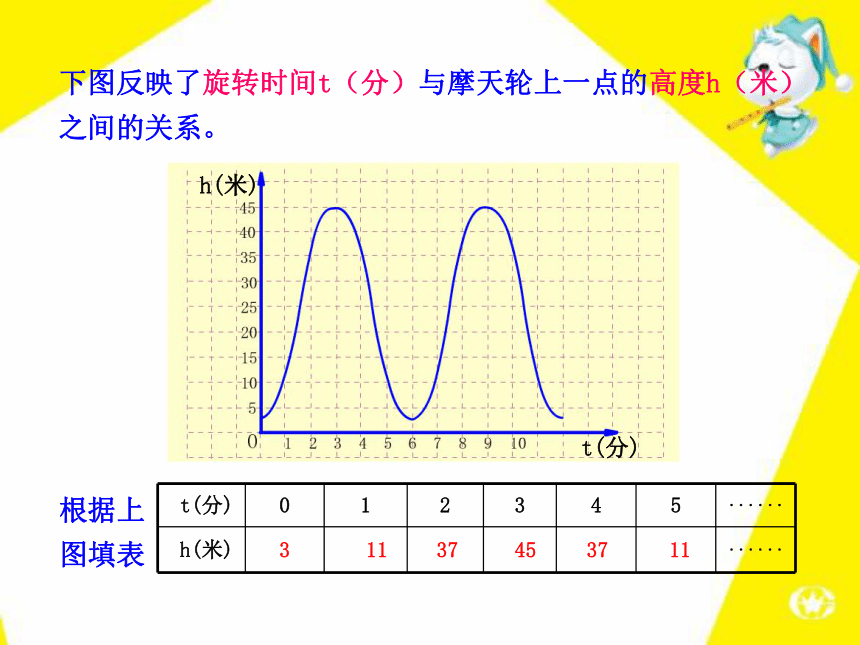
化的?O 1 2 3 4 5 6 7 8 9 10 11 123h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 12311h(米)t(分)·O 1 2 3 4 5 6 7 8 9 10 11 1231137h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)
之间的关系。31137453711根据上图填表h(米)t(分)刻画摩天轮转动过程的量是时间t和高度h,高度h随着时间t的变化而变化,它们都可以取不同的数值.像这样在某一变化过程中,可以取不同数值的量,叫做变量. 如图是某地一天内的气温变化图. 看图回答:(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温. (2)这一天中,最高气温是多少?最低气温是多少? 问题一(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低? 从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化. 在这个变化过程中存在着两个变量时间t和温度T,对于时间t每取一个值,温度T都有唯一的值与之对应.我们就说时间t是自变量,温度T是因变量.也称T是t的函数. 2013年11月中国人民银行公布的 “整存整取”年利率 观察上表,说说随着存期x的增长,相应的年利率y是如何变化的?问题二随着存期x的增长,相应的年利率y也随着增长.我们就说存期x是自变量, 年利率 y是因变量.
也称年利率y是存期x的函数.在以上变化过程中存在着两个变量:存期x和年利率y,
存期x每取一个值,年利率 y都有唯一的值与之对应. 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 观察上表回答:
(1)波长 和频率f数值之间有什么关系?
(2)波长 越大,频率f 就________. 问题三越小 在这个变化过程中存在着两个变量波长?和频率f,对于波长?每取一个值,频率f都有唯一的值与之对应.我们就说波长?是自变量,频率f是因变量. 也称频率f是波长?的函数.圆的面积随着半径的增大而增大.如果用r表示圆的半
径,S表示圆的面积,则S与r之间满足下列关系:
S= .利用这个关系式,试求出半径为1 cm,1.5 cm,
2 cm,2.6 cm,3.2 cm时圆的面积,并将结果填入下表:
(保留两位小数,?=3.1415)?r2 3.147.0712.5721.2432.17…问题四在这个变化过程中存在着两个变量:半径r和面积S,
半径r每取一个值, 面积S都有唯一的值与之对应.我们就说半径r是自变量, 面积S是因变量.也称面积
S是半径r的函数.变量:在某一变化过程中,可以取不同数值的量,叫做变量.常量:在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量.如问题三中的
300 000,问题四中的π. 上面各个问题中,都出现了两个变量,它们互相依赖,密切相关. 一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数. (1)解析法
如问题三中的f=
问题四中的S=πr2,这些表达式又称为函数关系式. 函数的表示方法(2)列表法 (3)图象法 (1)从表中你能看出该市14岁的男学生的平均身高是多少吗?
(2)该市男学生的平均身高从哪一岁开始迅速增加?
(3)上表反映了哪些变量之间的关系?其中哪个是自变量?
哪个是因变量?1.下表是某市2013年统计的该市男学生各年龄组的平均身高.【试一试】解:(1)14岁的男学生的平均身高是146.1 cm. (2)约从11岁开始身高迅速增加.(3)反映了该市男学生的平均身高和年龄两个变量之间的关系,其中年龄是自变量,平均身高是因变量.2.写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以90千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.解:(2)s=90t, S=(n-2)×180°, (1)C=2?r, 2和?是常量,r和C是变量. 90是常量,t和s是变量.2和180°是常量,n和S是变量.3.填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么? 如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式. xy4.试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式. 等腰三角形两底角相等 在上面“试一试”题3,题4中所出现的函数中,自变量的取值有限制吗?如果有,写出它的取值范围。(x取1到9之间的自然数,包括1和9) 在上面题3中,当涂黑的格子横向的加数为3时,纵向的加数是多少?当纵向的加数为6时,横向的加数是多少? y=10-x 对于题3中的函数,当自变量x=3时,对应的函数y的值y=10-3=7 ,由图知,当因变量y=6时,对应的自变量x=4. yx(泰州·中考)近期以来,大蒜和绿豆的市场价格离奇攀升,网民戏称“蒜你狠”,“豆你玩”.以绿豆为例,5月份上旬的市场价格已达16元/千克.市政府决定采取价格临时干预措施,调进绿豆以平抑市场价格.经市场调研预测,该市每调进100吨绿豆,市场价格就下降1元/千克.为了既能平抑市场价格,又要保护豆农的生产积极性,绿豆的市场价格控制在8元/千克到10元/千克之间(含8元/千克和10元/千克).问调进绿豆的吨数应在什么范围内为宜?【跟踪训练】【解析】由题意可设调进绿豆x吨,市场价格为y元,
则有16-y= ,即y=16- ,
又由绿豆的市场价格控制在8元/千克到10元/千克,
即8≤16- ≤10,解得600≤x≤800.
答:调进绿豆的吨数应在600吨到800吨之间为宜.1.若每上5个台阶就升高1米,则上升高度h(米)与上台阶数m之间的函数关系是( )
A.h=5m B.h=5+m
C.h=m-5 D.h=
【解析】选D.因每上5个台阶就升高1米,故上m个台阶上升 米,所以h= .2.(黄冈·中考)若函数 ,
则当函数值y=8时,自变量x的值是( )
A.± B.4
C.± 或4 D.4或-
【解析】选D.当x2+2=8时解得x=± ,而x≤2,
故x=- ,
当2x=8时解得x=4>2,
因此当y=8时,x=4或x=- .3.以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=v0t-4.9t2,在这个问题中,______是变量,______是常量.
【解析】此题考查常量与变量,判断的标准是看量在变化过程中是否发生变化.
答案:h,t v0,-4.94.某银行储蓄的年利率为2.25%,今存入本金10 000元,则本利和y(元)与所存年数x(年)之间的函数关系式是________.
【解析】本利和=本金+利息.
y=10 000+10 000×2.25%·x
=10 000+225x.
答案:y=10 000+225x5.当x=______时,函数y=27x+3与函数y=2x-7的函数值相同,这个函数值是______.
【解析】由于它们的函数值相同,
所以27x+3=2x-7,
25x=-10.
∴x=-
当x=- 时,y=2x-7=2×(- )-7=-
答案:- - 本节课我们学习了:意义 解析法
表示法 列表法
函数 图象法
自变量取值范围的限制条件
函数值的求法人要学会走路,也得学会摔跤,
而且只有经过摔跤才能学会走路。
——马克思
17.1 变量与函数2.了解函数的三种表示方法.1.通过直观感知,领悟常量、变量、因变量、自变量与函数的意义.3.能应用方程思想列出实例中的等量关系,并能够列出简单问题的函数关系式.4.学会求函数自变量的取值范围,了解实际情境中函数自变量取值的限制.5.理解函数自变量与函数值的对应关系,会求指定条件下的函数值.(1)你坐过摩天轮吗?
你坐在摩天轮上时,随
着时间t的变化,你离开
地面的高度h是如何变
化的?O 1 2 3 4 5 6 7 8 9 10 11 123h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 12311h(米)t(分)·O 1 2 3 4 5 6 7 8 9 10 11 1231137h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)
之间的关系。31137453711根据上图填表h(米)t(分)刻画摩天轮转动过程的量是时间t和高度h,高度h随着时间t的变化而变化,它们都可以取不同的数值.像这样在某一变化过程中,可以取不同数值的量,叫做变量. 如图是某地一天内的气温变化图. 看图回答:(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温. (2)这一天中,最高气温是多少?最低气温是多少? 问题一(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低? 从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化. 在这个变化过程中存在着两个变量时间t和温度T,对于时间t每取一个值,温度T都有唯一的值与之对应.我们就说时间t是自变量,温度T是因变量.也称T是t的函数. 2013年11月中国人民银行公布的 “整存整取”年利率 观察上表,说说随着存期x的增长,相应的年利率y是如何变化的?问题二随着存期x的增长,相应的年利率y也随着增长.我们就说存期x是自变量, 年利率 y是因变量.
也称年利率y是存期x的函数.在以上变化过程中存在着两个变量:存期x和年利率y,
存期x每取一个值,年利率 y都有唯一的值与之对应. 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 观察上表回答:
(1)波长 和频率f数值之间有什么关系?
(2)波长 越大,频率f 就________. 问题三越小 在这个变化过程中存在着两个变量波长?和频率f,对于波长?每取一个值,频率f都有唯一的值与之对应.我们就说波长?是自变量,频率f是因变量. 也称频率f是波长?的函数.圆的面积随着半径的增大而增大.如果用r表示圆的半
径,S表示圆的面积,则S与r之间满足下列关系:
S= .利用这个关系式,试求出半径为1 cm,1.5 cm,
2 cm,2.6 cm,3.2 cm时圆的面积,并将结果填入下表:
(保留两位小数,?=3.1415)?r2 3.147.0712.5721.2432.17…问题四在这个变化过程中存在着两个变量:半径r和面积S,
半径r每取一个值, 面积S都有唯一的值与之对应.我们就说半径r是自变量, 面积S是因变量.也称面积
S是半径r的函数.变量:在某一变化过程中,可以取不同数值的量,叫做变量.常量:在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量.如问题三中的
300 000,问题四中的π. 上面各个问题中,都出现了两个变量,它们互相依赖,密切相关. 一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数. (1)解析法
如问题三中的f=
问题四中的S=πr2,这些表达式又称为函数关系式. 函数的表示方法(2)列表法 (3)图象法 (1)从表中你能看出该市14岁的男学生的平均身高是多少吗?
(2)该市男学生的平均身高从哪一岁开始迅速增加?
(3)上表反映了哪些变量之间的关系?其中哪个是自变量?
哪个是因变量?1.下表是某市2013年统计的该市男学生各年龄组的平均身高.【试一试】解:(1)14岁的男学生的平均身高是146.1 cm. (2)约从11岁开始身高迅速增加.(3)反映了该市男学生的平均身高和年龄两个变量之间的关系,其中年龄是自变量,平均身高是因变量.2.写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以90千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.解:(2)s=90t, S=(n-2)×180°, (1)C=2?r, 2和?是常量,r和C是变量. 90是常量,t和s是变量.2和180°是常量,n和S是变量.3.填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么? 如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式. xy4.试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式. 等腰三角形两底角相等 在上面“试一试”题3,题4中所出现的函数中,自变量的取值有限制吗?如果有,写出它的取值范围。(x取1到9之间的自然数,包括1和9) 在上面题3中,当涂黑的格子横向的加数为3时,纵向的加数是多少?当纵向的加数为6时,横向的加数是多少? y=10-x 对于题3中的函数,当自变量x=3时,对应的函数y的值y=10-3=7 ,由图知,当因变量y=6时,对应的自变量x=4. yx(泰州·中考)近期以来,大蒜和绿豆的市场价格离奇攀升,网民戏称“蒜你狠”,“豆你玩”.以绿豆为例,5月份上旬的市场价格已达16元/千克.市政府决定采取价格临时干预措施,调进绿豆以平抑市场价格.经市场调研预测,该市每调进100吨绿豆,市场价格就下降1元/千克.为了既能平抑市场价格,又要保护豆农的生产积极性,绿豆的市场价格控制在8元/千克到10元/千克之间(含8元/千克和10元/千克).问调进绿豆的吨数应在什么范围内为宜?【跟踪训练】【解析】由题意可设调进绿豆x吨,市场价格为y元,
则有16-y= ,即y=16- ,
又由绿豆的市场价格控制在8元/千克到10元/千克,
即8≤16- ≤10,解得600≤x≤800.
答:调进绿豆的吨数应在600吨到800吨之间为宜.1.若每上5个台阶就升高1米,则上升高度h(米)与上台阶数m之间的函数关系是( )
A.h=5m B.h=5+m
C.h=m-5 D.h=
【解析】选D.因每上5个台阶就升高1米,故上m个台阶上升 米,所以h= .2.(黄冈·中考)若函数 ,
则当函数值y=8时,自变量x的值是( )
A.± B.4
C.± 或4 D.4或-
【解析】选D.当x2+2=8时解得x=± ,而x≤2,
故x=- ,
当2x=8时解得x=4>2,
因此当y=8时,x=4或x=- .3.以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=v0t-4.9t2,在这个问题中,______是变量,______是常量.
【解析】此题考查常量与变量,判断的标准是看量在变化过程中是否发生变化.
答案:h,t v0,-4.94.某银行储蓄的年利率为2.25%,今存入本金10 000元,则本利和y(元)与所存年数x(年)之间的函数关系式是________.
【解析】本利和=本金+利息.
y=10 000+10 000×2.25%·x
=10 000+225x.
答案:y=10 000+225x5.当x=______时,函数y=27x+3与函数y=2x-7的函数值相同,这个函数值是______.
【解析】由于它们的函数值相同,
所以27x+3=2x-7,
25x=-10.
∴x=-
当x=- 时,y=2x-7=2×(- )-7=-
答案:- - 本节课我们学习了:意义 解析法
表示法 列表法
函数 图象法
自变量取值范围的限制条件
函数值的求法人要学会走路,也得学会摔跤,
而且只有经过摔跤才能学会走路。
——马克思
