17.2.1 平面直角坐标系
图片预览



文档简介
课件29张PPT。17.2 函数的图象
1 平面直角坐标系2.会在坐标系内由点求坐标,由坐标找点.1.认识并能画出平面直角坐标系,理解坐标平面内点的横坐标和纵坐标的意义.3.经历画坐标系、描点、连线、看图等过程,体会数形结合思想.如何确定直线上点的位置?在直线上规定了原点、正方向、
单位长度就构成了数轴.数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.
数轴上的点和全体实数一一对应. 如果你有这张电影票,在电影院内如何找到电影票上所指的位置? 讲 台刘明张
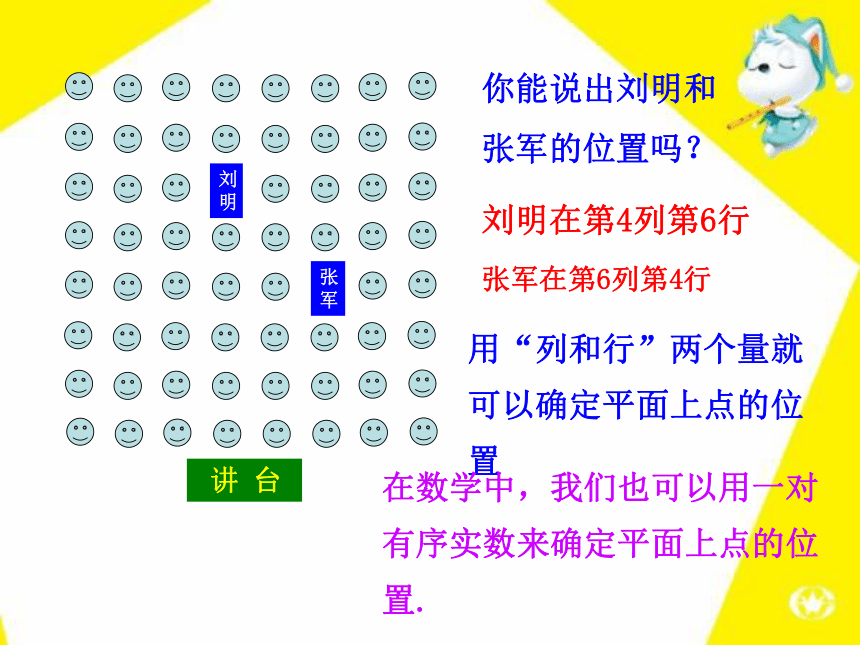
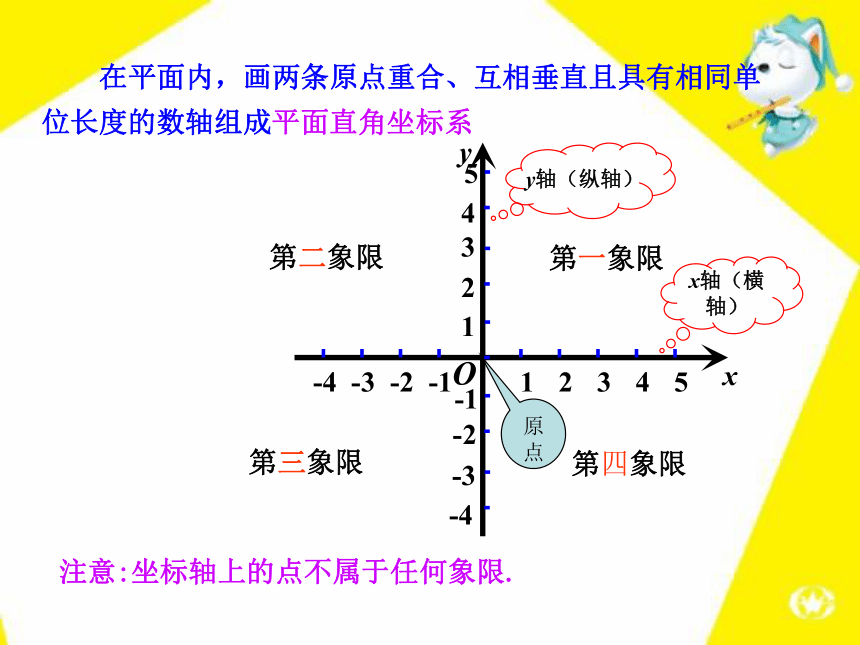
军刘明在第4列第6行张军在第6列第4行用“列和行”两个量就可以确定平面上点的位置你能说出刘明和张军的位置吗?在数学中,我们也可以用一对有序实数来确定平面上点的位置. 在平面内,画两条原点重合、互相垂直且具有相同单位长度的数轴组成平面直角坐标系y轴(纵轴)x轴(横轴)原点第一象限第二象限第三象限第四象限注意:坐标轴上的点不属于任何象限.两条数轴:(一般性特征)(1)互相垂直(其他坐标系
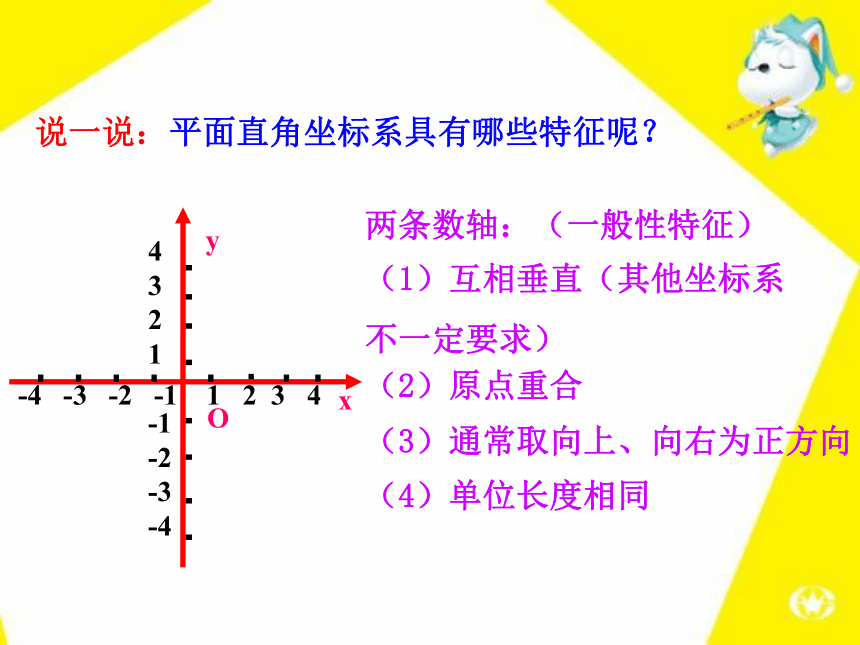
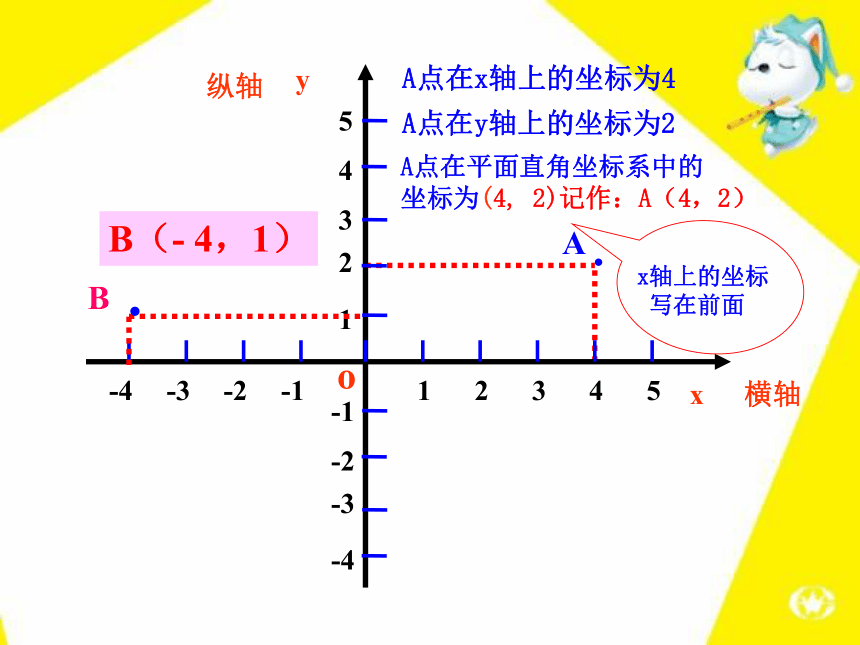
不一定要求)(2)原点重合(3)通常取向上、向右为正方向(4)单位长度相同说一说:平面直角坐标系具有哪些特征呢?-4 -3 -2 -1 1 2 3 4·AoA点在x轴上的坐标为4A点在y轴上的坐标为2A点在平面直角坐标系中的
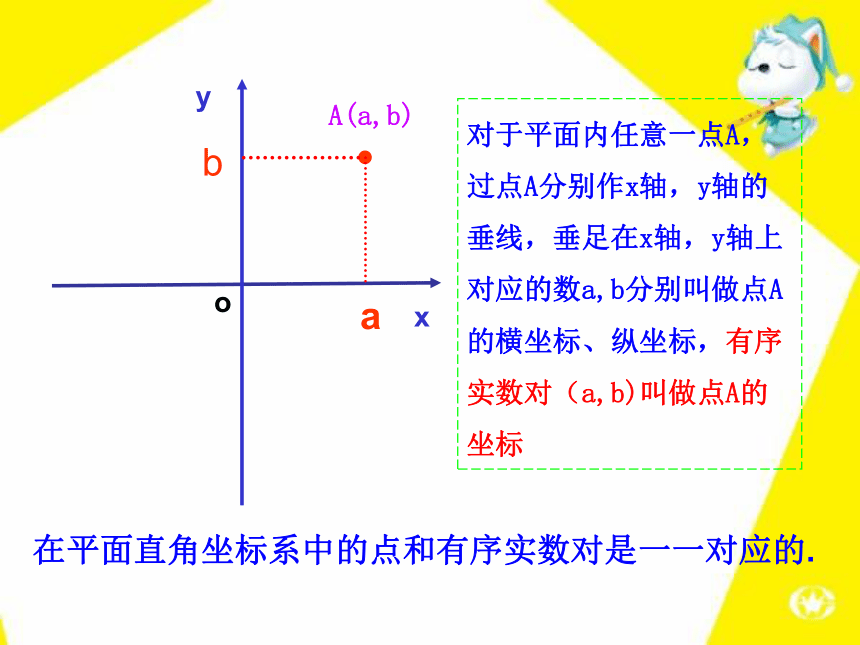
坐标为(4, 2)记作:A(4,2)B(- 4,1)oyA(a,b)ba对于平面内任意一点A,
过点A分别作x轴,y轴的
垂线,垂足在x轴,y轴上对应的数a,b分别叫做点A
的横坐标、纵坐标,有序
实数对(a,b)叫做点A的坐标x在平面直角坐标系中的点和有序实数对是一一对应的.·B·C·A·E·D( 2,3 )( 3,2 )( -2,1 )( -4,- 3 )( 1,- 2 )例1 写出图中A,B,C,D,E各点的坐标.纵轴【例题】例2 在平面直角坐标系中描出下列各点:
A(3,4)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,4)O1.描出A(3,2), B(3,-2),C(-3,2),D(-3,-2),并指出各点所在象限
2.写出图中 M,N,Q,P 的坐标A(3,2)B(3,-2)C(-3,2)D(-3,-2)··M·N····Q·P(4,4)(-4,4)(-2,0)(0,3)【跟踪训练】····1.在四个象限内的点的坐标各有什么特征?第一象限第二象限第三象限第四象限(+,+) (-,+) ( - , - ) (+, - )·····MN2.两条坐标轴上的点的坐标各有什么特征?x轴上的点纵坐标等于0,表示为(x,0)y轴上的点横坐标等于0,表示为(0,y) 第一象限第二象限第三象限第四象限(+,+) (—,+) (—,—) (+,—)(-2,0)(0,3)·QPR· T( 1 , 0 )( 4 , 0 )( 0 , -2 )( 0 , -4 )﹒·﹒(3)如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A.第四象限 B.第三象限
C.第二象限 D.第一象限D(1)已知点P( -3 , 2 ),则点P在_______象限.(2)已知点Q(0,-3),则点Q的位置在_______.第二y 轴【跟踪训练】(4)直角坐标系中有一点 M(a,b),其中ab=0 ,则点M的位置在( )
A.原点 B.x轴上
C.y轴上 D.坐标轴上 D(5)矩形ABCD中, A,B,C三点的坐标分别是(0,0), (5,0),(5,3), D点的坐标是( ).
A.(0,5) B.(5,0) C.(0,3) D.(3,0)C在直角坐标系中描出点A(3,2),分别找出它关于x轴,y轴及原点的对称点,并写出这些点的坐标.1.关于x轴对称的两点,横坐标相等,纵坐标互为相反数;2.关于y轴对称的两点,横坐标互为相反数,纵坐标相等;3.关于原点对称的两点,横坐标、纵坐标分别互为相反数.1.点A(2,-3)关于x轴对称的点坐标为_______.
关于y轴对称的点坐标为_________.
关于原点对称的点坐标为________.(2,3)(-2,-3)(-2,3)2.点(3,5)与点(3,-5)关于______轴对称.x3.点A关于原点对称点的坐标为(2,3),则点A关于
y 轴对称点的坐标为 .(2,-3)【跟踪训练】2.(遵义·中考)在一次“寻宝”
游戏中,“寻宝”人找到了如图所示
的两个标志点A(2,3)、B(4,1),
A、B两点到“宝藏”点的距离都是
则“宝藏”点的坐标是( )
(A)(1,0) (B)(5,4)
(C)(1,0)或(5,4) (D)(0,1)或(4,5)
【解析】选C.根据勾股定理,知(1,0),(5,4)到A、B两点的距离都是 ,故选C.(1)点(2,3)到x轴的距离为 ,
到y轴的距离为 .
(2)点(-2,-3)到x轴的距离为 ,
到y轴的距离为 .
(3)点(a,b)到x轴的距离为 ,
到y轴的距离为 .3232?b??a?3.填空:5.(宿迁·中考)如图,在平
面直角坐标系中,O为原点,每个
小方格的边长为1个单位长度,在
第一象限内有横、纵坐标均为整数
的A、B两点,且OA=OB=
(1)写出A、B两点的坐标;
(2)画出线段AB绕点O旋转一周所形成的图形,并求其面积(结果保留π).【解析】(1)A、B两点坐标分别
为A(3,1)、B(1,3)或
A(1,3)、B(3,1)
(2)画图(如图)
由题意得:旋转后形成一个圆环
大圆半径OA= ,
小圆半径OC=
∴S圆环=π( )2-π( )2=2π或B或A通过本课时的学习,需要我们
1.能画出平面直角坐标系,理解坐标平面内点的横坐标和纵坐标的意义,并会在坐标系内由点求坐标,由坐标找点;
2.通过归纳,得出坐标系中各个象限及坐标轴上的点的特征;
3.体会坐标平面内的点与有序实数对的一一对应关系,体会其中数形结合的意义. 成功并不能用一个人达到什么地位来衡量,而是依据他在迈向成功的过程中,到底克服了多少困难和障碍。
—— 布克?华盛顿
1 平面直角坐标系2.会在坐标系内由点求坐标,由坐标找点.1.认识并能画出平面直角坐标系,理解坐标平面内点的横坐标和纵坐标的意义.3.经历画坐标系、描点、连线、看图等过程,体会数形结合思想.如何确定直线上点的位置?在直线上规定了原点、正方向、
单位长度就构成了数轴.数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.
数轴上的点和全体实数一一对应. 如果你有这张电影票,在电影院内如何找到电影票上所指的位置? 讲 台刘明张
军刘明在第4列第6行张军在第6列第4行用“列和行”两个量就可以确定平面上点的位置你能说出刘明和张军的位置吗?在数学中,我们也可以用一对有序实数来确定平面上点的位置. 在平面内,画两条原点重合、互相垂直且具有相同单位长度的数轴组成平面直角坐标系y轴(纵轴)x轴(横轴)原点第一象限第二象限第三象限第四象限注意:坐标轴上的点不属于任何象限.两条数轴:(一般性特征)(1)互相垂直(其他坐标系
不一定要求)(2)原点重合(3)通常取向上、向右为正方向(4)单位长度相同说一说:平面直角坐标系具有哪些特征呢?-4 -3 -2 -1 1 2 3 4·AoA点在x轴上的坐标为4A点在y轴上的坐标为2A点在平面直角坐标系中的
坐标为(4, 2)记作:A(4,2)B(- 4,1)oyA(a,b)ba对于平面内任意一点A,
过点A分别作x轴,y轴的
垂线,垂足在x轴,y轴上对应的数a,b分别叫做点A
的横坐标、纵坐标,有序
实数对(a,b)叫做点A的坐标x在平面直角坐标系中的点和有序实数对是一一对应的.·B·C·A·E·D( 2,3 )( 3,2 )( -2,1 )( -4,- 3 )( 1,- 2 )例1 写出图中A,B,C,D,E各点的坐标.纵轴【例题】例2 在平面直角坐标系中描出下列各点:
A(3,4)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,4)O1.描出A(3,2), B(3,-2),C(-3,2),D(-3,-2),并指出各点所在象限
2.写出图中 M,N,Q,P 的坐标A(3,2)B(3,-2)C(-3,2)D(-3,-2)··M·N····Q·P(4,4)(-4,4)(-2,0)(0,3)【跟踪训练】····1.在四个象限内的点的坐标各有什么特征?第一象限第二象限第三象限第四象限(+,+) (-,+) ( - , - ) (+, - )·····MN2.两条坐标轴上的点的坐标各有什么特征?x轴上的点纵坐标等于0,表示为(x,0)y轴上的点横坐标等于0,表示为(0,y) 第一象限第二象限第三象限第四象限(+,+) (—,+) (—,—) (+,—)(-2,0)(0,3)·QPR· T( 1 , 0 )( 4 , 0 )( 0 , -2 )( 0 , -4 )﹒·﹒(3)如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A.第四象限 B.第三象限
C.第二象限 D.第一象限D(1)已知点P( -3 , 2 ),则点P在_______象限.(2)已知点Q(0,-3),则点Q的位置在_______.第二y 轴【跟踪训练】(4)直角坐标系中有一点 M(a,b),其中ab=0 ,则点M的位置在( )
A.原点 B.x轴上
C.y轴上 D.坐标轴上 D(5)矩形ABCD中, A,B,C三点的坐标分别是(0,0), (5,0),(5,3), D点的坐标是( ).
A.(0,5) B.(5,0) C.(0,3) D.(3,0)C在直角坐标系中描出点A(3,2),分别找出它关于x轴,y轴及原点的对称点,并写出这些点的坐标.1.关于x轴对称的两点,横坐标相等,纵坐标互为相反数;2.关于y轴对称的两点,横坐标互为相反数,纵坐标相等;3.关于原点对称的两点,横坐标、纵坐标分别互为相反数.1.点A(2,-3)关于x轴对称的点坐标为_______.
关于y轴对称的点坐标为_________.
关于原点对称的点坐标为________.(2,3)(-2,-3)(-2,3)2.点(3,5)与点(3,-5)关于______轴对称.x3.点A关于原点对称点的坐标为(2,3),则点A关于
y 轴对称点的坐标为 .(2,-3)【跟踪训练】2.(遵义·中考)在一次“寻宝”
游戏中,“寻宝”人找到了如图所示
的两个标志点A(2,3)、B(4,1),
A、B两点到“宝藏”点的距离都是
则“宝藏”点的坐标是( )
(A)(1,0) (B)(5,4)
(C)(1,0)或(5,4) (D)(0,1)或(4,5)
【解析】选C.根据勾股定理,知(1,0),(5,4)到A、B两点的距离都是 ,故选C.(1)点(2,3)到x轴的距离为 ,
到y轴的距离为 .
(2)点(-2,-3)到x轴的距离为 ,
到y轴的距离为 .
(3)点(a,b)到x轴的距离为 ,
到y轴的距离为 .3232?b??a?3.填空:5.(宿迁·中考)如图,在平
面直角坐标系中,O为原点,每个
小方格的边长为1个单位长度,在
第一象限内有横、纵坐标均为整数
的A、B两点,且OA=OB=
(1)写出A、B两点的坐标;
(2)画出线段AB绕点O旋转一周所形成的图形,并求其面积(结果保留π).【解析】(1)A、B两点坐标分别
为A(3,1)、B(1,3)或
A(1,3)、B(3,1)
(2)画图(如图)
由题意得:旋转后形成一个圆环
大圆半径OA= ,
小圆半径OC=
∴S圆环=π( )2-π( )2=2π或B或A通过本课时的学习,需要我们
1.能画出平面直角坐标系,理解坐标平面内点的横坐标和纵坐标的意义,并会在坐标系内由点求坐标,由坐标找点;
2.通过归纳,得出坐标系中各个象限及坐标轴上的点的特征;
3.体会坐标平面内的点与有序实数对的一一对应关系,体会其中数形结合的意义. 成功并不能用一个人达到什么地位来衡量,而是依据他在迈向成功的过程中,到底克服了多少困难和障碍。
—— 布克?华盛顿
