17.2.2 函数的图象课件
图片预览



文档简介
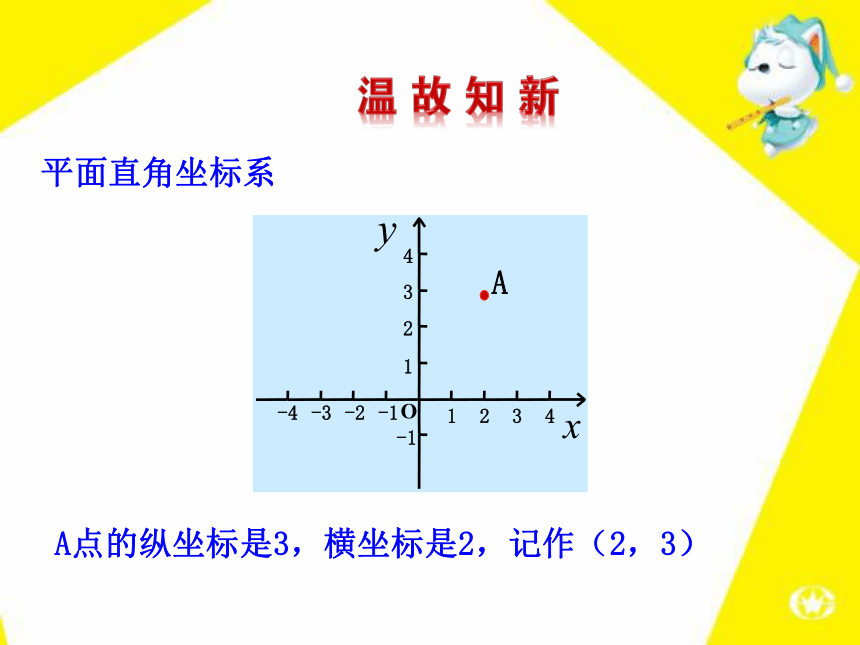
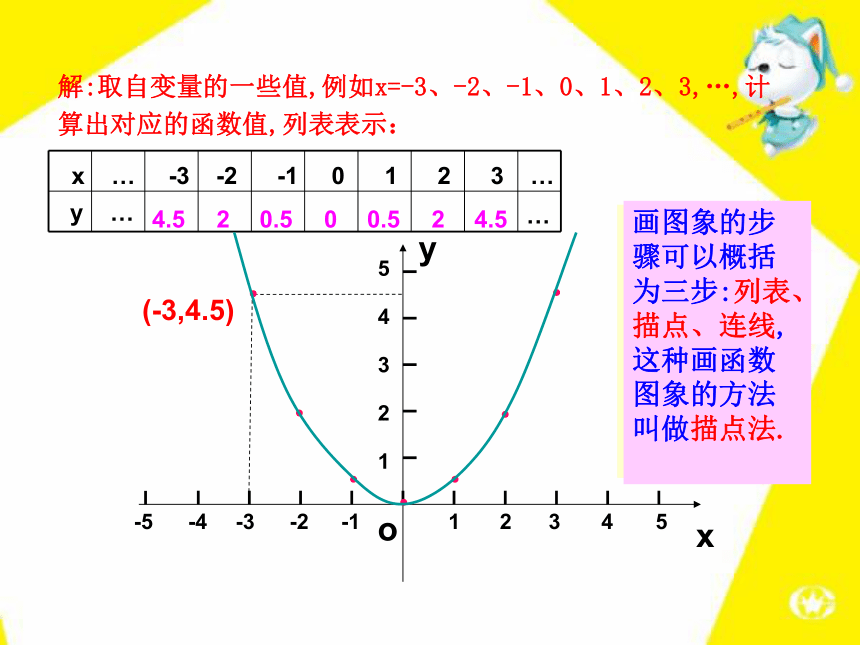
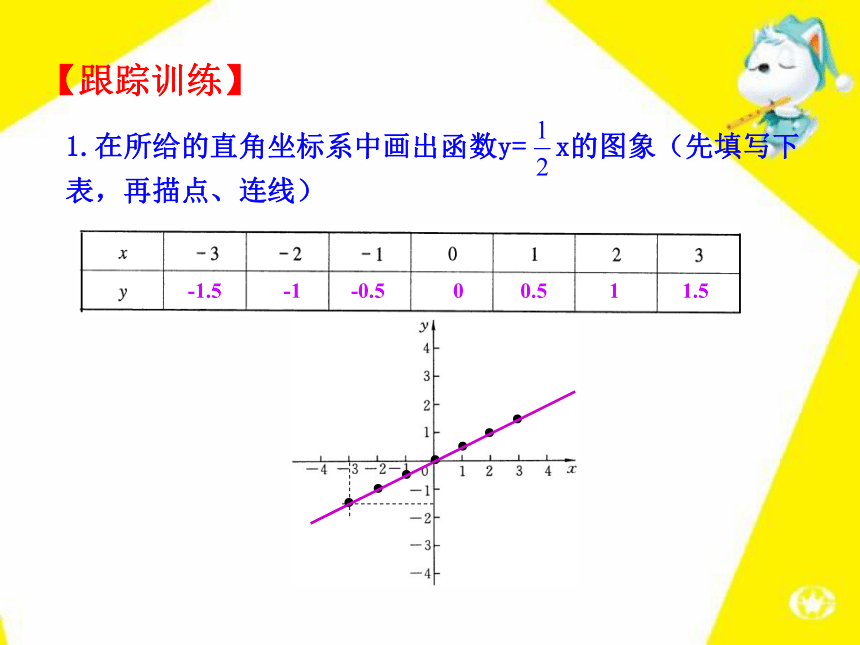
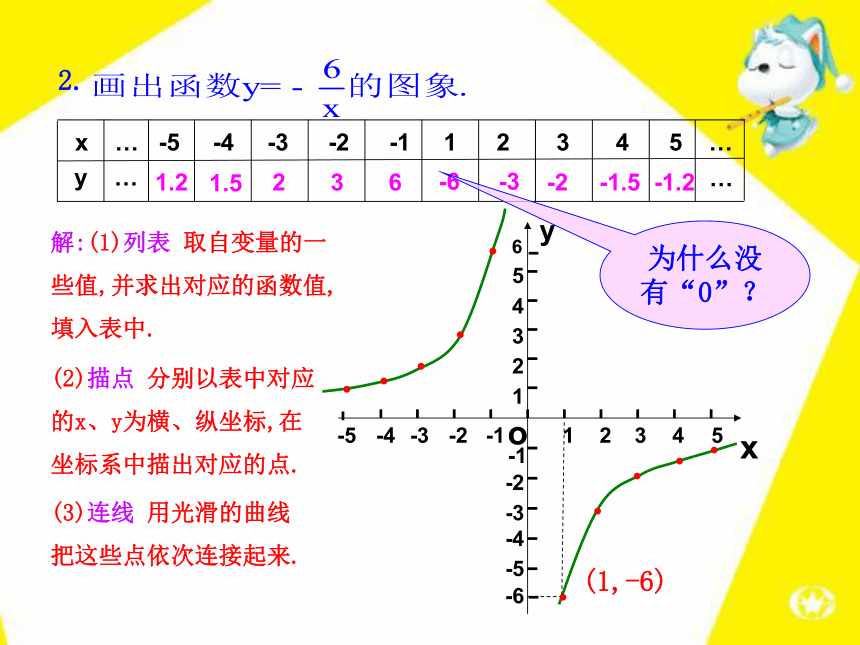
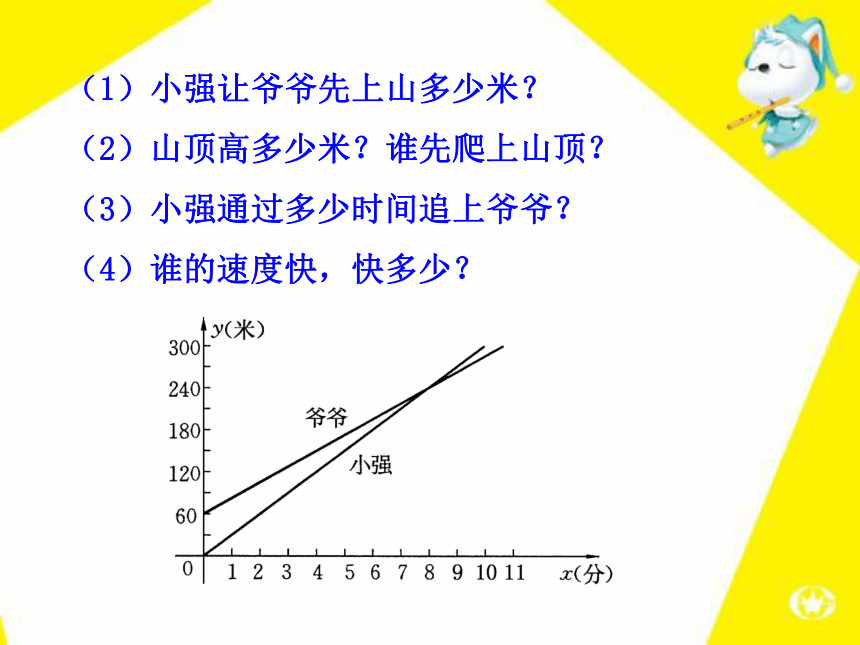
课件31张PPT。2 函数的图象2.结合问题的实际背景分析函数图象.1.掌握用描点法画简单函数的图象.3.能从图形中分析变量的相互关系,寻找对应的现实情境,预测变化趋势等问题.培养应用数学的意识.1234-1-2-3-4-11234OA平面直角坐标系A点的纵坐标是3,横坐标是2,记作(2,3)例1 画出函数 的图象.【例题】解:取自变量的一些值,例如x=-3、-2、-1、0、1、2、3,…,计算出对应的函数值,列表表示:4.520.500.524.5大家自己总结一下,看看我们在作这个函数图象的时候都经过了哪些步骤?画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法.(-3,4.5)1.在所给的直角坐标系中画出函数y= x的图象(先填写下表,再描点、连线) -1.5-1-0.500.511.5●●●●●●●【跟踪训练】y5xo-4-3-2-112345-51234-1-2-3-4-56-6解:(1)列表 取自变量的一些值,并求出对应的函数值,填入表中.(2)描点 分别以表中对应的x、y为横、纵坐标,在坐标系中描出对应的点.(3)连线 用光滑的曲线把这些点依次连接起来. -6 6-3-2-1.2-1.5 3 21.51.2(1,-6)为什么没有“0”?2.例2 王教授和孙子小强经常一起进行锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:【例题】(1)小强让爷爷先上山多少米?
(2)山顶高多少米?谁先爬上山顶?
(3)小强通过多少时间追上爷爷?
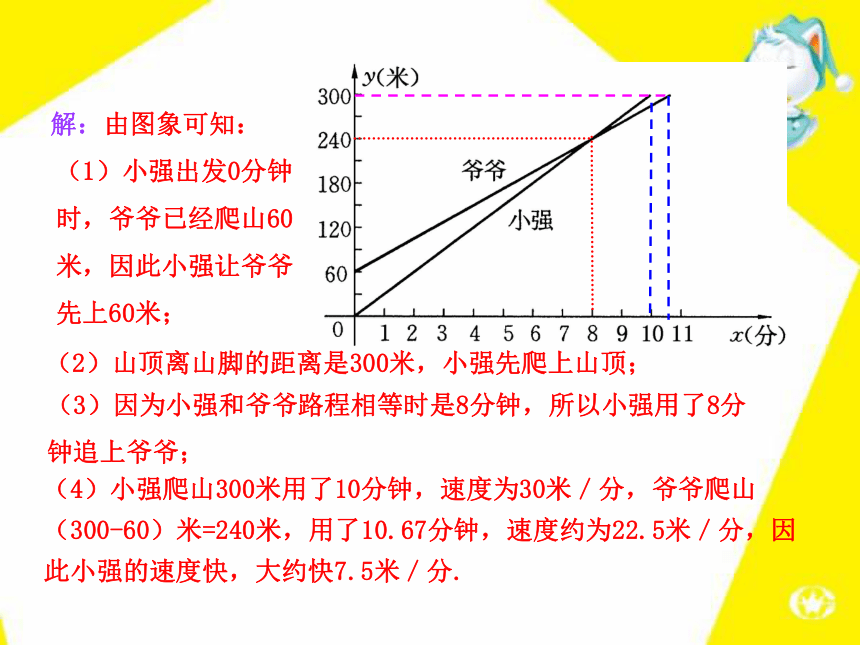
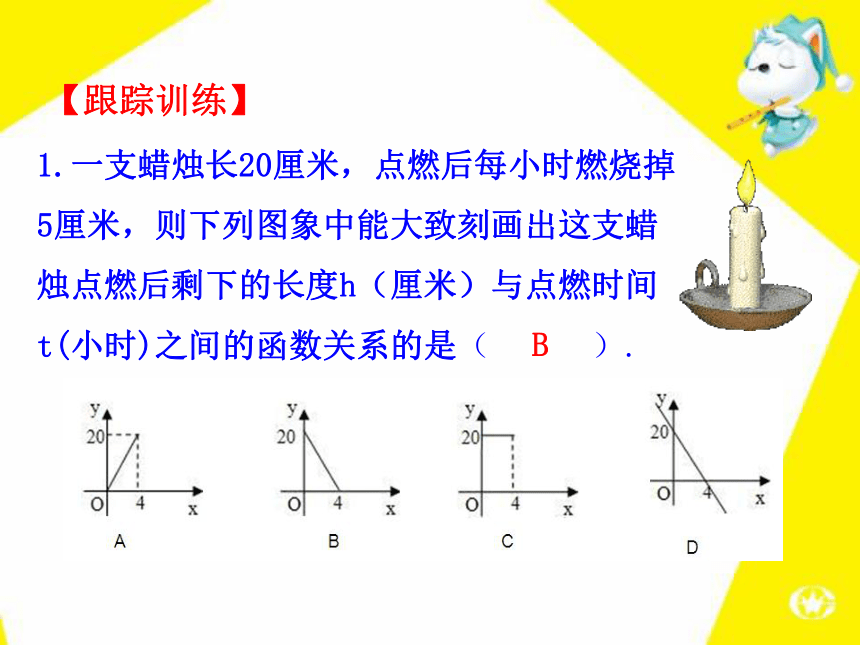
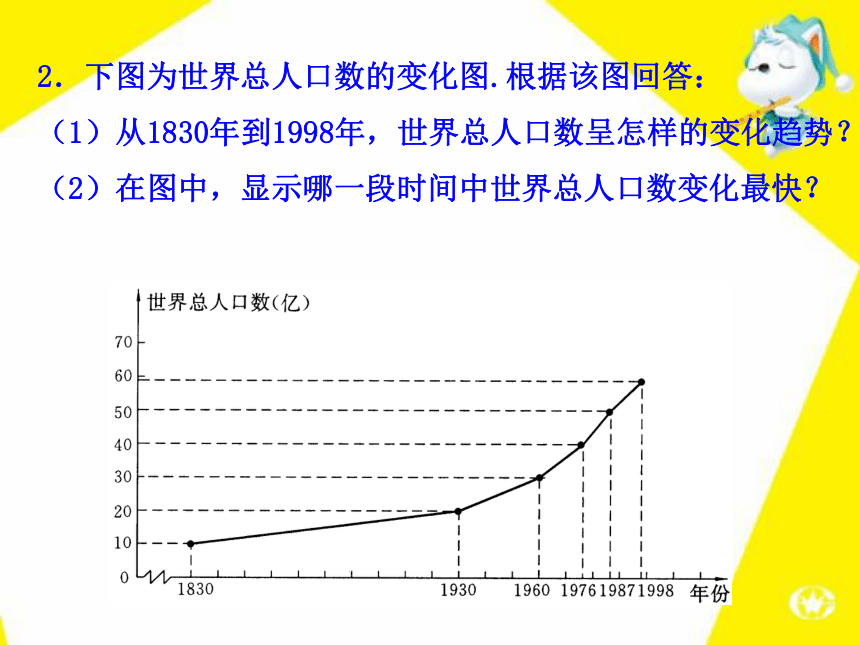
(4)谁的速度快,快多少?解:由图象可知: (1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米; (2)山顶离山脚的距离是300米,小强先爬上山顶; (3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;(4)小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.67分钟,速度约为22.5米/分,因此小强的速度快,大约快7.5米/分.1.一支蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列图象中能大致刻画出这支蜡烛点燃后剩下的长度h(厘米)与点燃时间t(小时)之间的函数关系的是( ).B【跟踪训练】2.下图为世界总人口数的变化图.根据该图回答:
(1)从1830年到1998年,世界总人口数呈怎样的变化趋势?
(2)在图中,显示哪一段时间中世界总人口数变化最快?解:(1)世界总人口数呈逐年增长的趋势,尤其自1960年开始,增长率明显加快.
(2)从1830年到1930年的100年间,世界总人口只增长10亿,1930年到1960年的30年间,世界总人口增长10亿,1960年到1976年的16年间,增长10亿,1976年到1987年的11年间,增长10亿,1987年到1998年间,增长9亿多,因此,1976年至1987年这段时间世界总人口数变化最快.3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.请你由图具体说明小明散步的情况.解:小明先走了约3分钟,到达离家250米处的一个阅报栏前看了约5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家.例3 王强在电脑上进行高尔夫球的模拟练习,在某处按函
数关系式:y= 击球,球正好进洞.其中,
y(m)是球的飞行高度,x(m)是球飞出的水平距离.
(1)试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的
起点与洞之间的距离是多少?【例题】x 0 1 2 3 4 5 6 7 8 y 0 1.4 0x(m)0-11245678-2y(m)12345-1-232.433.232.41.4(2)从图象上看,高尔夫球的最大飞行高度是_____米,
球的起点与洞之间的距离是______米.3.28解:(1)问题1:菜地离小明家多远?小明走到菜地用了多少时间?解:(1)由纵坐标看
出,菜地离小明
家1.1千米;由横
坐标看出小明走
到菜地用了15分
钟. 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.【跟踪训练】 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.问题2:小明给菜地浇水用了多少时间?(2)由横坐标看出,小明给菜地浇水用了25-15=10(分).问题3:菜地离玉米地多远?小明从菜地走到玉米地用了多少时间?(3)由纵坐标看出,菜地离玉米地2-1.1=0.9(千米); 由横坐标看出,小明从菜地到玉米地用了37-25=12(分). 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.问题4:小明给玉米地锄草用了多少时间?(4)由横坐标看出:小明给玉米地锄草用了55-37=18(分). 小明从家里出发去菜地浇水,又去玉米地锄草,然后
回家,其中x表示时间,y表示小明离他家的距离.问题5:玉米地离小明家多远?小明从玉米地走回家的平均速度是多少? (5)由纵坐标看出:玉米地离小明家2千米;由横坐标看出,小明从玉米地走回家用了80-55=25(分).平均速度是0.08 千米/分. 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.2.(济宁·中考)如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是
( )
【解析】选D.由y与x的图象可知,张老师先是离家越来越远,然后是与家的距离保持不变,最后离家越来越近回到家中,符合此情境的为D选项.3.(孝感·中考)均匀地向如图所示的一个容器注水,最后把容器注满,在注水过程中,能大致反映水面高度h随时间t变化的图象是( )【解析】选C.此容器为2个圆柱体,是规则的,即V=Sh,以恒定的速度向此容器注水,水的高度是匀速增加的.但上面圆柱的底面积小,高度增长得快且装满需要的时间短,因此选C.4.如图,乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.在这则乌鸦喝水的故事中,从乌鸦看到瓶的那刻起开始计时并设时间为x,瓶中水位的高度为y,下列图象中最符合故事情景的是( )【解析】选D.从乌鸦看到瓶子到放入第一个小石子前,其水位不变,放入石子后水位升高,乌鸦喝到水后,水位迅速下降,但比瓶中原有水位要高.通过本课时的学习,需要我们
1.知道函数图象上的点的坐标是函数的自变量与函数值的一对对应值.
2.能根据列表、描点、连线这三个步骤画出简单函数的图象.
3.通过观察函数的图象,深刻领会函数中两个变量的关系,能够从所给的图象中获取信息,从而解答一些简单的实际问题.把一页书好好地消化,胜过匆匆地阅读一本书.
(2)山顶高多少米?谁先爬上山顶?
(3)小强通过多少时间追上爷爷?
(4)谁的速度快,快多少?解:由图象可知: (1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米; (2)山顶离山脚的距离是300米,小强先爬上山顶; (3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;(4)小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.67分钟,速度约为22.5米/分,因此小强的速度快,大约快7.5米/分.1.一支蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列图象中能大致刻画出这支蜡烛点燃后剩下的长度h(厘米)与点燃时间t(小时)之间的函数关系的是( ).B【跟踪训练】2.下图为世界总人口数的变化图.根据该图回答:
(1)从1830年到1998年,世界总人口数呈怎样的变化趋势?
(2)在图中,显示哪一段时间中世界总人口数变化最快?解:(1)世界总人口数呈逐年增长的趋势,尤其自1960年开始,增长率明显加快.
(2)从1830年到1930年的100年间,世界总人口只增长10亿,1930年到1960年的30年间,世界总人口增长10亿,1960年到1976年的16年间,增长10亿,1976年到1987年的11年间,增长10亿,1987年到1998年间,增长9亿多,因此,1976年至1987年这段时间世界总人口数变化最快.3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.请你由图具体说明小明散步的情况.解:小明先走了约3分钟,到达离家250米处的一个阅报栏前看了约5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家.例3 王强在电脑上进行高尔夫球的模拟练习,在某处按函
数关系式:y= 击球,球正好进洞.其中,
y(m)是球的飞行高度,x(m)是球飞出的水平距离.
(1)试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的
起点与洞之间的距离是多少?【例题】x 0 1 2 3 4 5 6 7 8 y 0 1.4 0x(m)0-11245678-2y(m)12345-1-232.433.232.41.4(2)从图象上看,高尔夫球的最大飞行高度是_____米,
球的起点与洞之间的距离是______米.3.28解:(1)问题1:菜地离小明家多远?小明走到菜地用了多少时间?解:(1)由纵坐标看
出,菜地离小明
家1.1千米;由横
坐标看出小明走
到菜地用了15分
钟. 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.【跟踪训练】 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.问题2:小明给菜地浇水用了多少时间?(2)由横坐标看出,小明给菜地浇水用了25-15=10(分).问题3:菜地离玉米地多远?小明从菜地走到玉米地用了多少时间?(3)由纵坐标看出,菜地离玉米地2-1.1=0.9(千米); 由横坐标看出,小明从菜地到玉米地用了37-25=12(分). 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.问题4:小明给玉米地锄草用了多少时间?(4)由横坐标看出:小明给玉米地锄草用了55-37=18(分). 小明从家里出发去菜地浇水,又去玉米地锄草,然后
回家,其中x表示时间,y表示小明离他家的距离.问题5:玉米地离小明家多远?小明从玉米地走回家的平均速度是多少? (5)由纵坐标看出:玉米地离小明家2千米;由横坐标看出,小明从玉米地走回家用了80-55=25(分).平均速度是0.08 千米/分. 小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.2.(济宁·中考)如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是
( )
【解析】选D.由y与x的图象可知,张老师先是离家越来越远,然后是与家的距离保持不变,最后离家越来越近回到家中,符合此情境的为D选项.3.(孝感·中考)均匀地向如图所示的一个容器注水,最后把容器注满,在注水过程中,能大致反映水面高度h随时间t变化的图象是( )【解析】选C.此容器为2个圆柱体,是规则的,即V=Sh,以恒定的速度向此容器注水,水的高度是匀速增加的.但上面圆柱的底面积小,高度增长得快且装满需要的时间短,因此选C.4.如图,乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.在这则乌鸦喝水的故事中,从乌鸦看到瓶的那刻起开始计时并设时间为x,瓶中水位的高度为y,下列图象中最符合故事情景的是( )【解析】选D.从乌鸦看到瓶子到放入第一个小石子前,其水位不变,放入石子后水位升高,乌鸦喝到水后,水位迅速下降,但比瓶中原有水位要高.通过本课时的学习,需要我们
1.知道函数图象上的点的坐标是函数的自变量与函数值的一对对应值.
2.能根据列表、描点、连线这三个步骤画出简单函数的图象.
3.通过观察函数的图象,深刻领会函数中两个变量的关系,能够从所给的图象中获取信息,从而解答一些简单的实际问题.把一页书好好地消化,胜过匆匆地阅读一本书.
