17.3.2 一次函数的图象
图片预览



文档简介
课件24张PPT。2 一次函数的图象2.会用两点法画一次函数、正比例函数的图象.1.经历探究画一次函数图象的过程,了解一次函数、正比例函数的图象特征.3.了解直线y=kx+b(k≠0)中k、b的取值与直线的位置关系.4.能正确画出实际问题中的一次函数图象.(1)列表(2)描点(3)连线2.一次函数的概念 关系式都是自变量的一次整式.表示:y=kx+b (k,b是常数,k≠0) 注意:x的次数是1,kx+b是整式.当b=0时,一次函数y=kx(常数k≠0 )也叫做正比例函数.一次函数的图象是什么形状?1.画函数图象的一般步骤:做一做 在同一个平面直角坐标
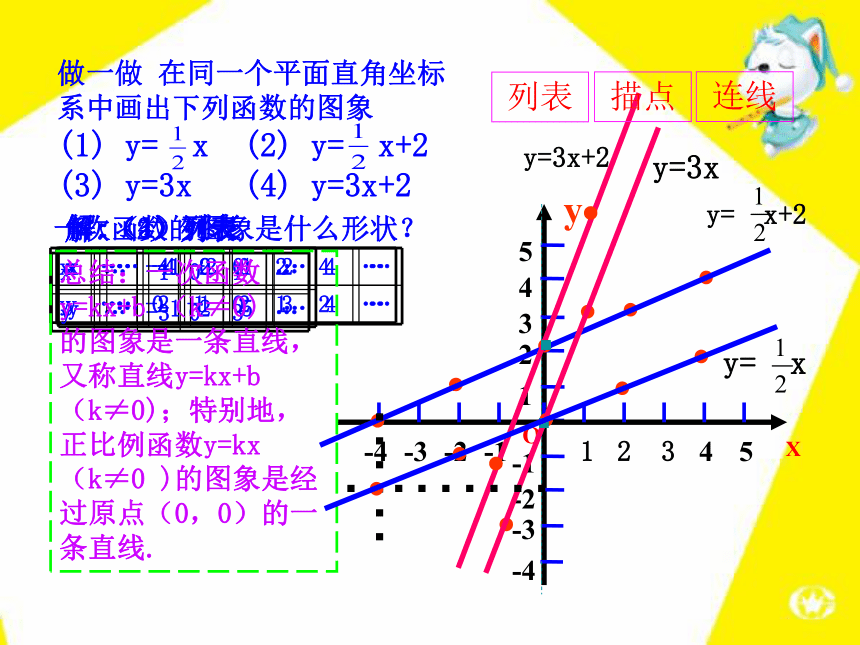
系中画出下列函数的图象
(1) y= x (2) y= x+2
(3) y=3x (4) y=3x+2解:(1)列表OX123··y=3xy=3x+2y= x y= x+2一次函数的图象是什么形状?解:(2)列表 解:(3)列表解:(4)列表……………总结:一次函数y=kx+b (k≠0)
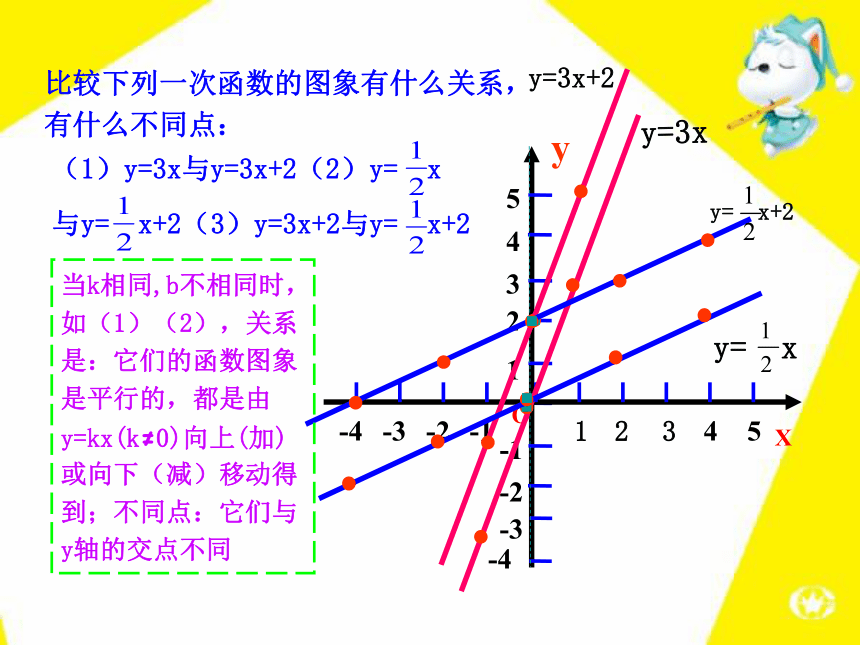
的图象是一条直线,又称直线y=kx+b (k≠0);特别地,正比例函数y=kx(k≠0 )的图象是经过原点(0,0)的一条直线.列表描点连线31425-2-4-1-3yOX123比较下列一次函数的图象有什么关系,有什么不同点:(1)y=3x与y=3x+2(2)y= x
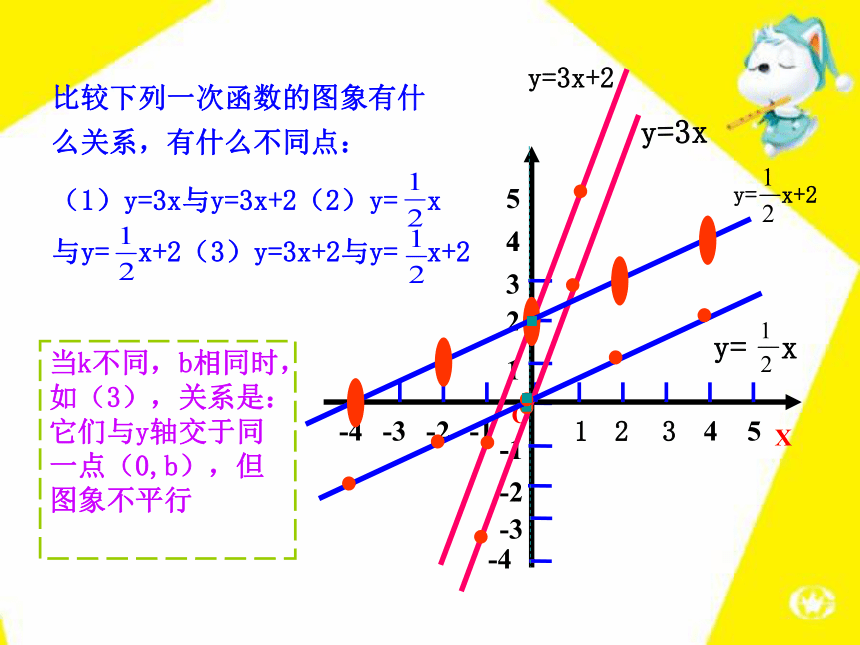
与y= x+2(3)y=3x+2与y= x+2当k相同,b不相同时,如(1)(2),关系是:它们的函数图象是平行的,都是由y=kx(k≠0)向上(加)或向下(减)移动得到;不同点:它们与y轴的交点不同3142-2-4-1-3OX123当k不同,b相同时,如(3),关系是:它们与y轴交于同一点(0,b),但图象不平行45比较下列一次函数的图象有什么关系,有什么不同点:(1)y=3x与y=3x+2(2)y= x
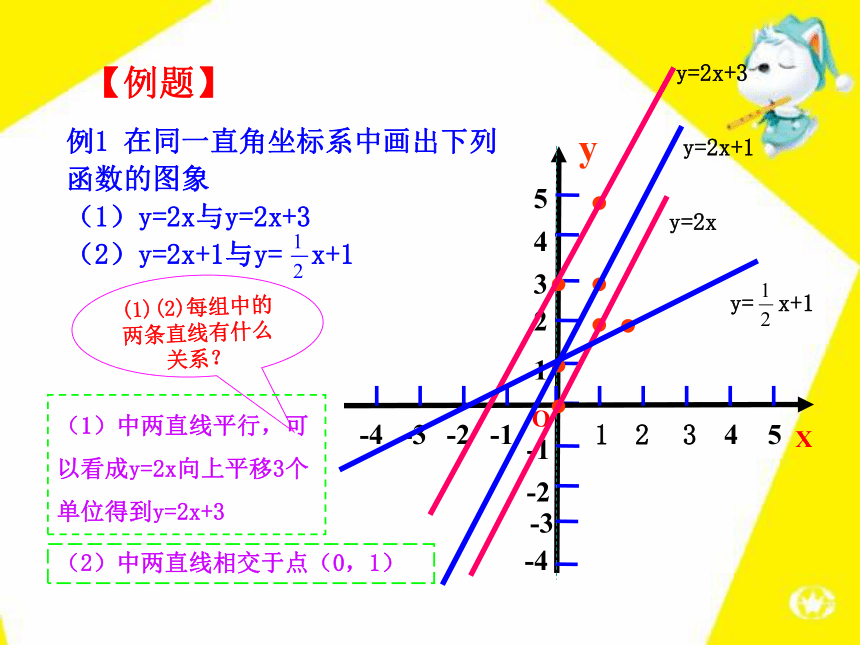
与y= x+2(3)y=3x+2与y= x+2例1 在同一直角坐标系中画出下列函数的图象
(1)y=2x与y=2x+3
(2)y=2x+1与y= x+131425-2-4-1-3yOX123y=2xy=2x+3y=2x+1y= x+1(1)(2)每组中的两条直线有什么关系?(1)中两直线平行,可以看成y=2x向上平移3个单位得到y=2x+3(2)中两直线相交于点(0,1)【例题】1.在同一直角坐标系中画出下列函
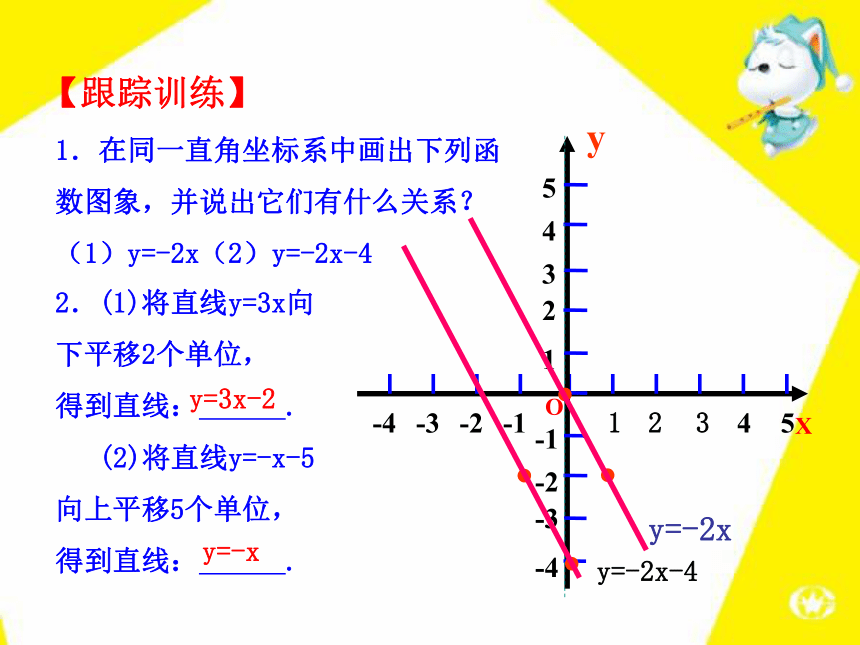
数图象,并说出它们有什么关系?
(1)y=-2x(2)y=-2x-4OX123y=-2x y=-2x-42.(1)将直线y=3x向下平移2个单位,
得到直线: .
(2)将直线y=-x-5向上平移5个单位,
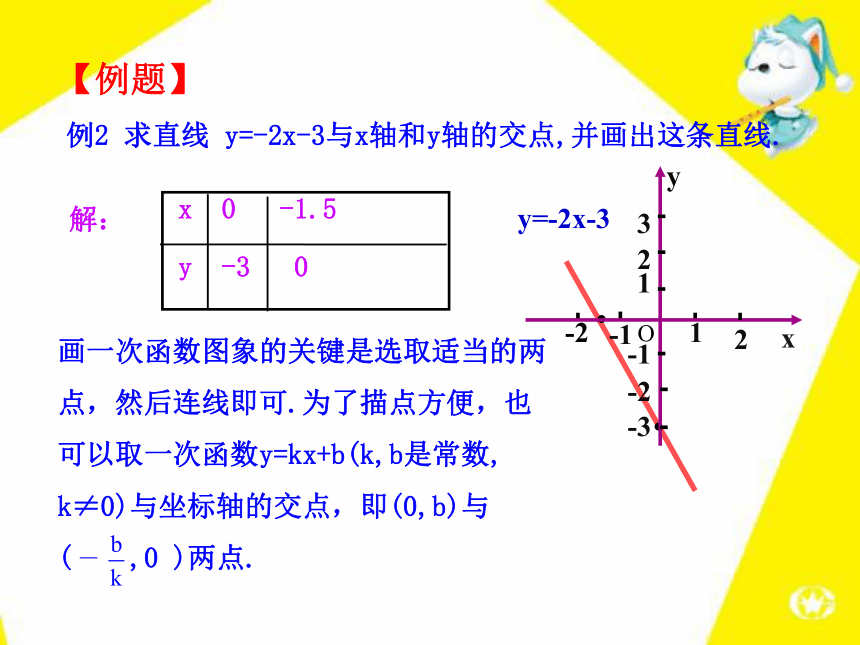
得到直线: .y=3x-2y=-x【跟踪训练】例2 求直线 y=-2x-3与x轴和y轴的交点,并画出这条直线.x 0 -1.5y -3 0y=-2x-3??-12-1-211xy23-2-3解:画一次函数图象的关键是选取适当的两点,然后连线即可.为了描点方便,也可以取一次函数y=kx+b(k,b是常数,
k≠0)与坐标轴的交点,即(0,b)与
( ,0 )两点.【例题】画出直线y=-3x的图象.解:∵当x=1时,y=-3∴图象经过(0,0)、(1,-3)两点-12-1-211xy23-2-3??y=-3x思考:直线y=-3x的图象经过哪几
个象限?直线y=-2x-3的图象呢?【跟踪训练】例3小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离. 设汽车在高速公路上行驶时间为t小时,汽车距
北京的路程为s千米,则s与t的函数关系式为
____________s=570-95t【例题】画出上述问题中小明距北京的路程s与开车时间t之间的函数s=570-95t的图象. 这里s和t取的值悬殊较大,怎么办?分析:在实际问题中,我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系并画出这个函数的图象(如图): 2.这个函数中自变量t的取值范围是什么?函数的图象是什么? 1.这个函数是不是一次函数?s=570-95t0≤t≤6, 图象是一条线段(直线的一部分)讨论是一次函数1.y=|x|中,x______y的函数,y____x 的函数(填
“是”或“不是”),图象为( )不是是 A B C D这是一个分段函数,每段都是一次函数。xy0xy0xy0xy0D【跟踪训练】2.直线y = x - 1与两坐标轴围成的三角形的面积是
多少?解: 令x=0, 得y = -1∴直线经过点(0,-1)、(2,0)令y=0, 得 x-1=0, 解得x=2∴S = × 2×1 = 11.(温州·中考)直线y=x+3与y轴的交点坐标
是( )
A.(0,3) B.(0,1)
C.(3,0) D.(1,0)
【解析】选A.当x=0时,y=3,所以交y轴于(0,3).2.(黔南州·中考)已知正比例
函数y=kx(k≠0)的图象如图所示,则
在下列选项中k值可能是( )
A.1 B.2
C.3 D.4
【解析】选B.若正比例函数y=kx经过(3,5),此时
k= ;若经过(2,6), 此时k=3,由图象可知 <k<3,
故选B.3.(上海·中考)将直线y=2x-4向上平移5个单位后,所得直线的关系式是___________.
【解析】直线y=2x-4与y轴的交点坐标为(0,-4),则向上平移5个单位后交点坐标为(0,1),则所得直线关系式为y=2x+1
答案:y=2x+14.s(km)t(h)6.Q(升)t(时) 通过本课时的学习,需要我们掌握1.一次函数图象的特点:2.一次函数图象的画法: 一次函数图象是一条直线,其中,正比例函数的图象是经过原点(0,0)的一条直线.只需要描出两个点,然
后连线即可.(0,b)志向是天才的幼苗,经过热爱劳动的双手培育,在肥田沃土里将成长为粗壮的大树.不热爱劳动,不进行自我教育,志向这棵幼苗也会连根枯死.确定个人志向,选好专业,这是幸福的源泉.
系中画出下列函数的图象
(1) y= x (2) y= x+2
(3) y=3x (4) y=3x+2解:(1)列表OX123··y=3xy=3x+2y= x y= x+2一次函数的图象是什么形状?解:(2)列表 解:(3)列表解:(4)列表……………总结:一次函数y=kx+b (k≠0)
的图象是一条直线,又称直线y=kx+b (k≠0);特别地,正比例函数y=kx(k≠0 )的图象是经过原点(0,0)的一条直线.列表描点连线31425-2-4-1-3yOX123比较下列一次函数的图象有什么关系,有什么不同点:(1)y=3x与y=3x+2(2)y= x
与y= x+2(3)y=3x+2与y= x+2当k相同,b不相同时,如(1)(2),关系是:它们的函数图象是平行的,都是由y=kx(k≠0)向上(加)或向下(减)移动得到;不同点:它们与y轴的交点不同3142-2-4-1-3OX123当k不同,b相同时,如(3),关系是:它们与y轴交于同一点(0,b),但图象不平行45比较下列一次函数的图象有什么关系,有什么不同点:(1)y=3x与y=3x+2(2)y= x
与y= x+2(3)y=3x+2与y= x+2例1 在同一直角坐标系中画出下列函数的图象
(1)y=2x与y=2x+3
(2)y=2x+1与y= x+131425-2-4-1-3yOX123y=2xy=2x+3y=2x+1y= x+1(1)(2)每组中的两条直线有什么关系?(1)中两直线平行,可以看成y=2x向上平移3个单位得到y=2x+3(2)中两直线相交于点(0,1)【例题】1.在同一直角坐标系中画出下列函
数图象,并说出它们有什么关系?
(1)y=-2x(2)y=-2x-4OX123y=-2x y=-2x-42.(1)将直线y=3x向下平移2个单位,
得到直线: .
(2)将直线y=-x-5向上平移5个单位,
得到直线: .y=3x-2y=-x【跟踪训练】例2 求直线 y=-2x-3与x轴和y轴的交点,并画出这条直线.x 0 -1.5y -3 0y=-2x-3??-12-1-211xy23-2-3解:画一次函数图象的关键是选取适当的两点,然后连线即可.为了描点方便,也可以取一次函数y=kx+b(k,b是常数,
k≠0)与坐标轴的交点,即(0,b)与
( ,0 )两点.【例题】画出直线y=-3x的图象.解:∵当x=1时,y=-3∴图象经过(0,0)、(1,-3)两点-12-1-211xy23-2-3??y=-3x思考:直线y=-3x的图象经过哪几
个象限?直线y=-2x-3的图象呢?【跟踪训练】例3小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离. 设汽车在高速公路上行驶时间为t小时,汽车距
北京的路程为s千米,则s与t的函数关系式为
____________s=570-95t【例题】画出上述问题中小明距北京的路程s与开车时间t之间的函数s=570-95t的图象. 这里s和t取的值悬殊较大,怎么办?分析:在实际问题中,我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系并画出这个函数的图象(如图): 2.这个函数中自变量t的取值范围是什么?函数的图象是什么? 1.这个函数是不是一次函数?s=570-95t0≤t≤6, 图象是一条线段(直线的一部分)讨论是一次函数1.y=|x|中,x______y的函数,y____x 的函数(填
“是”或“不是”),图象为( )不是是 A B C D这是一个分段函数,每段都是一次函数。xy0xy0xy0xy0D【跟踪训练】2.直线y = x - 1与两坐标轴围成的三角形的面积是
多少?解: 令x=0, 得y = -1∴直线经过点(0,-1)、(2,0)令y=0, 得 x-1=0, 解得x=2∴S = × 2×1 = 11.(温州·中考)直线y=x+3与y轴的交点坐标
是( )
A.(0,3) B.(0,1)
C.(3,0) D.(1,0)
【解析】选A.当x=0时,y=3,所以交y轴于(0,3).2.(黔南州·中考)已知正比例
函数y=kx(k≠0)的图象如图所示,则
在下列选项中k值可能是( )
A.1 B.2
C.3 D.4
【解析】选B.若正比例函数y=kx经过(3,5),此时
k= ;若经过(2,6), 此时k=3,由图象可知 <k<3,
故选B.3.(上海·中考)将直线y=2x-4向上平移5个单位后,所得直线的关系式是___________.
【解析】直线y=2x-4与y轴的交点坐标为(0,-4),则向上平移5个单位后交点坐标为(0,1),则所得直线关系式为y=2x+1
答案:y=2x+14.s(km)t(h)6.Q(升)t(时) 通过本课时的学习,需要我们掌握1.一次函数图象的特点:2.一次函数图象的画法: 一次函数图象是一条直线,其中,正比例函数的图象是经过原点(0,0)的一条直线.只需要描出两个点,然
后连线即可.(0,b)志向是天才的幼苗,经过热爱劳动的双手培育,在肥田沃土里将成长为粗壮的大树.不热爱劳动,不进行自我教育,志向这棵幼苗也会连根枯死.确定个人志向,选好专业,这是幸福的源泉.
