17.3.3 一次函数的性质

课件29张PPT。3 一次函数的性质2.利用一次函数的图象与性质解决相关数学问题.1.结合图象探索并理解一次函数的性质 .3.通过一次函数性质的探索与应用，进一步体会数形结合的重要性.1.作函数图象有几个步骤？2.一次函数图象有什么特点？3.作出一次函数图象需要描出几个点？列表描点连线一次函数图象是一条直线，其中，正比例函数的图象是经
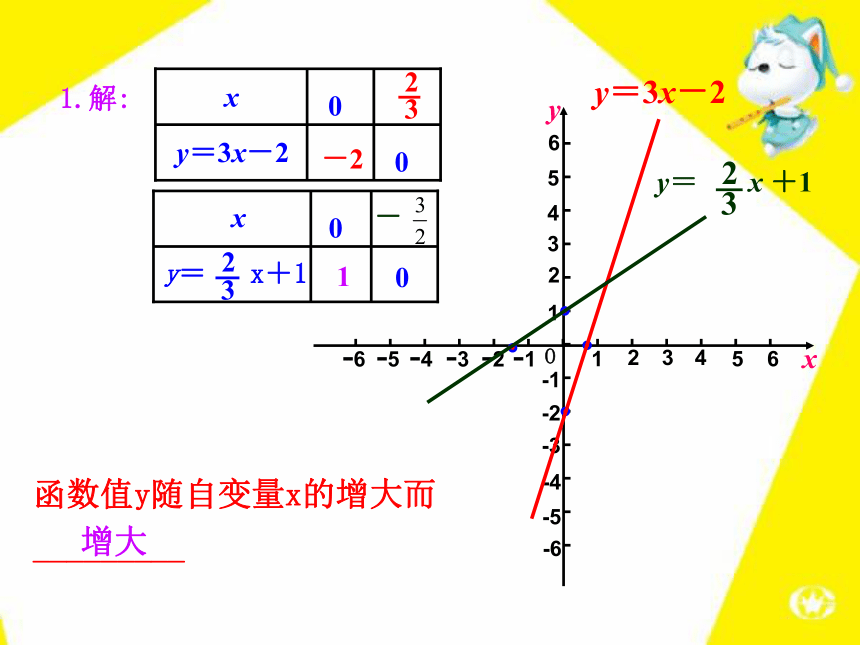
过原点（0，0）的一条直线.只需要描出两个点.(0,b)这节课我们要借助函数图象研究一次函数的性质.我们先来看下面的问题:1.在同一直角坐标系中画出下列函数的图象:y＝3x－223y＝ x＋1和2.在同一直角坐标系中画出下列函数的图象:y＝－x＋2和y＝3x－21.解:－21函数值y随自变量x的增大而
_________－增大2.解:2-12y＝－x＋2函数值y随自变量x的增大而
_________减小①确定直线y=kx+b（k≠0）经过的象限，受哪几个字母的
符号影响?②一次函数y=kx+b（k≠0）中的b究竟影响到图象的哪个
方面？常数项b决定一次函数图象与y 轴交点的位置.k、b决定直线经过的象限。-212-3-434-15y6-5-6y＝3x－2x增大y增大③k＞0时，y随x的增大而函数的图象随着x的增大从左到右增大上升12345O-1-2-3-4x6-5-6y＝－x＋2x增大y减小④k＜0时，y随x的增大而函数的图象随着x的增大从左到右减小下降xyo减小增大一、三二、四 bbbbbb常数项 决定一次函数图象与 轴交点的位置.by上升下降【归纳】1.下图中哪一个是y=x-1的大致图象？2.上图中哪一个是y=-x+2的大致图象？A B C D（ ）（ ）xy0xy0xy0xy0【跟踪训练】BC3.函数
的共同性质是（ ）
A.它们的图象都不经过第二象限
B.它们的图象都不经过原点
C.函数y都随自变量x的增大而增大
D.函数y都随自变量x的增大而减小D4.下列一次函数中，y的值随x的增大而减小的有
_____________(2)、(4)5.画出函数y=-2x+2的图象,结合图象回答下列问题：
(1)这个函数中,随着x的增大,y将增大还是减小?
它的图象从左到右怎样变化?
(2)当x取何值时,y=0?
当x取何值时,y＞0?
当0又因为y随x增大而减小，
所以2＞y＞0因为 y＞0 所以-2x+2＞0 ，x <1y=-2x+2例1 已知函数y=(m+1)x-3
(1)当m取何值时，y随x的增大而增大？这时它的图象经过哪些象限?
(2)当m取何值时，y随x的增大而减小？这时它的图象经过哪些象限?【例题】解：(1)当m+1>0，即m>-1时，y随x的增大而增大，(2)当m+1<0，即m<-1时，y随x的增大而减小，这时它的图象经过一、三、四象限；这时它的图象经过二、三、四象限.例2 已知点(2,m) 、(-3,n)都在直线
上，试比较 m和n的大小.你能想出几种判断的方法? 解：方法一 把两点的坐标代入函数关系式,当x=2时,
m= ,当x=-3时, n= ,所以m > n;方法二 因为k= >0，所以函数y随x增大而增大.
从而直接得到 m>n.1.一次函数y=kx+b中，k≠0 kb>0,且y随x的增大而减小，则它的图象大致为（ ）CA B C Dxy0xy0xy0xy0【跟踪训练】2.写出一个m的值，使相应的一次函数y = (2m－1)x+2的值随x的增大而增大.只要2m-1＞0即可.答案不唯一，如m=1等.1.一次函数y=(3m-1)x-m中，y随x的增大而减小，且函数图象不经过第一象限，则m的取值范围是( )
A.m< B.m>
C.0≤m< D.m>0
【解析】选C.由题意可得 ，解得0≤m< .2.（成都·中考）若一次函数y=kx+b(k≠0)的函数值y随x的增大而减小，且图象与y轴的负半轴相交，那么对k和b的符号判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
【解析】选D.由y=kx+b的函数值y随x的增大而减小，可得k<0,由图象与y轴的负半轴相交，可得b<0，故选D.4.函数5.(晋江·中考)已知一次函数y=kx+b的图象交y轴于正半轴，且y随x的增大而减小，请写出符合上述条件的一个关系式：_____________.
【解析】写出的函数关系式满足条件k<0，且b>0即可，答案不唯一.
答案：答案不唯一，y=-2x+36.已知y=(m-3)x- 是关于x的一次函数且y随x的增
大而增大.
（1）写出符合题意的3个m的值.
（2）设一次函数y=(m-3)x- 与x轴交于A，与y轴交
于B，m为何值时△AOB的面积等于2？【解析】(1)∵ y随x的增大而增大，
∴m-3>0,m>3,符合题意的m值只要大于3即可，答案不唯一，如4，5，6等.
（2）∵当x=0时，y=-
当y=0时，x=
∴|OA|=| |= |OB|=|- |=
由题意知， 解得m=
当m= 时，△AOB的面积等于2.通过本课时的学习，需要我们
1.掌握一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
(2)当k<0时,y随x的增大而 减小,这时函数的图象从左到右 下降.
2.能利用一次函数的性质解决相关问题.人的一生，总是难免有浮沉.不会永远如旭日东升，也不会永远痛苦潦倒.反复地一浮一沉，对于一个人来说，正是磨练.因此，浮在上面的，不必骄傲；沉在底下的，更用不着悲观.必须以率直、谦虚的态度，乐观进取的心态、向前迈进。