18.1 平行四边形的性质(第1课时)
文档属性
| 名称 | 18.1 平行四边形的性质(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-08 00:00:00 | ||
图片预览





文档简介
课件24张PPT。第18章 平行四边形
18.1 平行四边形的性质
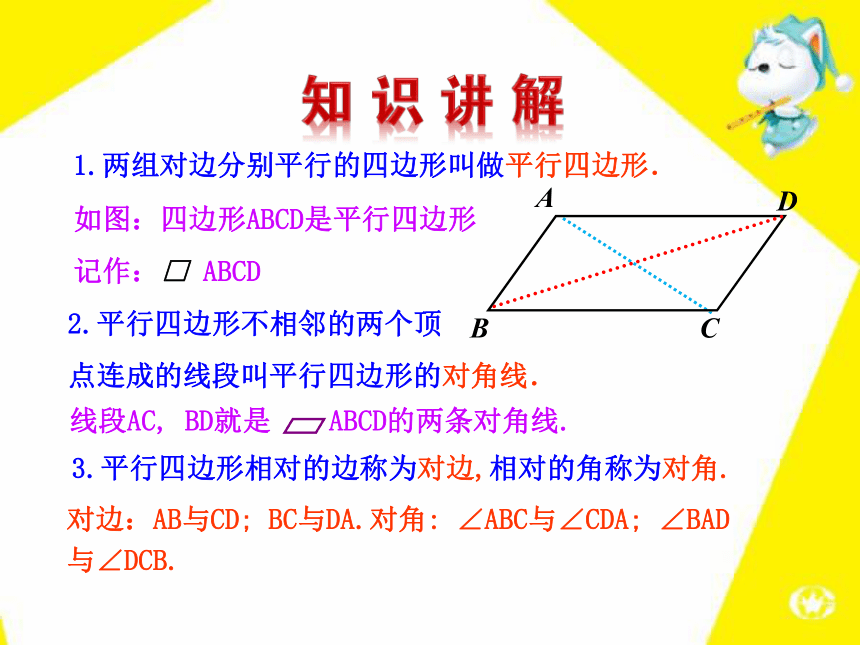
(第1课时)2、掌握平行四边形的性质,会初步运用这些性质进行有关的证明和计算 .1、理解并掌握平行四边形的定义,会用定义识别平行四边形 .3、培养学生综合运用知识的能力 .1.两组对边分别平行的四边形叫做平行四边形.如图:四边形ABCD是平行四边形记作:□ ABCD2.平行四边形不相邻的两个顶
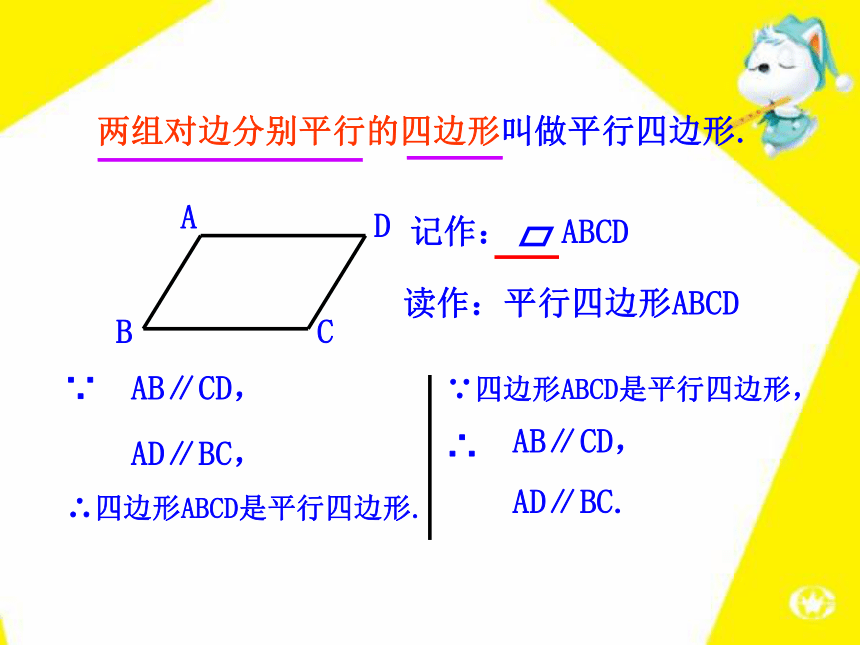
点连成的线段叫平行四边形的对角线.3.平行四边形相对的边称为对边,相对的角称为对角.对边:AB与CD; BC与DA.对角: ∠ABC与∠CDA; ∠BAD与∠DCB.两组对边分别平行的四边形叫做平行四边形.读作:平行四边形ABCD记作: ABCD∴四边形ABCD是平行四边形.∵四边形ABCD是平行四边形,AB∥CD,AD∥BC.∴ 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示? 平行四边形可以由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.【跟踪训练】平行四边形的边、角有怎样的数量关系? 请用直尺、量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确.用你以前所学的知识证明猜想.已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.即∠BAD=∠BCD.∵四边形ABCD是平行四边形, ∴AD∥BC ,AB∥CD,∴∠1=∠2,∠3=∠4.∠1=∠2,
AC=CA,
∠3=∠4,∴ △CDA ≌△ABC(ASA),∴ CD=AB, DA=BC, ∠D=∠B又∵∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3,在△CDA和 △ABC中,证明:连接AC几何语言:定理1:平行四边形的对边相等∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=BC.(平行四边形的对边相等)在 ABCD中,AB=CD,AD=BC,(平行四边形的对边相等) ∠A= ∠C, ∠B= ∠D.(平行四边形的对角相等) ∠A= ∠C, ∠B= ∠D.(平行四边形的对角相等) 定理2:平行四边形的对角相等平行四边形的性质或【例题】1.如图:在□ABCD中,根据已知你能得到哪些结论?为什么?32cm30cm56°124°124°小结:平行四边形中,知道其中一角可求出另外三个角的度数.知道其中相邻的两边可求出另外两边的长度. 【跟踪训练】2.如图是某区部分街道示意图,其中BC∥EG∥AD,
AB∥FH∥DC.图中的平行四边形共有_____个.9 从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短.
答案:一样长ABCDEGFHOA.6cm B.12cm C.4cm D.8cmABDC3.如图, □ABCD的周长是28cm,△ABC的周长是22cm,则
AC的长为( )D1.平行四边形ABCD中,∠A比∠B大20°,则∠C的度数为( )
A.60° B.80° C.100° D.120°【解析】选C.因为平行四边形邻角互补,所以∠A+∠B=180°,又因为∠A比∠B大20°,所以∠A=100°,又平行四边形对角相等,所以∠C=∠A= 100°.3.(广州·中考)已知□ABCD的周长为32,AB=4,则BC=( )
A. 4 B. 12 C. 24 D. 28【解析】选B.根据平行四边形的性质可以得出AB=CD,BC=AD,又因AB+CD+BC+AD=32,所以BC=12.4.(河北?中考)如图,在□ ABCD中,AC平分
∠DAB,AB=3,则□ ABCD的周长为( )
A.6 B.9
C.12 D.15
【解析】选C.∵四边形ABCD是平行四边形.
∴∠DAB=∠DCB,AB∥CD,AB=CD,AD∥BC,AD=BC,
又∵AC平分∠DAB,∴∠DAC=∠BAC
∴∠DAC=∠DCA,∴AD=DC.又∵AB=3,
∴□ABCD的周长为AB+BC+CD+DA=4AB=12.5.如图,在□ ABCD中, ∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
【解析】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.6.(苏州?中考)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.【解析】∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
又E是AD边上的中点,
∴AD=2AE=4,
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:12
7.(玉溪?中考)如图,
在□ ABCD中,E是AD的中点,请添加
适当条件后,构造出一对全等的三角形,并说明理由.
【解析】添加的条件是连接BE,过D作DF∥BE交BC于点F,构造的全等三角形是△ABE与△CDF.
理由:∵平行四边形ABCD中,AE=ED,
∴在△ABE与△CDF中,AB=CD,
∠EAB=∠FCD,∵ED∥BF,BE∥FD,∴四边形EDFB为平行四边形,ED=BF,又∵AD=BC,∴AE=CF,
∴△ABE≌△CDF.通过本课时的学习,需要我们掌握:
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行 对边相等
对角相等 邻角互补.
3、解决平行四边形的有关问题时,经常连接对角线将其转化为三角形问题进行解决. 一知半解的人,多不谦虚;见多识广有本领的人,一定谦虚。
—— 谢觉哉
18.1 平行四边形的性质
(第1课时)2、掌握平行四边形的性质,会初步运用这些性质进行有关的证明和计算 .1、理解并掌握平行四边形的定义,会用定义识别平行四边形 .3、培养学生综合运用知识的能力 .1.两组对边分别平行的四边形叫做平行四边形.如图:四边形ABCD是平行四边形记作:□ ABCD2.平行四边形不相邻的两个顶
点连成的线段叫平行四边形的对角线.3.平行四边形相对的边称为对边,相对的角称为对角.对边:AB与CD; BC与DA.对角: ∠ABC与∠CDA; ∠BAD与∠DCB.两组对边分别平行的四边形叫做平行四边形.读作:平行四边形ABCD记作: ABCD∴四边形ABCD是平行四边形.∵四边形ABCD是平行四边形,AB∥CD,AD∥BC.∴ 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示? 平行四边形可以由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.【跟踪训练】平行四边形的边、角有怎样的数量关系? 请用直尺、量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确.用你以前所学的知识证明猜想.已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.即∠BAD=∠BCD.∵四边形ABCD是平行四边形, ∴AD∥BC ,AB∥CD,∴∠1=∠2,∠3=∠4.∠1=∠2,
AC=CA,
∠3=∠4,∴ △CDA ≌△ABC(ASA),∴ CD=AB, DA=BC, ∠D=∠B又∵∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3,在△CDA和 △ABC中,证明:连接AC几何语言:定理1:平行四边形的对边相等∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=BC.(平行四边形的对边相等)在 ABCD中,AB=CD,AD=BC,(平行四边形的对边相等) ∠A= ∠C, ∠B= ∠D.(平行四边形的对角相等) ∠A= ∠C, ∠B= ∠D.(平行四边形的对角相等) 定理2:平行四边形的对角相等平行四边形的性质或【例题】1.如图:在□ABCD中,根据已知你能得到哪些结论?为什么?32cm30cm56°124°124°小结:平行四边形中,知道其中一角可求出另外三个角的度数.知道其中相邻的两边可求出另外两边的长度. 【跟踪训练】2.如图是某区部分街道示意图,其中BC∥EG∥AD,
AB∥FH∥DC.图中的平行四边形共有_____个.9 从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短.
答案:一样长ABCDEGFHOA.6cm B.12cm C.4cm D.8cmABDC3.如图, □ABCD的周长是28cm,△ABC的周长是22cm,则
AC的长为( )D1.平行四边形ABCD中,∠A比∠B大20°,则∠C的度数为( )
A.60° B.80° C.100° D.120°【解析】选C.因为平行四边形邻角互补,所以∠A+∠B=180°,又因为∠A比∠B大20°,所以∠A=100°,又平行四边形对角相等,所以∠C=∠A= 100°.3.(广州·中考)已知□ABCD的周长为32,AB=4,则BC=( )
A. 4 B. 12 C. 24 D. 28【解析】选B.根据平行四边形的性质可以得出AB=CD,BC=AD,又因AB+CD+BC+AD=32,所以BC=12.4.(河北?中考)如图,在□ ABCD中,AC平分
∠DAB,AB=3,则□ ABCD的周长为( )
A.6 B.9
C.12 D.15
【解析】选C.∵四边形ABCD是平行四边形.
∴∠DAB=∠DCB,AB∥CD,AB=CD,AD∥BC,AD=BC,
又∵AC平分∠DAB,∴∠DAC=∠BAC
∴∠DAC=∠DCA,∴AD=DC.又∵AB=3,
∴□ABCD的周长为AB+BC+CD+DA=4AB=12.5.如图,在□ ABCD中, ∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
【解析】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.6.(苏州?中考)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.【解析】∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
又E是AD边上的中点,
∴AD=2AE=4,
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:12
7.(玉溪?中考)如图,
在□ ABCD中,E是AD的中点,请添加
适当条件后,构造出一对全等的三角形,并说明理由.
【解析】添加的条件是连接BE,过D作DF∥BE交BC于点F,构造的全等三角形是△ABE与△CDF.
理由:∵平行四边形ABCD中,AE=ED,
∴在△ABE与△CDF中,AB=CD,
∠EAB=∠FCD,∵ED∥BF,BE∥FD,∴四边形EDFB为平行四边形,ED=BF,又∵AD=BC,∴AE=CF,
∴△ABE≌△CDF.通过本课时的学习,需要我们掌握:
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行 对边相等
对角相等 邻角互补.
3、解决平行四边形的有关问题时,经常连接对角线将其转化为三角形问题进行解决. 一知半解的人,多不谦虚;见多识广有本领的人,一定谦虚。
—— 谢觉哉
