江苏省淮安市淮安区2023-2024学年度第一学期期中学业质量调研八年级数学试卷(无答案)
文档属性
| 名称 | 江苏省淮安市淮安区2023-2024学年度第一学期期中学业质量调研八年级数学试卷(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 23:53:01 | ||
图片预览

文档简介
2023~2024学年度第一学期期中学业质量调研
八年级数学
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项填涂在答题卡上)
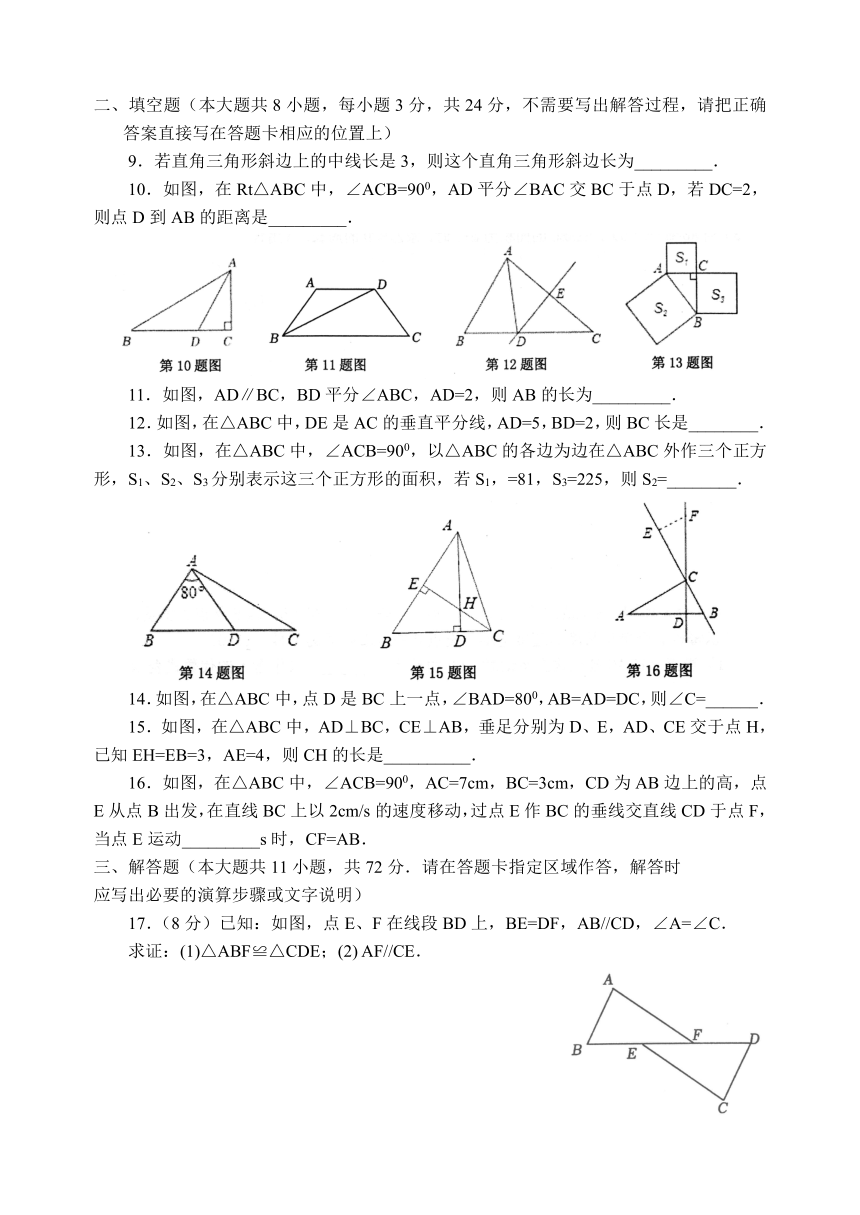
1.如图,下列甲骨文中是轴对称图形的是
2.如图,△ABC≌△DEF,若∠C=400,则∠F等于
A.500 B.300 C.900 D.400
3.如图,在△ABC和△ABD中,已知AC=AD,BC=BD,则能说明△ABC≌△ABD的依据是
A.SAS B.SSS C.AAS D.ASA
4.下列三角形各边能构成直角三角形的是
A.3、4、5 B.4、5、6 C.7、8、9 D.2、4、5
5.如图,△ABC中,AB =AC,AD⊥BC于点D,则下列结论不一定成立的是
A.∠B=∠C B.∠BAD=∠CAD C.AB=2BD D.BD=CD
6.到三角形各顶点距离相等的点是
A.三条边垂直平分线交点 B.三个内角平分线交点
C.三条中线交点 D.三条高交点
7.等腰三角形的一边等于5,一边等于12,则它的周长是
A.22 B.29 C.22或29 D.17
8.如图甲所示三角形纸片ABC中,∠B=∠C,将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙),若3AE=2AD=6,则△ABC的周长是
A. 12 B. 13
C. 14 D. 15
二、填空题(本大题共8小题,每小题3分,共24分,不需要写出解答过程,请把正确答案直接写在答题卡相应的位置上)
9.若直角三角形斜边上的中线长是3,则这个直角三角形斜边长为_________.
10.如图,在Rt△ABC中,∠ACB=900,AD平分∠BAC交BC于点D,若DC=2,则点D到AB的距离是_________.
11.如图,AD∥BC,BD平分∠ABC,AD=2,则AB的长为_________.
12.如图,在△ABC中,DE是AC的垂直平分线,AD=5,BD=2,则BC长是________.
13.如图,在△ABC中,∠ACB=900,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1,=81,S3=225,则S2=________.
14.如图,在△ABC中,点D是BC上一点,∠BAD=800,AB=AD=DC,则∠C=______.
15.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是__________.
16.如图,在△ABC中,∠ACB=900,AC=7cm,BC=3cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动_________s时,CF=AB.
三、解答题(本大题共11小题,共72分.请在答题卡指定区域作答,解答时
应写出必要的演算步骤或文字说明)
17.(8分)已知:如图,点E、F在线段BD上,BE=DF,AB//CD,∠A=∠C.
求证:(1)△ABF≌△CDE;(2) AF//CE.
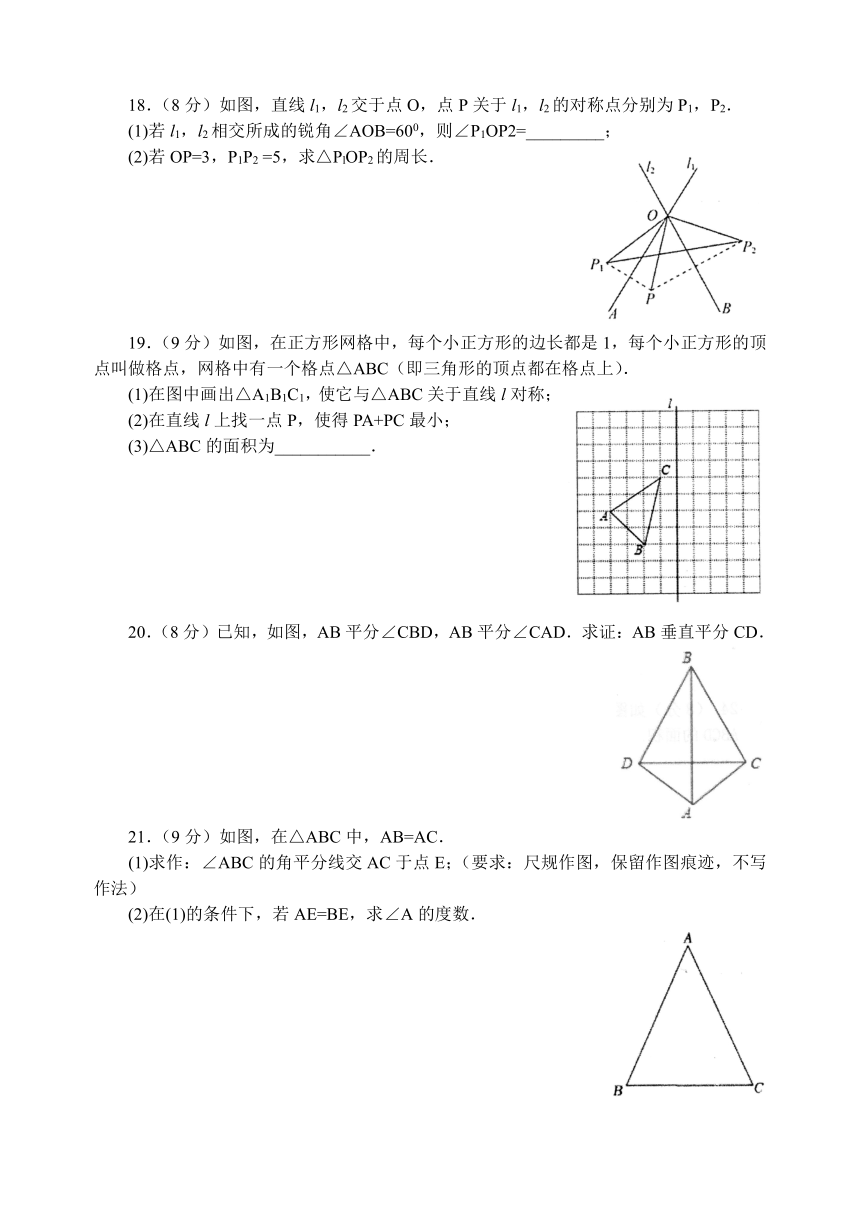
18.(8分)如图,直线l1,l2交于点O,点P关于l1,l2的对称点分别为P1,P2.
(1)若l1,l2相交所成的锐角∠AOB=600,则∠P1OP2=_________;
(2)若OP=3,P1P2 =5,求△PlOP2的周长.
19.(9分)如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△A1B1C1,使它与△ABC关于直线l对称;
(2)在直线l上找一点P,使得PA+PC最小;
(3)△ABC的面积为___________.
20.(8分)已知,如图,AB平分∠CBD,AB平分∠CAD.求证:AB垂直平分CD.
21.(9分)如图,在△ABC中,AB=AC.
(1)求作:∠ABC的角平分线交AC于点E;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AE=BE,求∠A的度数.
22.(8分)已知,如图,在△ABC中,CD⊥AB,垂足为D,BE⊥AC,垂足为E,连接DE,点G,F分别是BC,DE的中点.求证:GF⊥DE.
23.(8分)如图,E为等边△ABC的边AC上一点,且21=22,CD=BE,试判定△ADE的形状,并说明理由.
24.(8分)如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=900,计算四边形ABCD的面积.
25.(10分)如图,在△ABC中,∠C=900,把△ABC沿直线DE折叠,使△ADE与△BDE重合.
(1)若∠A=350,则∠CBD的度数为___________;
(2)若AC=6,BC=4,求AD的长;
(3)当AB=m (m>0),△ABC的面积为m+l时,求△BCD的周长.(用含m的代数式表示)
26.(14分)如图,在△ABC中,∠ACB=900,AB=13,BC=5,点P从点A出发,沿射线AC以每秒2个单位长度的速度运动.设点P的运动时间为t秒(t>0)。
(1)当点P在AC延长线上运动时,CP的长为___________;(用含t的代数式表示)
(2)若点P在∠ABC的角平分线上,求t的值;
(3)在整个运动中,直接写出△ABP是等腰三角形时t的值.
27.(12分)【知识再现】
学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称‘HL’定理)”是判定直角三角形全等的特有方法.
【简单应用】
如图(1),在△ABC中,∠BAC=900,AB=AC,点D、E分别在边AC、AB上.若CE =BD,则线段AE和线段AD的数量关系是________________.
【拓展延伸】
(1)如图(2),在△ABC中,∠BAC力钝角,AB=AC,点D、E分别在边AC、AB上.若CE=BD,则线段AE和线段AD相等吗?如果相等,请给出证明;如果不相等,请说明理由;
(2)在△ABC中,∠BAC=1200,AB=AC=m,点D在边AC上,点E在BA的延长线上,且CE=BD.则线段AE与线段AD的数量关系为__________________(用含m的式子表示).
八年级数学
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项填涂在答题卡上)
1.如图,下列甲骨文中是轴对称图形的是
2.如图,△ABC≌△DEF,若∠C=400,则∠F等于
A.500 B.300 C.900 D.400
3.如图,在△ABC和△ABD中,已知AC=AD,BC=BD,则能说明△ABC≌△ABD的依据是
A.SAS B.SSS C.AAS D.ASA
4.下列三角形各边能构成直角三角形的是
A.3、4、5 B.4、5、6 C.7、8、9 D.2、4、5
5.如图,△ABC中,AB =AC,AD⊥BC于点D,则下列结论不一定成立的是
A.∠B=∠C B.∠BAD=∠CAD C.AB=2BD D.BD=CD
6.到三角形各顶点距离相等的点是
A.三条边垂直平分线交点 B.三个内角平分线交点
C.三条中线交点 D.三条高交点
7.等腰三角形的一边等于5,一边等于12,则它的周长是
A.22 B.29 C.22或29 D.17
8.如图甲所示三角形纸片ABC中,∠B=∠C,将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙),若3AE=2AD=6,则△ABC的周长是
A. 12 B. 13
C. 14 D. 15
二、填空题(本大题共8小题,每小题3分,共24分,不需要写出解答过程,请把正确答案直接写在答题卡相应的位置上)
9.若直角三角形斜边上的中线长是3,则这个直角三角形斜边长为_________.
10.如图,在Rt△ABC中,∠ACB=900,AD平分∠BAC交BC于点D,若DC=2,则点D到AB的距离是_________.
11.如图,AD∥BC,BD平分∠ABC,AD=2,则AB的长为_________.
12.如图,在△ABC中,DE是AC的垂直平分线,AD=5,BD=2,则BC长是________.
13.如图,在△ABC中,∠ACB=900,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1,=81,S3=225,则S2=________.
14.如图,在△ABC中,点D是BC上一点,∠BAD=800,AB=AD=DC,则∠C=______.
15.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是__________.
16.如图,在△ABC中,∠ACB=900,AC=7cm,BC=3cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动_________s时,CF=AB.
三、解答题(本大题共11小题,共72分.请在答题卡指定区域作答,解答时
应写出必要的演算步骤或文字说明)
17.(8分)已知:如图,点E、F在线段BD上,BE=DF,AB//CD,∠A=∠C.
求证:(1)△ABF≌△CDE;(2) AF//CE.
18.(8分)如图,直线l1,l2交于点O,点P关于l1,l2的对称点分别为P1,P2.
(1)若l1,l2相交所成的锐角∠AOB=600,则∠P1OP2=_________;
(2)若OP=3,P1P2 =5,求△PlOP2的周长.
19.(9分)如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△A1B1C1,使它与△ABC关于直线l对称;
(2)在直线l上找一点P,使得PA+PC最小;
(3)△ABC的面积为___________.
20.(8分)已知,如图,AB平分∠CBD,AB平分∠CAD.求证:AB垂直平分CD.
21.(9分)如图,在△ABC中,AB=AC.
(1)求作:∠ABC的角平分线交AC于点E;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AE=BE,求∠A的度数.
22.(8分)已知,如图,在△ABC中,CD⊥AB,垂足为D,BE⊥AC,垂足为E,连接DE,点G,F分别是BC,DE的中点.求证:GF⊥DE.
23.(8分)如图,E为等边△ABC的边AC上一点,且21=22,CD=BE,试判定△ADE的形状,并说明理由.
24.(8分)如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=900,计算四边形ABCD的面积.
25.(10分)如图,在△ABC中,∠C=900,把△ABC沿直线DE折叠,使△ADE与△BDE重合.
(1)若∠A=350,则∠CBD的度数为___________;
(2)若AC=6,BC=4,求AD的长;
(3)当AB=m (m>0),△ABC的面积为m+l时,求△BCD的周长.(用含m的代数式表示)
26.(14分)如图,在△ABC中,∠ACB=900,AB=13,BC=5,点P从点A出发,沿射线AC以每秒2个单位长度的速度运动.设点P的运动时间为t秒(t>0)。
(1)当点P在AC延长线上运动时,CP的长为___________;(用含t的代数式表示)
(2)若点P在∠ABC的角平分线上,求t的值;
(3)在整个运动中,直接写出△ABP是等腰三角形时t的值.
27.(12分)【知识再现】
学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称‘HL’定理)”是判定直角三角形全等的特有方法.
【简单应用】
如图(1),在△ABC中,∠BAC=900,AB=AC,点D、E分别在边AC、AB上.若CE =BD,则线段AE和线段AD的数量关系是________________.
【拓展延伸】
(1)如图(2),在△ABC中,∠BAC力钝角,AB=AC,点D、E分别在边AC、AB上.若CE=BD,则线段AE和线段AD相等吗?如果相等,请给出证明;如果不相等,请说明理由;
(2)在△ABC中,∠BAC=1200,AB=AC=m,点D在边AC上,点E在BA的延长线上,且CE=BD.则线段AE与线段AD的数量关系为__________________(用含m的式子表示).
同课章节目录
