人教版九年级数学上册23.2中心对称图形(共23张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.2中心对称图形(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 804.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-08 10:34:50 | ||
图片预览





文档简介
课件23张PPT。23.2 中心对称九年级数学 要点回顾1、举例说明什么叫轴对称图形?旋转对称图形? 图15.2.4
2、下列图形是旋转对称图形吗?如果是,那么它绕至少旋转多少度后能与自身重合?阅读课本P71第二段,回答下列问题:
1、什么叫中心对称图形?什么叫对称中心?
2、中心对称图形与轴对称图形的区别?中心对称图形与旋转对称图形有什么关系?
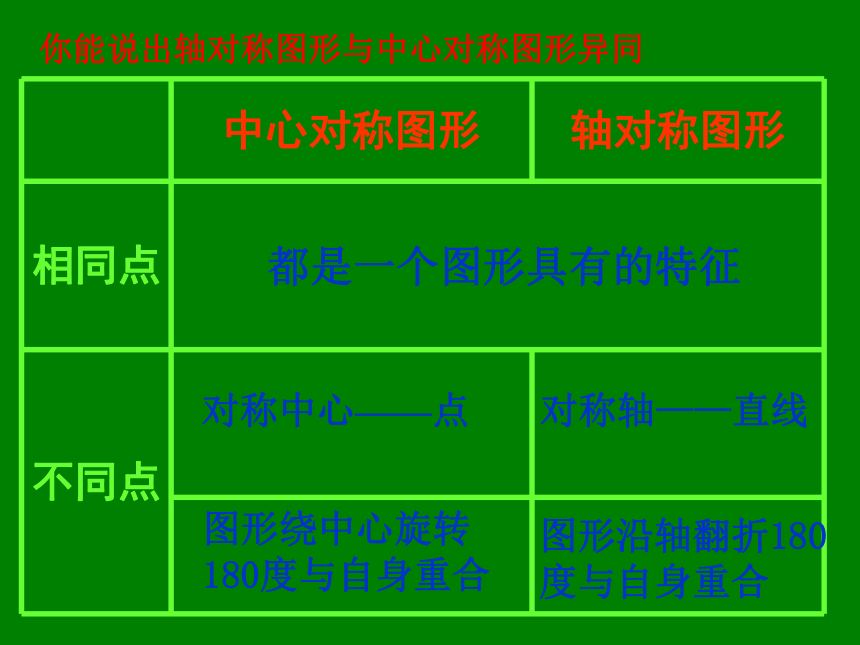
3、线段、等腰三角形、等边三角形,平行四边形、长方形、正方形、正五边形,圆是中心对称图形吗?如果是,对称中心在哪里?课题1 中心对称图形与对称中心自学指导都是一个图形具有的特征对称中心——点对称轴——直线图形绕中心旋转180度与自身重合图形沿轴翻折180度与自身重合你能说出轴对称图形与中心对称图形异同中心对称图形和旋转对称图形
的联系与区别
中心对称图形首先是旋转对称图形,
而且是特殊的旋转对称图形,
特殊在于它必须旋转180°后
才能与自身重合;
旋转对称图形有可能是
中心对称图形,是当其旋转
某一角度恰是180°与自身重合时.
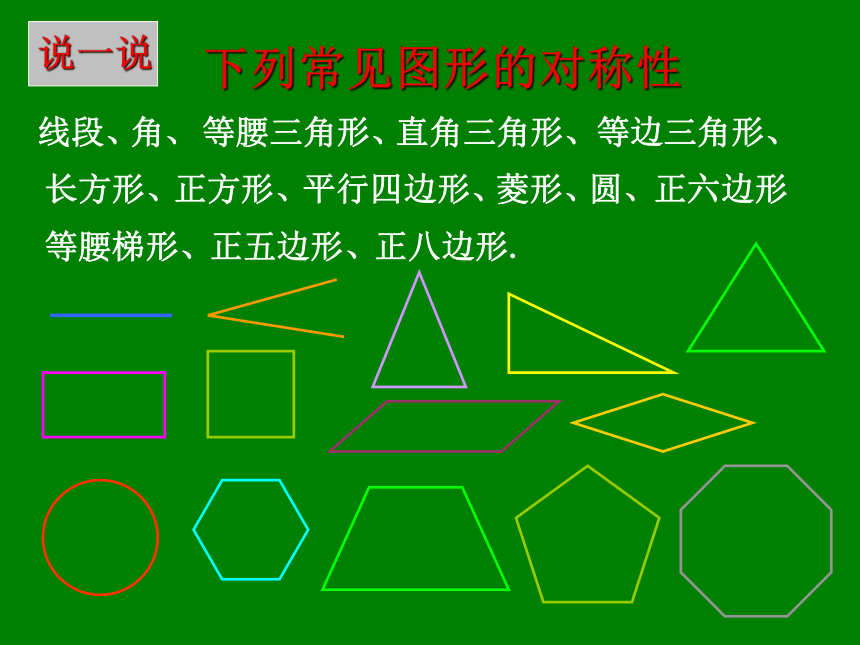
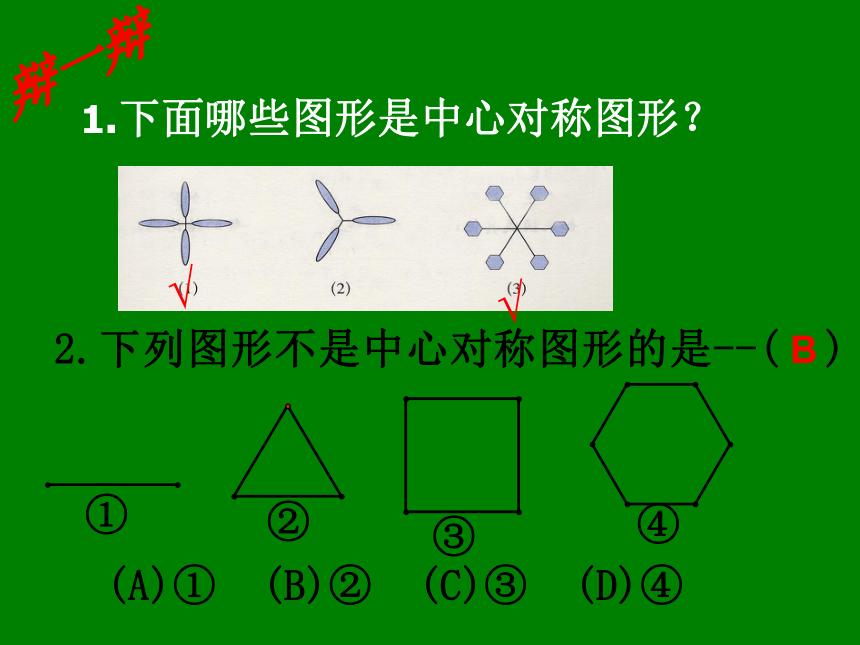
线段、下列常见图形的对称性长方形、正方形、平行四边形、等腰梯形、圆、菱形、角、等腰三角形、直角三角形、等边三角形、正六边形正五边形、正八边形.说一说1.下面哪些图形是中心对称图形?辩一辩√√BD4.除了平行四边形,你还能找到哪些多边形是 中心对称图形?
.
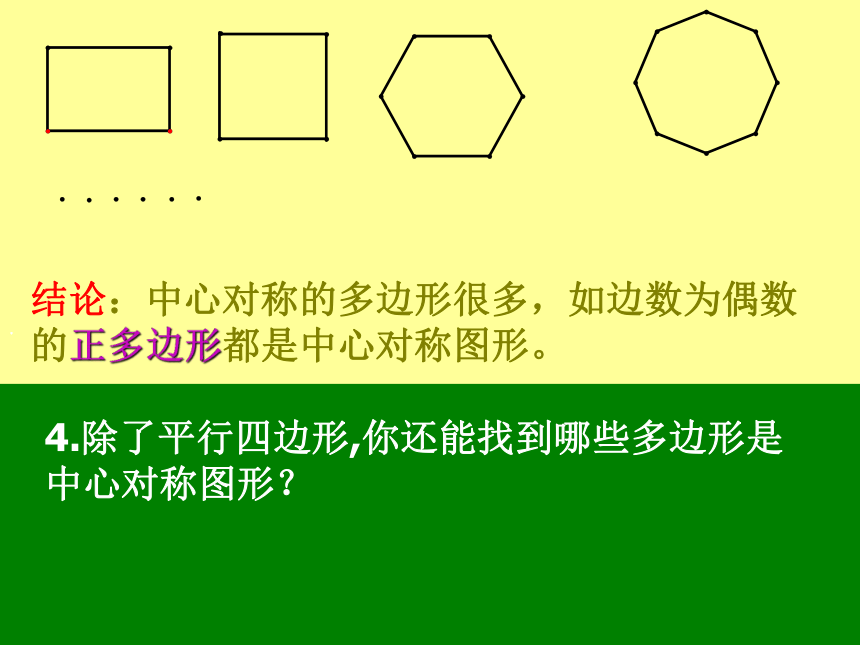
结论:中心对称的多边形很多,如边数为偶数的正多边形都是中心对称图形。阅读P71第三段,回答下列问题:
1、什么叫两个图形成中心对称? 2、什么叫对称点?
3、两个图形成中心对称与中心对称 图形有什么联系与区别?ABCDEFO 像这样把一个图形绕着某一点旋转180度, 能和 另一个图形重合,那么,我们就说这两个图形成中心对称, 这个点就叫对称中心,这两个图形中的对应点, 叫做关于中心的对称点.观察: A.O.D三点的位置关系怎样?线段AO.DO的大小关系呢?如图, △ABC与△ADE关于点A成中心对称,C、A、E三点的位置关系如何?线段AC、AE的大小关系如何?自学检测把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形成中心对称,两个图形关于点对称也称中心对称如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两
个图形看作一个整体,则成为中心对称图形。自学指导课题2 中心对称的性质与判定阅读课本P72“探索”和“归纳”,回答下列问题:
1、成中心对称的图形有什么性质?
2、如何判断两个图形关于某点成中心对称?
3、已知两个图形成中心对称,如何确定对称中心?由旋转180°知道A、O、D三点在一直线上,B、O、E且OA=OD,同理 在一直线上,且 ,C、O、F在一直线上, 且OC=OF.OB=OE个图形中, 连结即:成中心对称的两对应点的线段都经过对称中心, 且被对称中心所平分. 反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.OBECAFD自学指导课题3 画图,使之与已知图形成中心对称阅读课本P72例题,思考并总结画图的要点. 如图,已知△ABC与△A’B’C’成中心
对称,画出它们的对称中心O。解法一:根据观察,B、B’应是对应点,
连结BB’,用刻度尺找出BB’的中点O,
则点O即为所求(如图)O·解法二:根据观察,B、B’及C、C’应是
两组对应点,连结BB’、CC’相交于点O,
则点O即为所求(如图).O·例练1已知四边形ABCD关于点P成中心对称的四边形EFGH, 如图中点E是点A的对称点, 试画出四边形EFGH.P·ABCD·EFGH例练2如图,等边△ABC及其中心O,画△DEF,使△DEF和△ABC关于点O成中心对称.O·DABCEF⑴连结AO, 并延长到D,解:点D就是点A关于点O的对称点使OD=OA, ⑵同理画出点B、C关于点O的对称点⑶顺次连结DE、EF、FD则△DEF就是所求作的三角形.通过今天的学习,你有什么收获与体会?请你谈一谈1、回顾本节课的活动过程 。2、本节课学到了哪些知识? ——应用(1)中心对称图形和中心对称的定义(2)中心对称图形的性质(3)我们所学的多边形中有哪些是中心对称图形(4)中心对称图形的应用观察——分析——探索——概括? 今天你学到了什么 ? 再 见
2、下列图形是旋转对称图形吗?如果是,那么它绕至少旋转多少度后能与自身重合?阅读课本P71第二段,回答下列问题:
1、什么叫中心对称图形?什么叫对称中心?
2、中心对称图形与轴对称图形的区别?中心对称图形与旋转对称图形有什么关系?
3、线段、等腰三角形、等边三角形,平行四边形、长方形、正方形、正五边形,圆是中心对称图形吗?如果是,对称中心在哪里?课题1 中心对称图形与对称中心自学指导都是一个图形具有的特征对称中心——点对称轴——直线图形绕中心旋转180度与自身重合图形沿轴翻折180度与自身重合你能说出轴对称图形与中心对称图形异同中心对称图形和旋转对称图形
的联系与区别
中心对称图形首先是旋转对称图形,
而且是特殊的旋转对称图形,
特殊在于它必须旋转180°后
才能与自身重合;
旋转对称图形有可能是
中心对称图形,是当其旋转
某一角度恰是180°与自身重合时.
线段、下列常见图形的对称性长方形、正方形、平行四边形、等腰梯形、圆、菱形、角、等腰三角形、直角三角形、等边三角形、正六边形正五边形、正八边形.说一说1.下面哪些图形是中心对称图形?辩一辩√√BD4.除了平行四边形,你还能找到哪些多边形是 中心对称图形?
.
结论:中心对称的多边形很多,如边数为偶数的正多边形都是中心对称图形。阅读P71第三段,回答下列问题:
1、什么叫两个图形成中心对称? 2、什么叫对称点?
3、两个图形成中心对称与中心对称 图形有什么联系与区别?ABCDEFO 像这样把一个图形绕着某一点旋转180度, 能和 另一个图形重合,那么,我们就说这两个图形成中心对称, 这个点就叫对称中心,这两个图形中的对应点, 叫做关于中心的对称点.观察: A.O.D三点的位置关系怎样?线段AO.DO的大小关系呢?如图, △ABC与△ADE关于点A成中心对称,C、A、E三点的位置关系如何?线段AC、AE的大小关系如何?自学检测把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形成中心对称,两个图形关于点对称也称中心对称如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两
个图形看作一个整体,则成为中心对称图形。自学指导课题2 中心对称的性质与判定阅读课本P72“探索”和“归纳”,回答下列问题:
1、成中心对称的图形有什么性质?
2、如何判断两个图形关于某点成中心对称?
3、已知两个图形成中心对称,如何确定对称中心?由旋转180°知道A、O、D三点在一直线上,B、O、E且OA=OD,同理 在一直线上,且 ,C、O、F在一直线上, 且OC=OF.OB=OE个图形中, 连结即:成中心对称的两对应点的线段都经过对称中心, 且被对称中心所平分. 反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.OBECAFD自学指导课题3 画图,使之与已知图形成中心对称阅读课本P72例题,思考并总结画图的要点. 如图,已知△ABC与△A’B’C’成中心
对称,画出它们的对称中心O。解法一:根据观察,B、B’应是对应点,
连结BB’,用刻度尺找出BB’的中点O,
则点O即为所求(如图)O·解法二:根据观察,B、B’及C、C’应是
两组对应点,连结BB’、CC’相交于点O,
则点O即为所求(如图).O·例练1已知四边形ABCD关于点P成中心对称的四边形EFGH, 如图中点E是点A的对称点, 试画出四边形EFGH.P·ABCD·EFGH例练2如图,等边△ABC及其中心O,画△DEF,使△DEF和△ABC关于点O成中心对称.O·DABCEF⑴连结AO, 并延长到D,解:点D就是点A关于点O的对称点使OD=OA, ⑵同理画出点B、C关于点O的对称点⑶顺次连结DE、EF、FD则△DEF就是所求作的三角形.通过今天的学习,你有什么收获与体会?请你谈一谈1、回顾本节课的活动过程 。2、本节课学到了哪些知识? ——应用(1)中心对称图形和中心对称的定义(2)中心对称图形的性质(3)我们所学的多边形中有哪些是中心对称图形(4)中心对称图形的应用观察——分析——探索——概括? 今天你学到了什么 ? 再 见
同课章节目录
