广东省佛山市南海区2023-2024学年高二上学期11月期中考试数学试题(含解析)
文档属性
| 名称 | 广东省佛山市南海区2023-2024学年高二上学期11月期中考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 11:15:34 | ||
图片预览




文档简介
佛山市南海区2023-2024学年高二上学期11月期中考试数学试卷
一.选择题
1.如图,已知直线、、的斜率分别为、、,则、、的大小关系为( )
A. B. C. D.
2.在一个不透明的袋中有4个红球和个黑球,现从袋中有放回地随机摸出2个球,已知取出的球中至少有一个红球的概率为,则( )
A.1 B.2 C.3 D.4
3.如图,在空间四边形中,,,,点满足,点为的中点,则( )
A. B.
C. D.
4.已知方程表示的曲线是椭圆,则实数的取值范围是( )
A. B.
C. D.
5.若两异面直线与的方向向量分别是,,则直线与的夹角为( )
A. B. C. D.
6.在圆:内,过点的最长弦和最短弦分别是和,则四边形的面积为( )
A.24 B.12 C.10 D.8
7.抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件,“第二次向上的点数是奇数”为事件,“两次向上的点数之和能被3整除”为事件,则下列说法正确的是( )
A.事件与事件互为对立事件 B.
C. D.事件与事件相互不独立
8.已知动点在正方体的对角线(不含端点)上.设,若为钝角,则实数的取值范围为( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.设,是两个随机事件,且,,则
B.若,,,则事件与事件相互独立
C.一个人连续射击2次,事件“两次均未击中”与事件“至多一次击中”互为对立事件
D.从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是
10.已知椭圆:的左、右焦点分别为,,点在上,且的最大值为3,最小值为1,则( )
A.椭圆的圆心率为
B.的周长为4
C.若,则的面积为
D.若,则
11.已知经过点的圆的圆心坐标为(为整数),且与直线:相切,直线:与圆相交于、两点,下列说法正确的是( )
A.圆的标准方程为
B.若,则实数的值为
C.若,则直线的方程为或
D.弦的中点的轨迹方程为
12.如图,正方体中,为的中点,为棱上的动点,则下列结论正确的是( )
A.存在点,使平面
B.存在点,使
C.四面体的体积为定值
D.二面角的余弦值取值范围是
三、填空题
13.已知直线经过椭圆的一个焦点和一个顶点,则此椭圆的离心率______.
14.已知点,直线过原点,且平行于向量,则点到直线的距离是______.
15.已知事件,相互独立,且,,则______.
16.已知,,若直线上存在点,使得,则的取值范围是______.
四.解答题
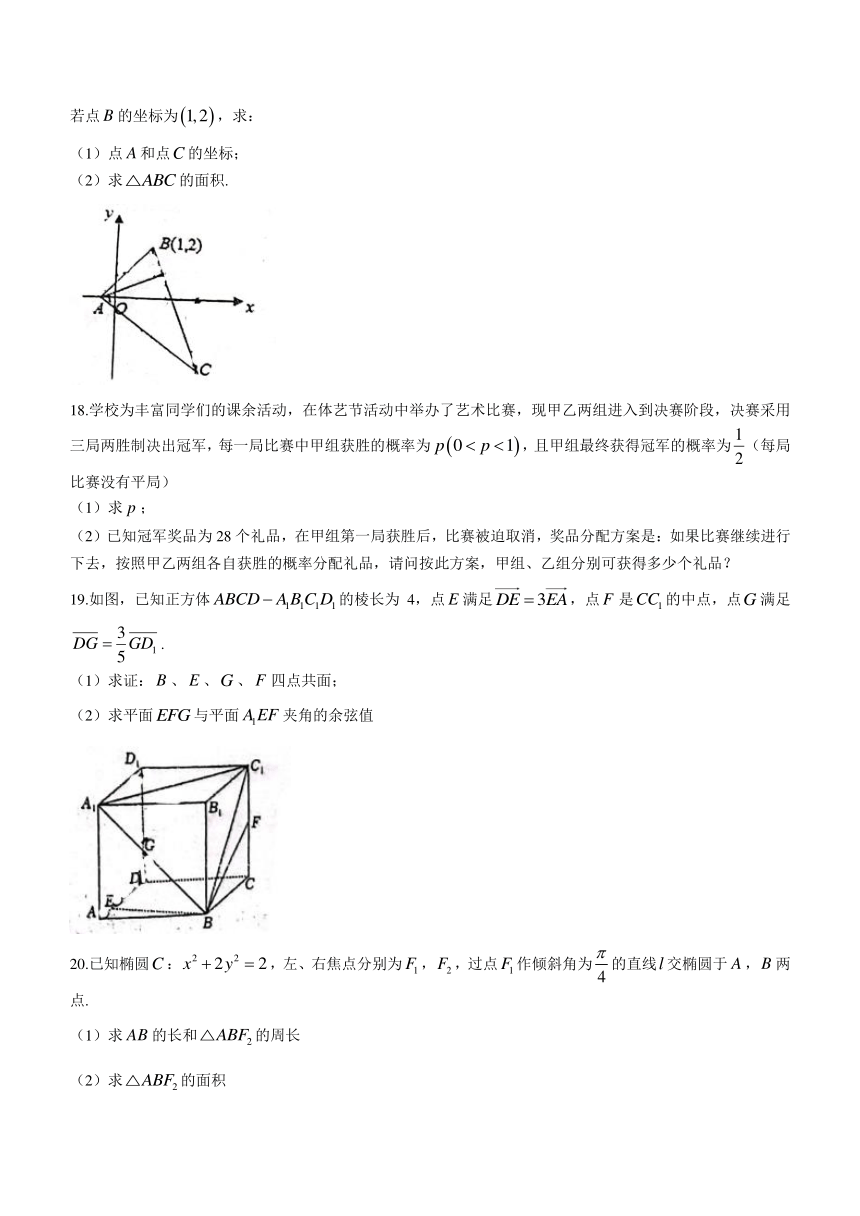
17.如图,在中,边上的高所在的直线方程为,的平分线所在的直线方程为,若点的坐标为,求:
(1)点和点的坐标;
(2)求的面积.
18.学校为丰富同学们的课余活动,在体艺节活动中举办了艺术比赛,现甲乙两组进入到决赛阶段,决赛采用三局两胜制决出冠军,每一局比赛中甲组获胜的概率为,且甲组最终获得冠军的概率为(每局比赛没有平局)
(1)求;
(2)已知冠军奖品为28个礼品,在甲组第一局获胜后,比赛被迫取消,奖品分配方案是:如果比赛继续进行下去,按照甲乙两组各自获胜的概率分配礼品,请问按此方案,甲组、乙组分别可获得多少个礼品?
19.如图,已知正方体的棱长为4,点满足,点是的中点,点满足.
(1)求证:、、、四点共面;
(2)求平面与平面夹角的余弦值
20.已知椭圆:,左、右焦点分别为,,过点作倾斜角为的直线交椭圆于,两点.
(1)求的长和的周长
(2)求的面积
21.已知圆经过点,两点,且圆心在直线上.
(1)求圆的方程;
(2)已知、是过点且互相垂直的两条直线,且与交于,两点,于交于、两点,求四边形面积的最大值.
22.如图,在四棱锥中,底面是边长为2的菱形,,为正三角形,为的中点,且平面平面,是线段上的点.
(1)求证:;
(2)是否存在点,使得直线与平面的夹角的正弦值为,若存在;求出此时的值;若不存在,请说明理由.
参考答案
一.选择题
1.解:根据函数的图象:,;故.故选:B
2.解:在一个不透明的袋中有4个红球和个黑球,现从袋中有放回地随机摸出2个球,
已知取出的球中至少有一个红球的概率为,则,
∴
∴,解得.故选:B.
3.解:在空间四边形中,,,,,点为的中点,
则
.
故选:B.
4.解:根据题意,方程表示的曲线是椭圆,
则,解可得:,且,故的取值范围为
故选:B.
5.解:,,可得,
,,则,
由,可得,可得直线与的夹角为,故选:B.
6.解:化圆为,可得圆心坐标为,半径为3.
由圆的弦的性质可得,最长的弦即圆的直径,的长为6.
∵点,∴.
弦最短时,弦和垂直,且经过点,此时.
故四边形的面积为.故选:B.
7.解:由事件定义,事件与事件可以同时发生,故不互为对立事件,A错误;
抛掷一枚骰子两次的样本点数共36种,
事件的样本点为,,,,,,,,,,,,,,,,,共18种,
事件的样本点为,,,,,,,,,,,共有12种,
事件的样本点为,,,,,共6种,
所以,B错误;
,C正确;
因为,所以事件与事件相互独立,D错误.
故选:C
8.解:由题设,建立如图所示的空间直角坐标系,设正方体的棱长为1,
则有,,,
∴,∴设,
∴,
由图知不是平角,∴为钝角等价于,
∴
∴,解得,
∴的取值范围是.故选:C.
二.多选题
9.【答案】BD
【详解】对于A,,是两个随机事件,且,
当,互斥时,则,故A错误;
对于B,若,,,则,
,所以事件与事件相互独立,故B正确:
对于C,事件“至多一次击中”包括:两次均未击中和两次击中一次,故C错误;
对于D,从1,2,3,4中任取2个不同的数,可能的情况有:,,,,,.
取出的2个数之差的绝对值为2的情况有:,,所以其概率为:,故D正确.
故选:BD.
10.【答案】ACD
【详解】对A,由题意,,故,,故A正确;
对B,的周长为,故B错误;
对C,若,则,即,故,故,故C正确;
对D,由余弦定理,
即,解得,故,故D正确;
故选:ACD
11.解:对于选项A,设圆的半径为,由题意可得圆的方程为(为整数),
根据点是圆上的点,且圆与直线:相切,
得,解得,或(舍去),
则圆的标准方程为,故A选项错误;
对于选项B,由选项A知圆的标准方程为,圆心,
因为点在圆上,且,所以线段为圆的直径,
因为直线:与圆相交于两点,
所以圆心在直线上,所以,解得,故B选项正确:
对于选项C,由选项知圆的半径为2,圆心,
则圆心到直线的距离,
因为,即,解得,
所以,解得或,
则直线的方程为或,故C选项正确;
对于选项D,直线的方程可化为,过定点,
由圆的性质可得,所以点的轨迹是以线段为直径的圆,
则此圆圆心为线段的中点,其坐标为,半径为,
则该圆的方程为,
由,得两圆的交点坐标为与,
故弦的中点的轨迹方程为,故D选项错误.
故选:BC.
12.【答案】BC
【详解】(向量法)为简化运算,建立空间直角坐标系如图,设正方体棱长为2,
,则,,,
,,故与不垂直,故A错误.
由知,,故B正确.
,为定值.故C正确.
又,,设平面的法向量,
由,,
令则,,∴
又平面的法向量,
∴
又,∴,∴.
故D错误.
三、填空题
13.【答案】
解:∵直线与轴、轴的交点坐标分别为,
椭圆的焦点在轴上,∴为椭圆的一个焦点,为椭圆的一个顶点,
∴,,,.故答案为:
14.【答案】
【详解】由题意可得,易知直线的一个方向向量为,
所以,点到直线的距离为
,故答案为:.
15.【答案】
【详解】因为,所以,
又,可得,
又因为事件,相互独立,所以.故答案为:
16.答案:
解:设,由可得,化简得,
即点在以原点为圆心,2为半径的圆上.又直线上存在点,
故直线与圆有公共点,因为圆心到直线的距离为,所以,所以.
四.解答题
17.解:(1)由,得顶点.又的斜率.
∵轴是的平分线 ,故的斜率为,所在直线的方程为
已知上的高所在直线的方程为①,
故的斜率为,所在直线的方程为②.
解①,②得顶点的坐标为;
(2),
又直线的方程是,到直线的距离.
∴的面积.
18.【解】(1)令事件:甲组在第局获胜,.甲组胜的概率为:
,解得.
(2)由题意知,左甲组第一局获 的情况下,甲组输掉比赛事件为:甲组接下来的比赛中连输两场,即,
即甲获胜的概率为,
故甲组、乙组应按照的比例来分配比赛奖品,
即甲组应获得21个礼品,乙组获得7个礼品比较合理.
19.解:(1)证明:如图,以为原点,,,所在直线为,,轴,建立空间直角坐标系
则,,,,
因为,
所以,所以、、、四点共面.
(2)由(1)知,,,
设平面的法向量为,
由,即,解得,
令,则,
同理可得平面的法向量,
设平面面夹角为,则.
所以面面夹角的余弦值为.
20.解:(1)椭圆:,,,
,即,
所以直线的方程为,
联立,得,或,
所以,
的周长为;
(2)由,得,由,得,
设,,的面积.
21.解:(1)根据题意,点,,
则线段的中垂线方程为,
圆心为直线和的交点,
则有,解得,
所以圆心的圆心坐标为,半径
所以圆心的方程为;
(2)根据题意,已知、是互相垂直的两条直线,分2种情况讨论:
①.当直线、其中一条直线斜率为0时,另一条斜率不存在.
不妨令的斜率为0,此时,
四边形的面积
②.当直线,斜率均存在时,设直线的斜率为
则其方程为,圆心到直线的距离为
于是,又的方程为
同理,
所以四边形的面积
当且仅当即时,等号成立.
综上所述,四边形面积的最大值为7.
22.解:(1)证明:连接,,
∵四边形是菱形,
∴,
∵,∴为等边三角形,
∵为的中点,∴,
∵是等边三角形,为的中点,
∴,
∵,∴平面,
∵平面,∴
∵,∴.
(2)∵平面平面,平面平面,
,平面,∴平面,
∵,以点为坐标原点,,,所在直线分别为,,轴建立空间直角坐标系,
则,,,,
设,
.
设平面的法向量,
,,,
由,取,得,
∵直线与平面的夹角的正弦值为,
∴.
整理得,由,解得,
∴存在点,使得直线与平面的夹角的正弦值为,.
一.选择题
1.如图,已知直线、、的斜率分别为、、,则、、的大小关系为( )
A. B. C. D.
2.在一个不透明的袋中有4个红球和个黑球,现从袋中有放回地随机摸出2个球,已知取出的球中至少有一个红球的概率为,则( )
A.1 B.2 C.3 D.4
3.如图,在空间四边形中,,,,点满足,点为的中点,则( )
A. B.
C. D.
4.已知方程表示的曲线是椭圆,则实数的取值范围是( )
A. B.
C. D.
5.若两异面直线与的方向向量分别是,,则直线与的夹角为( )
A. B. C. D.
6.在圆:内,过点的最长弦和最短弦分别是和,则四边形的面积为( )
A.24 B.12 C.10 D.8
7.抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件,“第二次向上的点数是奇数”为事件,“两次向上的点数之和能被3整除”为事件,则下列说法正确的是( )
A.事件与事件互为对立事件 B.
C. D.事件与事件相互不独立
8.已知动点在正方体的对角线(不含端点)上.设,若为钝角,则实数的取值范围为( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.设,是两个随机事件,且,,则
B.若,,,则事件与事件相互独立
C.一个人连续射击2次,事件“两次均未击中”与事件“至多一次击中”互为对立事件
D.从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是
10.已知椭圆:的左、右焦点分别为,,点在上,且的最大值为3,最小值为1,则( )
A.椭圆的圆心率为
B.的周长为4
C.若,则的面积为
D.若,则
11.已知经过点的圆的圆心坐标为(为整数),且与直线:相切,直线:与圆相交于、两点,下列说法正确的是( )
A.圆的标准方程为
B.若,则实数的值为
C.若,则直线的方程为或
D.弦的中点的轨迹方程为
12.如图,正方体中,为的中点,为棱上的动点,则下列结论正确的是( )
A.存在点,使平面
B.存在点,使
C.四面体的体积为定值
D.二面角的余弦值取值范围是
三、填空题
13.已知直线经过椭圆的一个焦点和一个顶点,则此椭圆的离心率______.
14.已知点,直线过原点,且平行于向量,则点到直线的距离是______.
15.已知事件,相互独立,且,,则______.
16.已知,,若直线上存在点,使得,则的取值范围是______.
四.解答题
17.如图,在中,边上的高所在的直线方程为,的平分线所在的直线方程为,若点的坐标为,求:
(1)点和点的坐标;
(2)求的面积.
18.学校为丰富同学们的课余活动,在体艺节活动中举办了艺术比赛,现甲乙两组进入到决赛阶段,决赛采用三局两胜制决出冠军,每一局比赛中甲组获胜的概率为,且甲组最终获得冠军的概率为(每局比赛没有平局)
(1)求;
(2)已知冠军奖品为28个礼品,在甲组第一局获胜后,比赛被迫取消,奖品分配方案是:如果比赛继续进行下去,按照甲乙两组各自获胜的概率分配礼品,请问按此方案,甲组、乙组分别可获得多少个礼品?
19.如图,已知正方体的棱长为4,点满足,点是的中点,点满足.
(1)求证:、、、四点共面;
(2)求平面与平面夹角的余弦值
20.已知椭圆:,左、右焦点分别为,,过点作倾斜角为的直线交椭圆于,两点.
(1)求的长和的周长
(2)求的面积
21.已知圆经过点,两点,且圆心在直线上.
(1)求圆的方程;
(2)已知、是过点且互相垂直的两条直线,且与交于,两点,于交于、两点,求四边形面积的最大值.
22.如图,在四棱锥中,底面是边长为2的菱形,,为正三角形,为的中点,且平面平面,是线段上的点.
(1)求证:;
(2)是否存在点,使得直线与平面的夹角的正弦值为,若存在;求出此时的值;若不存在,请说明理由.
参考答案
一.选择题
1.解:根据函数的图象:,;故.故选:B
2.解:在一个不透明的袋中有4个红球和个黑球,现从袋中有放回地随机摸出2个球,
已知取出的球中至少有一个红球的概率为,则,
∴
∴,解得.故选:B.
3.解:在空间四边形中,,,,,点为的中点,
则
.
故选:B.
4.解:根据题意,方程表示的曲线是椭圆,
则,解可得:,且,故的取值范围为
故选:B.
5.解:,,可得,
,,则,
由,可得,可得直线与的夹角为,故选:B.
6.解:化圆为,可得圆心坐标为,半径为3.
由圆的弦的性质可得,最长的弦即圆的直径,的长为6.
∵点,∴.
弦最短时,弦和垂直,且经过点,此时.
故四边形的面积为.故选:B.
7.解:由事件定义,事件与事件可以同时发生,故不互为对立事件,A错误;
抛掷一枚骰子两次的样本点数共36种,
事件的样本点为,,,,,,,,,,,,,,,,,共18种,
事件的样本点为,,,,,,,,,,,共有12种,
事件的样本点为,,,,,共6种,
所以,B错误;
,C正确;
因为,所以事件与事件相互独立,D错误.
故选:C
8.解:由题设,建立如图所示的空间直角坐标系,设正方体的棱长为1,
则有,,,
∴,∴设,
∴,
由图知不是平角,∴为钝角等价于,
∴
∴,解得,
∴的取值范围是.故选:C.
二.多选题
9.【答案】BD
【详解】对于A,,是两个随机事件,且,
当,互斥时,则,故A错误;
对于B,若,,,则,
,所以事件与事件相互独立,故B正确:
对于C,事件“至多一次击中”包括:两次均未击中和两次击中一次,故C错误;
对于D,从1,2,3,4中任取2个不同的数,可能的情况有:,,,,,.
取出的2个数之差的绝对值为2的情况有:,,所以其概率为:,故D正确.
故选:BD.
10.【答案】ACD
【详解】对A,由题意,,故,,故A正确;
对B,的周长为,故B错误;
对C,若,则,即,故,故,故C正确;
对D,由余弦定理,
即,解得,故,故D正确;
故选:ACD
11.解:对于选项A,设圆的半径为,由题意可得圆的方程为(为整数),
根据点是圆上的点,且圆与直线:相切,
得,解得,或(舍去),
则圆的标准方程为,故A选项错误;
对于选项B,由选项A知圆的标准方程为,圆心,
因为点在圆上,且,所以线段为圆的直径,
因为直线:与圆相交于两点,
所以圆心在直线上,所以,解得,故B选项正确:
对于选项C,由选项知圆的半径为2,圆心,
则圆心到直线的距离,
因为,即,解得,
所以,解得或,
则直线的方程为或,故C选项正确;
对于选项D,直线的方程可化为,过定点,
由圆的性质可得,所以点的轨迹是以线段为直径的圆,
则此圆圆心为线段的中点,其坐标为,半径为,
则该圆的方程为,
由,得两圆的交点坐标为与,
故弦的中点的轨迹方程为,故D选项错误.
故选:BC.
12.【答案】BC
【详解】(向量法)为简化运算,建立空间直角坐标系如图,设正方体棱长为2,
,则,,,
,,故与不垂直,故A错误.
由知,,故B正确.
,为定值.故C正确.
又,,设平面的法向量,
由,,
令则,,∴
又平面的法向量,
∴
又,∴,∴.
故D错误.
三、填空题
13.【答案】
解:∵直线与轴、轴的交点坐标分别为,
椭圆的焦点在轴上,∴为椭圆的一个焦点,为椭圆的一个顶点,
∴,,,.故答案为:
14.【答案】
【详解】由题意可得,易知直线的一个方向向量为,
所以,点到直线的距离为
,故答案为:.
15.【答案】
【详解】因为,所以,
又,可得,
又因为事件,相互独立,所以.故答案为:
16.答案:
解:设,由可得,化简得,
即点在以原点为圆心,2为半径的圆上.又直线上存在点,
故直线与圆有公共点,因为圆心到直线的距离为,所以,所以.
四.解答题
17.解:(1)由,得顶点.又的斜率.
∵轴是的平分线 ,故的斜率为,所在直线的方程为
已知上的高所在直线的方程为①,
故的斜率为,所在直线的方程为②.
解①,②得顶点的坐标为;
(2),
又直线的方程是,到直线的距离.
∴的面积.
18.【解】(1)令事件:甲组在第局获胜,.甲组胜的概率为:
,解得.
(2)由题意知,左甲组第一局获 的情况下,甲组输掉比赛事件为:甲组接下来的比赛中连输两场,即,
即甲获胜的概率为,
故甲组、乙组应按照的比例来分配比赛奖品,
即甲组应获得21个礼品,乙组获得7个礼品比较合理.
19.解:(1)证明:如图,以为原点,,,所在直线为,,轴,建立空间直角坐标系
则,,,,
因为,
所以,所以、、、四点共面.
(2)由(1)知,,,
设平面的法向量为,
由,即,解得,
令,则,
同理可得平面的法向量,
设平面面夹角为,则.
所以面面夹角的余弦值为.
20.解:(1)椭圆:,,,
,即,
所以直线的方程为,
联立,得,或,
所以,
的周长为;
(2)由,得,由,得,
设,,的面积.
21.解:(1)根据题意,点,,
则线段的中垂线方程为,
圆心为直线和的交点,
则有,解得,
所以圆心的圆心坐标为,半径
所以圆心的方程为;
(2)根据题意,已知、是互相垂直的两条直线,分2种情况讨论:
①.当直线、其中一条直线斜率为0时,另一条斜率不存在.
不妨令的斜率为0,此时,
四边形的面积
②.当直线,斜率均存在时,设直线的斜率为
则其方程为,圆心到直线的距离为
于是,又的方程为
同理,
所以四边形的面积
当且仅当即时,等号成立.
综上所述,四边形面积的最大值为7.
22.解:(1)证明:连接,,
∵四边形是菱形,
∴,
∵,∴为等边三角形,
∵为的中点,∴,
∵是等边三角形,为的中点,
∴,
∵,∴平面,
∵平面,∴
∵,∴.
(2)∵平面平面,平面平面,
,平面,∴平面,
∵,以点为坐标原点,,,所在直线分别为,,轴建立空间直角坐标系,
则,,,,
设,
.
设平面的法向量,
,,,
由,取,得,
∵直线与平面的夹角的正弦值为,
∴.
整理得,由,解得,
∴存在点,使得直线与平面的夹角的正弦值为,.
同课章节目录
