人教版六年级数学上册 第5单元《圆的面积》课件(共24张PPT)
文档属性
| 名称 | 人教版六年级数学上册 第5单元《圆的面积》课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 50.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 13:03:20 | ||
图片预览




文档简介
(共24张PPT)
圆的面积
圆的面积
新 知
分析
实 践
结论
应 用
寸也是一种长度单位,
1英寸=2.54厘米
9寸
6寸
6+6=12>9
9寸
6寸
<
+
你们能帮帮她么?
新 知
分析
实 践
结论
应 用
2. 引出主题
解决这个问题,需要求出圆的面积
圆形的面积
是指哪一部分的面积?
新 知
分析
实 践
结论
应 用
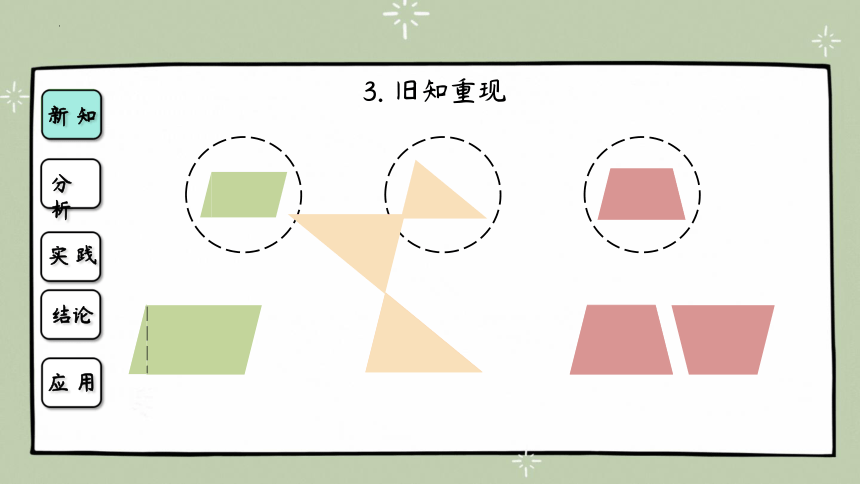
3. 旧知重现
新 知
分析
实 践
结论
应 用
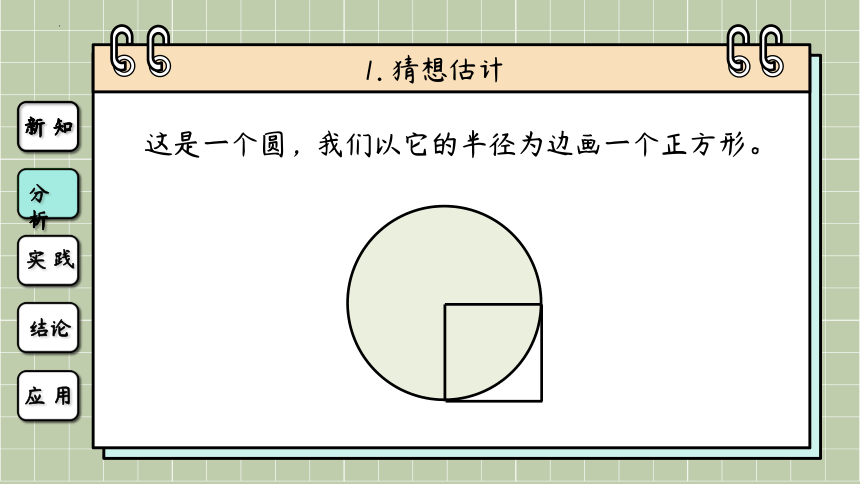
1. 猜想估计
这是一个圆,我们以它的半径为边画一个正方形。
新 知
分析
实 践
结论
应 用
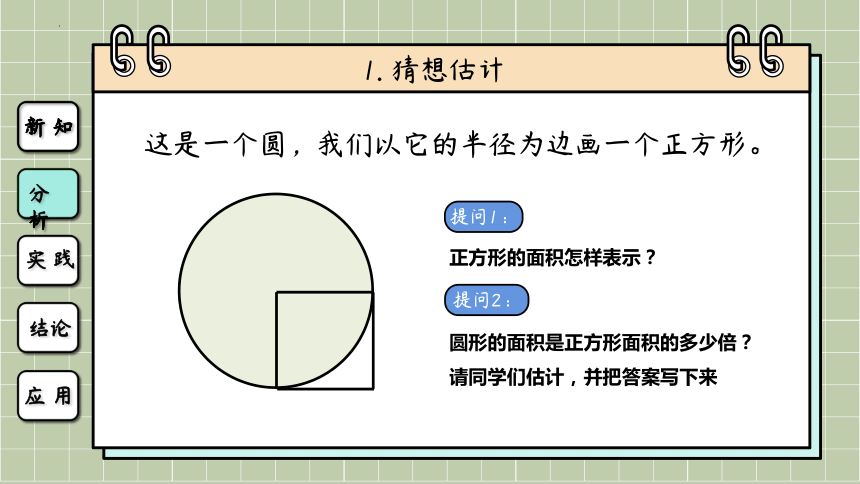
1. 猜想估计
这是一个圆,我们以它的半径为边画一个正方形。
正方形的面积怎样表示?
圆形的面积是正方形面积的多少倍?
请同学们估计,并把答案写下来
提问1:
提问2:
新 知
分析
实 践
结论
应 用
2. 类比推导
说一说有什么办法,可以用来求圆形的面积?
新 知
分析
实 践
结论
应 用
2. 类比推导
说一说有什么办法,可以用来求圆形的面积?
①剪、拼——
平行四边形面积的推导就是先沿高剪开,然后再拼成已学过的长方形来推导出平行四边形的面积公式的。
②旋转、移拼——
三角形、梯形面积的推导就是通过旋转,然后再移拼成已学的平行四边形来推导出面积公式的。
新 知
分析
实 践
结论
应 用
学习总是化未知为已知;求一个新的图形的面积时也是把新图形转化成已知图形来求面积。
1. 总结方法
说一说有什么办法,可以用来求圆形的面积?
①剪、拼——
平行四边形面积的推导就是先沿高剪开,然后再拼成已学过的长方形来推导出平行四边形的面积公式的。
②旋转、移拼——
三角形、梯形面积的推导就是通过旋转,然后再移拼成已学的平行四边形来推导出面积公式的。
新 知
分析
实 践
结论
应 用
1. 总结方法
哪个面积大?为什么?圆的面积与什么有关?
新 知
分析
实 践
结论
应 用
2. 总结规律
提示: 在剪的时候,不能随意剪,要沿半径剪,并且要等分。先从最少的情况来研究:把圆两等分再拼。在此基础上继续四等分。
四等分
新 知
分析
实 践
结论
应 用
2. 总结规律
八等分
新 知
分析
实 践
结论
应 用
2. 总结规律
十六等分
总结:
在不断切的过程中,越来越像一个平行四边形,如果继续无限分下去,会怎样?
新 知
分析
实 践
结论
应 用
2. 总结规律
2. 总结规律
新 知
分析
实 践
结论
应 用
1. 总结公式
提问1:
转化后,长方形的宽是圆形的什么?
提问2:
转化后,长方形的长是圆形的什么?
新 知
分析
实 践
结论
应 用
1. 总结公式
长方形的长相当于圆的 ,
宽相当于圆的 。
r
r
πr
πr
新 知
分析
实 践
结论
应 用
2. 展示公式
长方形的面积 = 长 × 宽
S = πr(C/2) × r
圆的面积 =圆周长的一半 × 半径
C
r
r
πr
πr
S = πr
≈ 3.14
= π
r
S圆
新 知
分析
实 践
结论
应 用
1. 课堂小练
9寸
6寸
S圆 = πr ,π取 3.14
两个披萨的半径:
9÷2 = 4.5(英寸)
6÷2 = 3(英寸)
9寸披萨面积:
3.14×4.5 = 63.585(英寸 )
2个6寸披萨面积:
2×3.14×3 = 56.52(英寸 )
63.585 > 56.52
新 知
分析
实 践
结论
应 用
只需要知道圆形的半径,就可以求出圆形的面积。所以圆形的面积只跟它的半径有关!
圆面积公式的历史
开普勒是德国天文学家,他发现了行星运动的三大定律。为哥白尼的日心说提供了最可靠的证据,是现代实验光学的奠基人。开普勒第一次尝试把圆分割成许多小扇形,所以这才有了我们所熟悉的圆面积公式。开普勒运用无穷分割法,求出了许多图形的面积。1615年,他将自己创造的这种求圆面积的新方法,发表在《葡萄酒桶的立体几何》一书中。《葡萄酒桶的立体几何》一书,很快在欧洲流传开了。数学家们高度评价开普勒的工作,称赞这本书是人们创造求圆面积和体积新方法的灵感源泉。
圆的面积
同学们
同学们
再见
再见
!
!
,
,
圆的面积
圆的面积
新 知
分析
实 践
结论
应 用
寸也是一种长度单位,
1英寸=2.54厘米
9寸
6寸
6+6=12>9
9寸
6寸
<
+
你们能帮帮她么?
新 知
分析
实 践
结论
应 用
2. 引出主题
解决这个问题,需要求出圆的面积
圆形的面积
是指哪一部分的面积?
新 知
分析
实 践
结论
应 用
3. 旧知重现
新 知
分析
实 践
结论
应 用
1. 猜想估计
这是一个圆,我们以它的半径为边画一个正方形。
新 知
分析
实 践
结论
应 用
1. 猜想估计
这是一个圆,我们以它的半径为边画一个正方形。
正方形的面积怎样表示?
圆形的面积是正方形面积的多少倍?
请同学们估计,并把答案写下来
提问1:
提问2:
新 知
分析
实 践
结论
应 用
2. 类比推导
说一说有什么办法,可以用来求圆形的面积?
新 知
分析
实 践
结论
应 用
2. 类比推导
说一说有什么办法,可以用来求圆形的面积?
①剪、拼——
平行四边形面积的推导就是先沿高剪开,然后再拼成已学过的长方形来推导出平行四边形的面积公式的。
②旋转、移拼——
三角形、梯形面积的推导就是通过旋转,然后再移拼成已学的平行四边形来推导出面积公式的。
新 知
分析
实 践
结论
应 用
学习总是化未知为已知;求一个新的图形的面积时也是把新图形转化成已知图形来求面积。
1. 总结方法
说一说有什么办法,可以用来求圆形的面积?
①剪、拼——
平行四边形面积的推导就是先沿高剪开,然后再拼成已学过的长方形来推导出平行四边形的面积公式的。
②旋转、移拼——
三角形、梯形面积的推导就是通过旋转,然后再移拼成已学的平行四边形来推导出面积公式的。
新 知
分析
实 践
结论
应 用
1. 总结方法
哪个面积大?为什么?圆的面积与什么有关?
新 知
分析
实 践
结论
应 用
2. 总结规律
提示: 在剪的时候,不能随意剪,要沿半径剪,并且要等分。先从最少的情况来研究:把圆两等分再拼。在此基础上继续四等分。
四等分
新 知
分析
实 践
结论
应 用
2. 总结规律
八等分
新 知
分析
实 践
结论
应 用
2. 总结规律
十六等分
总结:
在不断切的过程中,越来越像一个平行四边形,如果继续无限分下去,会怎样?
新 知
分析
实 践
结论
应 用
2. 总结规律
2. 总结规律
新 知
分析
实 践
结论
应 用
1. 总结公式
提问1:
转化后,长方形的宽是圆形的什么?
提问2:
转化后,长方形的长是圆形的什么?
新 知
分析
实 践
结论
应 用
1. 总结公式
长方形的长相当于圆的 ,
宽相当于圆的 。
r
r
πr
πr
新 知
分析
实 践
结论
应 用
2. 展示公式
长方形的面积 = 长 × 宽
S = πr(C/2) × r
圆的面积 =圆周长的一半 × 半径
C
r
r
πr
πr
S = πr
≈ 3.14
= π
r
S圆
新 知
分析
实 践
结论
应 用
1. 课堂小练
9寸
6寸
S圆 = πr ,π取 3.14
两个披萨的半径:
9÷2 = 4.5(英寸)
6÷2 = 3(英寸)
9寸披萨面积:
3.14×4.5 = 63.585(英寸 )
2个6寸披萨面积:
2×3.14×3 = 56.52(英寸 )
63.585 > 56.52
新 知
分析
实 践
结论
应 用
只需要知道圆形的半径,就可以求出圆形的面积。所以圆形的面积只跟它的半径有关!
圆面积公式的历史
开普勒是德国天文学家,他发现了行星运动的三大定律。为哥白尼的日心说提供了最可靠的证据,是现代实验光学的奠基人。开普勒第一次尝试把圆分割成许多小扇形,所以这才有了我们所熟悉的圆面积公式。开普勒运用无穷分割法,求出了许多图形的面积。1615年,他将自己创造的这种求圆面积的新方法,发表在《葡萄酒桶的立体几何》一书中。《葡萄酒桶的立体几何》一书,很快在欧洲流传开了。数学家们高度评价开普勒的工作,称赞这本书是人们创造求圆面积和体积新方法的灵感源泉。
圆的面积
同学们
同学们
再见
再见
!
!
,
,
