2023-2024学年冀教版数学八年级上册第十七章特殊三角形全章强化训练(含解析)
文档属性
| 名称 | 2023-2024学年冀教版数学八年级上册第十七章特殊三角形全章强化训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 10:04:49 | ||
图片预览



文档简介
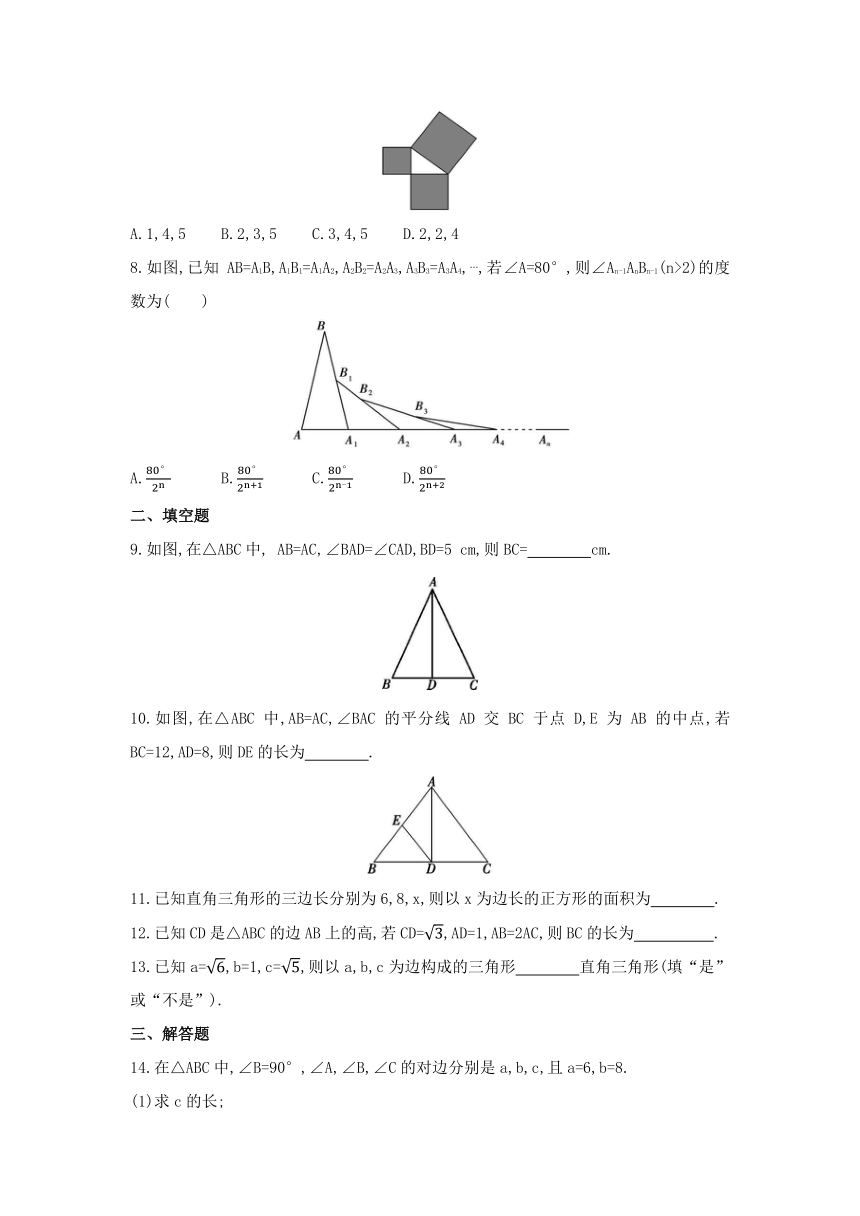
《第十七章 特殊三角形》全章强化训练
一、选择题
1.如图,在△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为 ( )
A.18° B.20° C.30° D.36°
2.如图,在△ABC中,AB=AC,AD,CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是 ( )
A.20° B.35° C.40° D.70°
5.如图,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE= ( )
A.10° B.15° C.20° D.25°
6.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为 ( )
A.3 B.4 C.5 D.6
7.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
8.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4, ,若∠A=80°,则∠An-1AnBn-1(n>2)的度数为( )
A. B. C. D.
二、填空题
9.如图,在△ABC中, AB=AC,∠BAD=∠CAD,BD=5 cm,则BC= cm.
10.如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为 .
11.已知直角三角形的三边长分别为6,8,x,则以x为边长的正方形的面积为 .
12.已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 .
13.已知a=,b=1,c=,则以a,b,c为边构成的三角形 直角三角形(填“是”或“不是”).
三、解答题
14.在△ABC中,∠B=90°,∠A,∠B,∠C的对边分别是a,b,c,且a=6,b=8.
(1)求c的长;
(2)求斜边上的高.
15.如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.
(1)△AMN是否是等腰三角形 说明理由.
(2)点P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.
①求证:△BPM是等腰三角形.
②若△ABC的周长为a,BC=b(a>2b),直接写出△AMN的周长(用含a,b的式子表示).
16.如图,在△ABC中,∠ABC=90°,AC=25 cm,BC=15 cm.
(1)直接写出AB的长度;
(2)若点P在AB上,∠PAC=∠PCA ,求AP的长;
(3)设点M在AC上,若△MBC为等腰三角形,直接写出AM的长.
17.如图,在边长为2的等边三角形ABC中,D是BC的中点,点E在线段AD上,连接BE,在BE的下方作等边三角形BEF,连接DF,当△BDF的周长最小时,求∠DBF的度数.
18.在△ABC中,BC=a,AC=b,AB=c,设c为最长边.当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为 三角形;当△ABC三边长分别为6,8,11时,△ABC为 三角形.
(2)小明同学根据上述探究,有下面的猜想:“当a2+b2>c2时,△ABC为锐角三角形;当a2+b2当a=2,b=4时,最长边c分别在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形
参考答案
一、选择题
1.A 【解析】 因为DA⊥AC,所以∠DAC=90°.因为AB=AC,所以∠B=∠C.因为∠B+∠C+∠BAC=180°,∠B=2∠BAD,所以2∠BAD+2∠BAD+∠BAD+∠DAC =180°,所以5∠BAD=90°,所以∠BAD=18°.故选A.
2.B 【解析】 ∵AB=AC,AD是△ABC的中线,∴∠BAD=∠CAD=20°,∠ABC=∠ACB,∴∠ACB
=×(180°-40°)=70°.∵CE是△ABC的角平分线,∴∠ACE=∠ACB=35°.故选B.
5.C 【解析】 在等边三角形ABC中, AD⊥BC,∴AD所在直线是BC的线段垂直平分线.∵E是AD上一点,∴EB=EC,∴∠EBD=∠ECD.∵∠CED=50°,∴∠ECD=40°,∴∠EBC=
40°,又∵∠ABC=60°,∴∠ABE=60°-40°=20°.故选C.
6.D 【解析】 因为△ABC与△DCE都是等边三角形,所以∠ACB=∠BAC=∠DCE=60°,DC=DE,AC=AB=3,所以∠ACD=180°-∠ACB-∠DCE=60°,因为∠BAD=150°,所以∠CAD=∠BAD-∠BAC=90°,所以∠ADC=90°-∠ACD=30°,所以DC=2AC=2×3=6,所以DE=DC=6 .故选D.
7.B 【解析】 设选取的三块纸片的面积分别为a,b,c(a≤b8.C 【解析】 在△ABA1中,∠A=80°,AB=A1B,∴∠BA1A=80°.∵A1A2=A1B1,∠BA1A是△A1A2B1的外角,∴∠B1A2A1=,同理可得,∠B2A3A2=,∠B3A4A3=, ,∴∠An-1AnBn-1=.故选C.
二、填空题
9.10 【解析】 因为AB=AC, ∠BAD=∠CAD,所以BC=2BD.因为BD=5 cm ,所以BC=2BD=10 cm.
10.5 【解析】 ∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=6,∴∠ADB=90°,∴AB=
=10.∵E为AB的中点,∴DE=AB=5.
11.100或28 【解析】 当8是直角边长时,根据勾股定理,得x2=62+82=36+64=100,所以以x为边长的正方形的面积为100;当8是斜边长时,根据勾股定理,得x2=82-62=64-36=28,所以以x为边长的正方形的面积为28.综上,以x为边长的正方形的面积为100或28.
12.2或2 【解析】 分两种情况:①当CD在△ABC内部时,如图1,∵CD⊥AB,∴∠CDA=90°,∵CD=,AD=1,∴AC==2,∵AB=2AC,∴AB=4,∴BD=4-1=3,∴BC==2;②当CD在△ABC外部时,如图2,同理,可得AC=2,AB=4,∴BD=4+1=5,∴BC==2.综上,BC的长为2或2.
13.是 【解析】 ∵c2+b2=()2+12=6,a2=()2=6,∴c2+b2=a2,∴以a,b,c为边构成的三角形是直角三角形.
三、解答题
14.【解析】 (1)在△ABC中,∠B=90°,∠A,∠B,∠C的对边分别是a,b,c,且a=6,b=8,
∴c==2.
(2)设斜边上的高为h,则
S△ABC=×8×h=×6×2,
解得h=.
15.【解析】 (1)△AMN是等腰三角形.理由如下:
因为AB=AC,所以∠ABC=∠ACB.
因为MN∥BC,所以∠AMN=∠ABC,∠ANM=∠ACB,
所以∠AMN=∠ANM,所以AM=AN,所以△AMN是等腰三角形.
(2)①因为BP平分∠ABC ,所以∠PBC=∠PBM,
因为MN∥BC,所以∠MPB=∠PBC,所以∠PBM=∠MPB,
所以△BPM是等腰三角形.
②△AMN的周长为a-b.
因为△BPM是等腰三角形,所以MP=MB,
同理可得,NP=NC,
所以△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC,
又因为△ABC的周长为a,BC=b(a>2b),
所以AB+AC=a-b,所以△AMN的周长为a-b.
16.【解析】 (1)AB=20 cm.
在△ABC中,∠ABC=90°,AC=25 cm, BC=15 cm,
所以AB==20 cm.
(2)因为∠PAC=∠PCA,所以AP=PC,
设AP=PC=x cm, 则PB=(20-x)cm,
在△BPC中,∠PBC=90°,
由勾股定理,得(20-x)2+152=x2,解得x=,
所以AP= cm.
(3)AM的长为10 cm,7 cm或12.5 cm.
①当CM=BC=15 cm时,△MBC为等腰三角形,
所以AM=AC-CM=10 cm.
②当BM=BC=15 cm时,△MBC为等腰三角形,
如图,过点B作BH⊥AC于点H ,所以BH==12(cm),
所以CH==9 cm,所以AM=AC-2CH=7 cm .
③当BM=CM时,△MBC为等腰三角形,
设AM=x cm,则BM=CM=(25-x)cm,
在直角三角形BMH中,BM2=MH2+BH2,
所以(25-x)2=122+(25-x-9)2,
解得x=12.5,所以AM=12.5 cm,
综上所述,若△MBC为等腰三角形, AM的长为10 cm,7 cm,或12.5 cm.
17.【解析】 如图,连接CF,∵△ABC,△BEF都是等边三角形,
∴AB=BC=AC,BE=EF=BF,∠BAC=∠ABC=∠ACB=∠EBF=∠BEF=∠BFE=60°,
∴∠ABC-∠EBD=∠EBF-∠EBD,即∠ABE=∠CBF.
在△BAE和△BCF中,
∴△BAE≌△BCF(SAS),∴∠BCF=∠BAD.
∵D为BC的中点,∴∠BAD=∠BAC=30°,
∴∠BCF=30°.
如图,作点D关于CF的对称点G,连接CG,DG,则FD=FG,
∴当B,F,G在同一直线上时,DF+BF的最小值等于线段BG长,且BG⊥CG时,△BDF的周长最小,
由轴对称的性质,可得∠DCG=2∠BCF=60°,CD=CG,
∴△DCG是等边三角形,∴DG=DC=DB,
∴∠DBF=∠DGB=∠CDG=30°.
18.【解析】 (1)锐角 钝角
在直角三角形中,两直角边长分别为6,8时,斜边为=10,
∴当△ABC三边长分别为6,8,9时,△ABC为锐角三角形;
当△ABC三边长分别为6,8,11时,△ABC为钝角三角形.
(2)∵c为最长边,2+4=6,
∴4≤c<6,
a2+b2=22+42=20,
①a2+b2>c2,即c2<20,0∴当4≤c<2时,△ABC是锐角三角形;
②a2+b2=c2,即c2=20,c=2,
∴当c=2时,△ABC是直角三角形;
③a2+b220,c>2,
∴当2
一、选择题
1.如图,在△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为 ( )
A.18° B.20° C.30° D.36°
2.如图,在△ABC中,AB=AC,AD,CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是 ( )
A.20° B.35° C.40° D.70°
5.如图,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE= ( )
A.10° B.15° C.20° D.25°
6.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为 ( )
A.3 B.4 C.5 D.6
7.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
8.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4, ,若∠A=80°,则∠An-1AnBn-1(n>2)的度数为( )
A. B. C. D.
二、填空题
9.如图,在△ABC中, AB=AC,∠BAD=∠CAD,BD=5 cm,则BC= cm.
10.如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为 .
11.已知直角三角形的三边长分别为6,8,x,则以x为边长的正方形的面积为 .
12.已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 .
13.已知a=,b=1,c=,则以a,b,c为边构成的三角形 直角三角形(填“是”或“不是”).
三、解答题
14.在△ABC中,∠B=90°,∠A,∠B,∠C的对边分别是a,b,c,且a=6,b=8.
(1)求c的长;
(2)求斜边上的高.
15.如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.
(1)△AMN是否是等腰三角形 说明理由.
(2)点P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.
①求证:△BPM是等腰三角形.
②若△ABC的周长为a,BC=b(a>2b),直接写出△AMN的周长(用含a,b的式子表示).
16.如图,在△ABC中,∠ABC=90°,AC=25 cm,BC=15 cm.
(1)直接写出AB的长度;
(2)若点P在AB上,∠PAC=∠PCA ,求AP的长;
(3)设点M在AC上,若△MBC为等腰三角形,直接写出AM的长.
17.如图,在边长为2的等边三角形ABC中,D是BC的中点,点E在线段AD上,连接BE,在BE的下方作等边三角形BEF,连接DF,当△BDF的周长最小时,求∠DBF的度数.
18.在△ABC中,BC=a,AC=b,AB=c,设c为最长边.当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为 三角形;当△ABC三边长分别为6,8,11时,△ABC为 三角形.
(2)小明同学根据上述探究,有下面的猜想:“当a2+b2>c2时,△ABC为锐角三角形;当a2+b2
参考答案
一、选择题
1.A 【解析】 因为DA⊥AC,所以∠DAC=90°.因为AB=AC,所以∠B=∠C.因为∠B+∠C+∠BAC=180°,∠B=2∠BAD,所以2∠BAD+2∠BAD+∠BAD+∠DAC =180°,所以5∠BAD=90°,所以∠BAD=18°.故选A.
2.B 【解析】 ∵AB=AC,AD是△ABC的中线,∴∠BAD=∠CAD=20°,∠ABC=∠ACB,∴∠ACB
=×(180°-40°)=70°.∵CE是△ABC的角平分线,∴∠ACE=∠ACB=35°.故选B.
5.C 【解析】 在等边三角形ABC中, AD⊥BC,∴AD所在直线是BC的线段垂直平分线.∵E是AD上一点,∴EB=EC,∴∠EBD=∠ECD.∵∠CED=50°,∴∠ECD=40°,∴∠EBC=
40°,又∵∠ABC=60°,∴∠ABE=60°-40°=20°.故选C.
6.D 【解析】 因为△ABC与△DCE都是等边三角形,所以∠ACB=∠BAC=∠DCE=60°,DC=DE,AC=AB=3,所以∠ACD=180°-∠ACB-∠DCE=60°,因为∠BAD=150°,所以∠CAD=∠BAD-∠BAC=90°,所以∠ADC=90°-∠ACD=30°,所以DC=2AC=2×3=6,所以DE=DC=6 .故选D.
7.B 【解析】 设选取的三块纸片的面积分别为a,b,c(a≤b
二、填空题
9.10 【解析】 因为AB=AC, ∠BAD=∠CAD,所以BC=2BD.因为BD=5 cm ,所以BC=2BD=10 cm.
10.5 【解析】 ∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=6,∴∠ADB=90°,∴AB=
=10.∵E为AB的中点,∴DE=AB=5.
11.100或28 【解析】 当8是直角边长时,根据勾股定理,得x2=62+82=36+64=100,所以以x为边长的正方形的面积为100;当8是斜边长时,根据勾股定理,得x2=82-62=64-36=28,所以以x为边长的正方形的面积为28.综上,以x为边长的正方形的面积为100或28.
12.2或2 【解析】 分两种情况:①当CD在△ABC内部时,如图1,∵CD⊥AB,∴∠CDA=90°,∵CD=,AD=1,∴AC==2,∵AB=2AC,∴AB=4,∴BD=4-1=3,∴BC==2;②当CD在△ABC外部时,如图2,同理,可得AC=2,AB=4,∴BD=4+1=5,∴BC==2.综上,BC的长为2或2.
13.是 【解析】 ∵c2+b2=()2+12=6,a2=()2=6,∴c2+b2=a2,∴以a,b,c为边构成的三角形是直角三角形.
三、解答题
14.【解析】 (1)在△ABC中,∠B=90°,∠A,∠B,∠C的对边分别是a,b,c,且a=6,b=8,
∴c==2.
(2)设斜边上的高为h,则
S△ABC=×8×h=×6×2,
解得h=.
15.【解析】 (1)△AMN是等腰三角形.理由如下:
因为AB=AC,所以∠ABC=∠ACB.
因为MN∥BC,所以∠AMN=∠ABC,∠ANM=∠ACB,
所以∠AMN=∠ANM,所以AM=AN,所以△AMN是等腰三角形.
(2)①因为BP平分∠ABC ,所以∠PBC=∠PBM,
因为MN∥BC,所以∠MPB=∠PBC,所以∠PBM=∠MPB,
所以△BPM是等腰三角形.
②△AMN的周长为a-b.
因为△BPM是等腰三角形,所以MP=MB,
同理可得,NP=NC,
所以△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC,
又因为△ABC的周长为a,BC=b(a>2b),
所以AB+AC=a-b,所以△AMN的周长为a-b.
16.【解析】 (1)AB=20 cm.
在△ABC中,∠ABC=90°,AC=25 cm, BC=15 cm,
所以AB==20 cm.
(2)因为∠PAC=∠PCA,所以AP=PC,
设AP=PC=x cm, 则PB=(20-x)cm,
在△BPC中,∠PBC=90°,
由勾股定理,得(20-x)2+152=x2,解得x=,
所以AP= cm.
(3)AM的长为10 cm,7 cm或12.5 cm.
①当CM=BC=15 cm时,△MBC为等腰三角形,
所以AM=AC-CM=10 cm.
②当BM=BC=15 cm时,△MBC为等腰三角形,
如图,过点B作BH⊥AC于点H ,所以BH==12(cm),
所以CH==9 cm,所以AM=AC-2CH=7 cm .
③当BM=CM时,△MBC为等腰三角形,
设AM=x cm,则BM=CM=(25-x)cm,
在直角三角形BMH中,BM2=MH2+BH2,
所以(25-x)2=122+(25-x-9)2,
解得x=12.5,所以AM=12.5 cm,
综上所述,若△MBC为等腰三角形, AM的长为10 cm,7 cm,或12.5 cm.
17.【解析】 如图,连接CF,∵△ABC,△BEF都是等边三角形,
∴AB=BC=AC,BE=EF=BF,∠BAC=∠ABC=∠ACB=∠EBF=∠BEF=∠BFE=60°,
∴∠ABC-∠EBD=∠EBF-∠EBD,即∠ABE=∠CBF.
在△BAE和△BCF中,
∴△BAE≌△BCF(SAS),∴∠BCF=∠BAD.
∵D为BC的中点,∴∠BAD=∠BAC=30°,
∴∠BCF=30°.
如图,作点D关于CF的对称点G,连接CG,DG,则FD=FG,
∴当B,F,G在同一直线上时,DF+BF的最小值等于线段BG长,且BG⊥CG时,△BDF的周长最小,
由轴对称的性质,可得∠DCG=2∠BCF=60°,CD=CG,
∴△DCG是等边三角形,∴DG=DC=DB,
∴∠DBF=∠DGB=∠CDG=30°.
18.【解析】 (1)锐角 钝角
在直角三角形中,两直角边长分别为6,8时,斜边为=10,
∴当△ABC三边长分别为6,8,9时,△ABC为锐角三角形;
当△ABC三边长分别为6,8,11时,△ABC为钝角三角形.
(2)∵c为最长边,2+4=6,
∴4≤c<6,
a2+b2=22+42=20,
①a2+b2>c2,即c2<20,0
②a2+b2=c2,即c2=20,c=2,
∴当c=2时,△ABC是直角三角形;
③a2+b2
∴当2
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
