12.4 综合与实践 一次函数模型的应用分层练习(含答案)
文档属性
| 名称 | 12.4 综合与实践 一次函数模型的应用分层练习(含答案) | 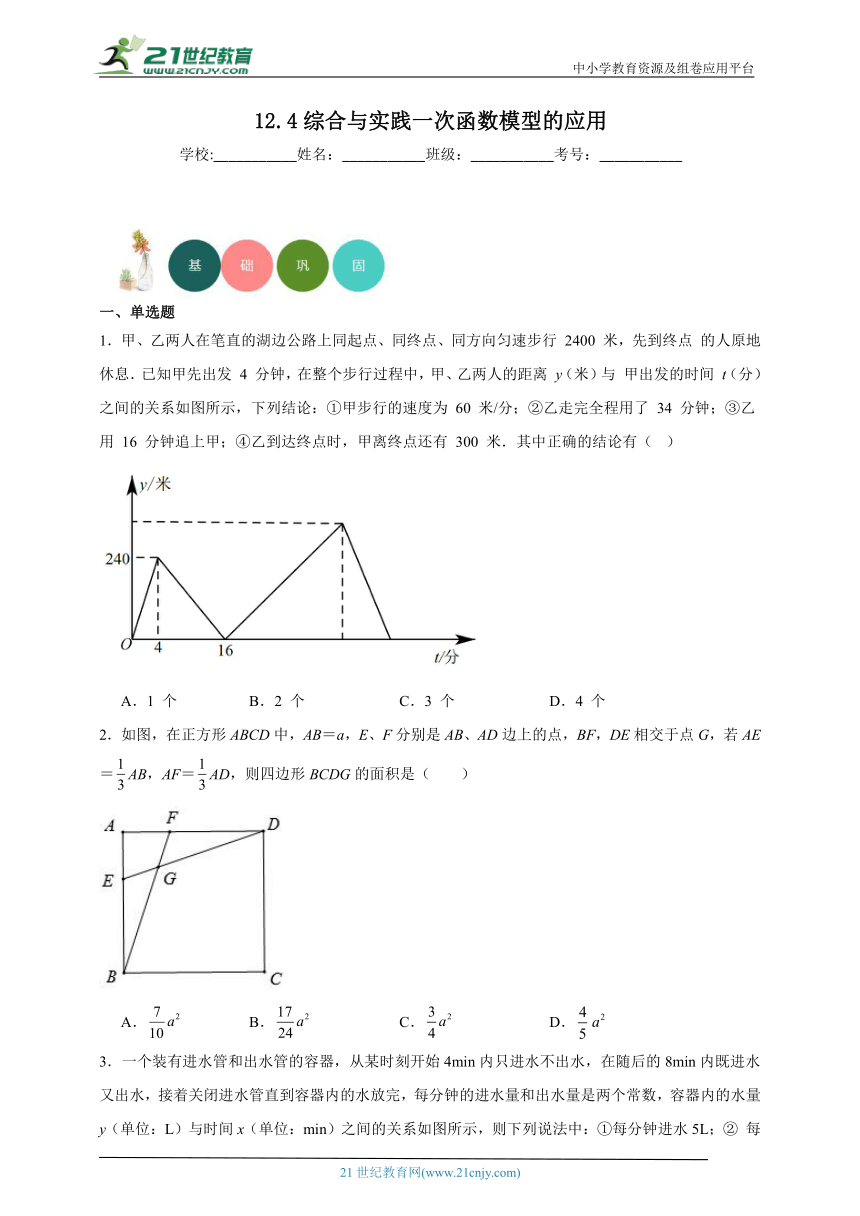 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 21:40:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.4综合与实践一次函数模型的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行 2400 米,先到终点 的人原地休息.已知甲先出发 4 分钟,在整个步行过程中,甲、乙两人的距离 y(米)与 甲出发的时间 t(分)之间的关系如图所示,下列结论:①甲步行的速度为 60 米/分;②乙走完全程用了 34 分钟;③乙用 16 分钟追上甲;④乙到达终点时,甲离终点还有 300 米.其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4 个
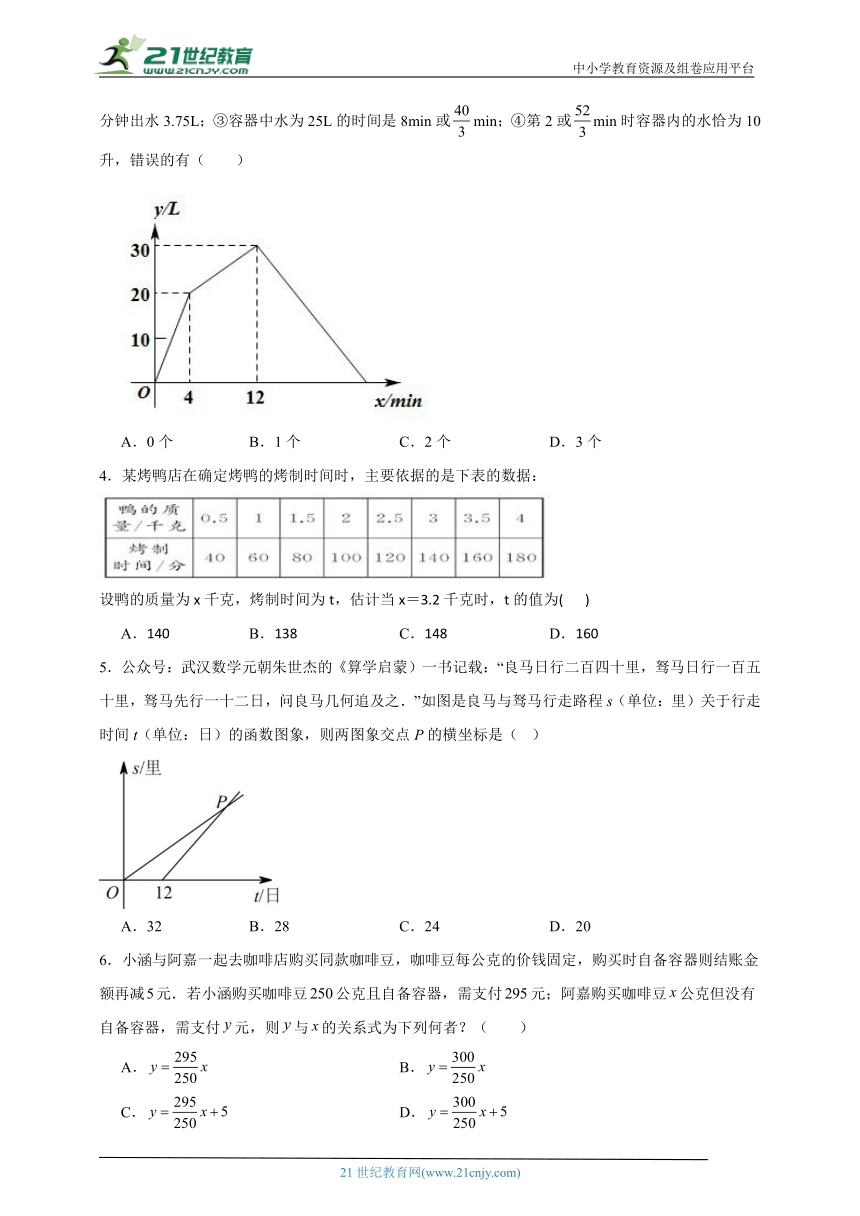
2.如图,在正方形ABCD中,AB=a,E、F分别是AB、AD边上的点,BF,DE相交于点G,若AE=AB,AF=AD,则四边形BCDG的面积是( )
A. B. C. D.
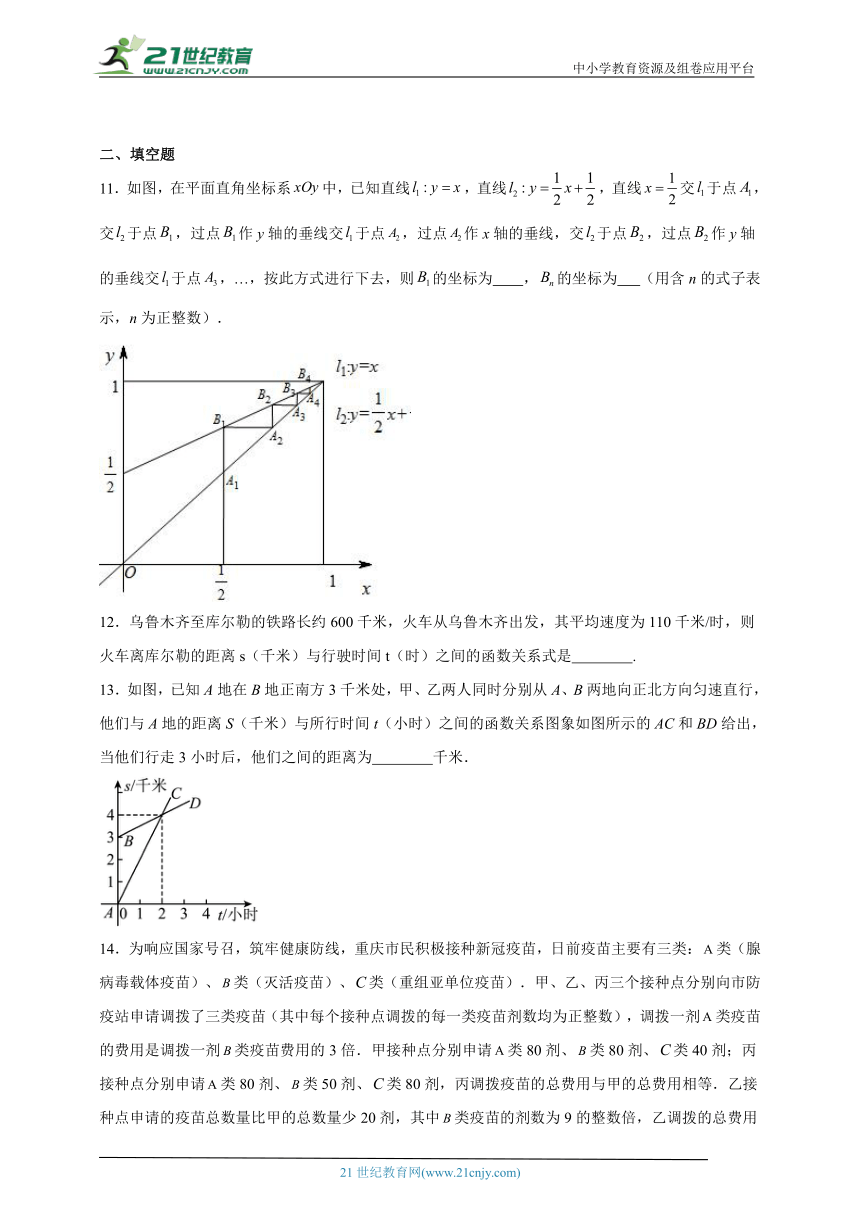
3.一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则下列说法中:①每分钟进水5L;② 每分钟出水3.75L;③容器中水为25L的时间是8min或min;④第2或min时容器内的水恰为10升,错误的有( )
A.0个 B.1个 C.2个 D.3个
4.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为( )
A.140 B.138 C.148 D.160
5.公众号:武汉数学元朝朱世杰的《算学启蒙)一书记载:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”如图是良马与驽马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象,则两图象交点P的横坐标是( )
A.32 B.28 C.24 D.20
6.小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结账金额再减元.若小涵购买咖啡豆公克且自备容器,需支付元;阿嘉购买咖啡豆公克但没有自备容器,需支付元,则与的关系式为下列何者?( )
A. B.
C. D.
7.东东和爸爸一起往华中公园方向去旅游,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,东东继续前行,5分钟后也原路返回,两人恰好同时到家.东东和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论中错误的是( )
A.两人前行过程中的速度为200米/分
B.m的值是15,n的值是3000
C.东东开始返回时与爸爸相距1800米
D.运动18分钟或30分钟时,两人相距900米
8.如图,直线PA是一次函数的图象,直线PB是一次函数的图象,若PA与轴交于点Q,且,则的值分别是( )
A. B.2,1 C. D.
9.如图,直线y=﹣x+2与x轴.y轴分别交于A.B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( ).
A.(,3) B.(,) C.(2,2) D.(2,4)
10.某超市推出大米销售送货上门的业务,已知购买大米的总费用(含购买大米的费用+送货上门的费用)y(元)与购买大米的数量x(千克)满足一次函数关系,且当时,;当时,,若小王一次购买大米的总支出是254元,则他购买大米的数量为( )
A.48千克 B.49千克 C.50千克 D.51千克
二、填空题
11.如图,在平面直角坐标系中,已知直线,直线,直线交于点,交于点,过点作y轴的垂线交于点,过点作x轴的垂线,交于点,过点作y轴的垂线交于点,…,按此方式进行下去,则的坐标为 ,的坐标为 (用含n的式子表示,n为正整数).
12.乌鲁木齐至库尔勒的铁路长约600千米,火车从乌鲁木齐出发,其平均速度为110千米/时,则火车离库尔勒的距离s(千米)与行驶时间t(时)之间的函数关系式是 .
13.如图,已知A地在B地正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为 千米.
14.为响应国家号召,筑牢健康防线,重庆市民积极接种新冠疫苗,日前疫苗主要有三类:类(腺病毒载体疫苗)、类(灭活疫苗)、类(重组亚单位疫苗).甲、乙、丙三个接种点分别向市防疫站申请调拨了三类疫苗(其中每个接种点调拨的每一类疫苗剂数均为正整数),调拨一剂类疫苗的费用是调拨一剂类疫苗费用的3倍.甲接种点分别申请类80剂、类80剂、类40剂;丙接种点分别申请类80剂、类50剂、类80剂,丙调拨疫苗的总费用与甲的总费用相等.乙接种点申请的疫苗总数量比甲的总数量少20剂,其中类疫苗的剂数为9的整数倍,乙调拨的总费用不高于甲总费用的68.7%,但不低于甲总费用的68%.则乙接种点申请调拨类疫苗的最多数量是 剂.
15.已知,平面直角坐标系中,O为坐标原点,一次函数y=x+2的图象交x轴于点A,交y轴于点B,则的面积= .
16.平面直角坐标系中,点O为坐标原点,点A(4,2)、点B(0,5),直线y=kx﹣2k+1恰好将△ABO平均分成面积相等的两部分,则k的值是 .
17.在平面直角坐标系中,点的坐标分别为,,直线与线段有公共点,则的取值范围为 (用含的代数式表示).
18.如图,点是直线上的动点,过点作垂直轴于点,设点的坐标为,则点的坐标为 (用含的代数式表示),在轴上是否存在点,使为等腰直角三角形,请写出符合条件的点的坐标 .
19.直线与轴,轴分别交于A、B两点,若轴上有一点C,使得为等腰三角形的点C的坐标为 .
20.如图,在平面直角坐标系中,函数和的图象分别为直线,,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点,…,依次进行下去,则点的坐标为 ,点的坐标为 .
三、解答题
21.公交是一种绿色的出行方式,今年某县全面开通环保电动公交车.公交车在每天发车前需先将蓄电池充满,然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电量低于时,需停止运行.在充电和运行过程中,蓄电池的电量y(单位:)与时间(单位:h)之间的关系如图所示.已知当该电动公交车运行时,y与x的函数表达式为.
(1)该电动公交车每小时充电量为________;
(2)当该电动公交车运行时,求y关于x的函数表达式;
(3)当蓄电池的电量为时,求该电动公交车运行了多长时间?
22.郑州市政府为民生办实事,将污染多年的“贾鲁河”进行绿化改造,现需要购买大量的景观树.某苗木种植公司给出以下收费方案:
方案一:购买一张会员卡,所有购买的树苗按七折优惠;
方案二:不购买会员卡,所有购买的树苗按九折优惠.
设该市购买的景观树树苗棵数为x棵,方案一所需费用y1=k1x+b1,方案二所需费用y2=k2x,其函数图象如图所示,请根据图象回答下列问题.
(1)k1= ,b1= ;
(2)求每棵树苗的原价;
(3)求按照方案二购买所需费用的函数关系式y2=k2x,并说明k2的实际意义;
(4)若该市需要购买景观树600棵,采用哪种方案购买所需费用更少?请说明理由.
23.某超市分两次购进A、B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A商品以每件45元出售,B商品以每件75元出售.为满足市场需求,需购进A、B两种商品共1000件,且A商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并计算最大利润.
购进数量(件) 购进所需费用(元)
A B
第一次 30 40 2900
第二次 40 30 2700
24.为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1000米2的面积进行消杀.
(1)设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;
(2)在现有资金不超过5300元的情况下,求可消杀的最大面积.
25.某超市以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)当每千克干果降价3元时,超市获利多少元?
参考答案:
1.A
2.C
3.A
4.C
5.A
6.D
7.C
8.B
9.A
10.C
11.
12.
13.1.5/
14.126
15.4.
16.﹣2
17.m 6≤b≤m 4
18. ,,或
19.
20. (16,32) ( 21009, 21010).
21.(1)30
(2)
(3)
22.(1)21,3000;(2)每棵树苗的原价30元;(3)y2=27x,k2的实际意义是:每棵树苗打九折后的价格;(4)该市需要购买景观树600棵,采用方案一购买所需费用更少.
23.(1)A、B两种商品每件的进价分别是30元,50元;(2)A商品800件,B商品200件,最大利润为17000元.
24.(1)y=100x+4000(0<x<20且x为整数);(2)33000米2.
25.(1)y=10x+100(0<x<20);(2)当每千克干果降价3元时,超市获利2210元
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.4综合与实践一次函数模型的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行 2400 米,先到终点 的人原地休息.已知甲先出发 4 分钟,在整个步行过程中,甲、乙两人的距离 y(米)与 甲出发的时间 t(分)之间的关系如图所示,下列结论:①甲步行的速度为 60 米/分;②乙走完全程用了 34 分钟;③乙用 16 分钟追上甲;④乙到达终点时,甲离终点还有 300 米.其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4 个
2.如图,在正方形ABCD中,AB=a,E、F分别是AB、AD边上的点,BF,DE相交于点G,若AE=AB,AF=AD,则四边形BCDG的面积是( )
A. B. C. D.
3.一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则下列说法中:①每分钟进水5L;② 每分钟出水3.75L;③容器中水为25L的时间是8min或min;④第2或min时容器内的水恰为10升,错误的有( )
A.0个 B.1个 C.2个 D.3个
4.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为( )
A.140 B.138 C.148 D.160
5.公众号:武汉数学元朝朱世杰的《算学启蒙)一书记载:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”如图是良马与驽马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象,则两图象交点P的横坐标是( )
A.32 B.28 C.24 D.20
6.小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结账金额再减元.若小涵购买咖啡豆公克且自备容器,需支付元;阿嘉购买咖啡豆公克但没有自备容器,需支付元,则与的关系式为下列何者?( )
A. B.
C. D.
7.东东和爸爸一起往华中公园方向去旅游,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,东东继续前行,5分钟后也原路返回,两人恰好同时到家.东东和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论中错误的是( )
A.两人前行过程中的速度为200米/分
B.m的值是15,n的值是3000
C.东东开始返回时与爸爸相距1800米
D.运动18分钟或30分钟时,两人相距900米
8.如图,直线PA是一次函数的图象,直线PB是一次函数的图象,若PA与轴交于点Q,且,则的值分别是( )
A. B.2,1 C. D.
9.如图,直线y=﹣x+2与x轴.y轴分别交于A.B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( ).
A.(,3) B.(,) C.(2,2) D.(2,4)
10.某超市推出大米销售送货上门的业务,已知购买大米的总费用(含购买大米的费用+送货上门的费用)y(元)与购买大米的数量x(千克)满足一次函数关系,且当时,;当时,,若小王一次购买大米的总支出是254元,则他购买大米的数量为( )
A.48千克 B.49千克 C.50千克 D.51千克
二、填空题
11.如图,在平面直角坐标系中,已知直线,直线,直线交于点,交于点,过点作y轴的垂线交于点,过点作x轴的垂线,交于点,过点作y轴的垂线交于点,…,按此方式进行下去,则的坐标为 ,的坐标为 (用含n的式子表示,n为正整数).
12.乌鲁木齐至库尔勒的铁路长约600千米,火车从乌鲁木齐出发,其平均速度为110千米/时,则火车离库尔勒的距离s(千米)与行驶时间t(时)之间的函数关系式是 .
13.如图,已知A地在B地正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为 千米.
14.为响应国家号召,筑牢健康防线,重庆市民积极接种新冠疫苗,日前疫苗主要有三类:类(腺病毒载体疫苗)、类(灭活疫苗)、类(重组亚单位疫苗).甲、乙、丙三个接种点分别向市防疫站申请调拨了三类疫苗(其中每个接种点调拨的每一类疫苗剂数均为正整数),调拨一剂类疫苗的费用是调拨一剂类疫苗费用的3倍.甲接种点分别申请类80剂、类80剂、类40剂;丙接种点分别申请类80剂、类50剂、类80剂,丙调拨疫苗的总费用与甲的总费用相等.乙接种点申请的疫苗总数量比甲的总数量少20剂,其中类疫苗的剂数为9的整数倍,乙调拨的总费用不高于甲总费用的68.7%,但不低于甲总费用的68%.则乙接种点申请调拨类疫苗的最多数量是 剂.
15.已知,平面直角坐标系中,O为坐标原点,一次函数y=x+2的图象交x轴于点A,交y轴于点B,则的面积= .
16.平面直角坐标系中,点O为坐标原点,点A(4,2)、点B(0,5),直线y=kx﹣2k+1恰好将△ABO平均分成面积相等的两部分,则k的值是 .
17.在平面直角坐标系中,点的坐标分别为,,直线与线段有公共点,则的取值范围为 (用含的代数式表示).
18.如图,点是直线上的动点,过点作垂直轴于点,设点的坐标为,则点的坐标为 (用含的代数式表示),在轴上是否存在点,使为等腰直角三角形,请写出符合条件的点的坐标 .
19.直线与轴,轴分别交于A、B两点,若轴上有一点C,使得为等腰三角形的点C的坐标为 .
20.如图,在平面直角坐标系中,函数和的图象分别为直线,,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点,过点作轴的垂线交于点,…,依次进行下去,则点的坐标为 ,点的坐标为 .
三、解答题
21.公交是一种绿色的出行方式,今年某县全面开通环保电动公交车.公交车在每天发车前需先将蓄电池充满,然后立即开始不间断运行.为保障行车安全,当蓄电池剩余电量低于时,需停止运行.在充电和运行过程中,蓄电池的电量y(单位:)与时间(单位:h)之间的关系如图所示.已知当该电动公交车运行时,y与x的函数表达式为.
(1)该电动公交车每小时充电量为________;
(2)当该电动公交车运行时,求y关于x的函数表达式;
(3)当蓄电池的电量为时,求该电动公交车运行了多长时间?
22.郑州市政府为民生办实事,将污染多年的“贾鲁河”进行绿化改造,现需要购买大量的景观树.某苗木种植公司给出以下收费方案:
方案一:购买一张会员卡,所有购买的树苗按七折优惠;
方案二:不购买会员卡,所有购买的树苗按九折优惠.
设该市购买的景观树树苗棵数为x棵,方案一所需费用y1=k1x+b1,方案二所需费用y2=k2x,其函数图象如图所示,请根据图象回答下列问题.
(1)k1= ,b1= ;
(2)求每棵树苗的原价;
(3)求按照方案二购买所需费用的函数关系式y2=k2x,并说明k2的实际意义;
(4)若该市需要购买景观树600棵,采用哪种方案购买所需费用更少?请说明理由.
23.某超市分两次购进A、B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A商品以每件45元出售,B商品以每件75元出售.为满足市场需求,需购进A、B两种商品共1000件,且A商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并计算最大利润.
购进数量(件) 购进所需费用(元)
A B
第一次 30 40 2900
第二次 40 30 2700
24.为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1000米2的面积进行消杀.
(1)设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;
(2)在现有资金不超过5300元的情况下,求可消杀的最大面积.
25.某超市以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)当每千克干果降价3元时,超市获利多少元?
参考答案:
1.A
2.C
3.A
4.C
5.A
6.D
7.C
8.B
9.A
10.C
11.
12.
13.1.5/
14.126
15.4.
16.﹣2
17.m 6≤b≤m 4
18. ,,或
19.
20. (16,32) ( 21009, 21010).
21.(1)30
(2)
(3)
22.(1)21,3000;(2)每棵树苗的原价30元;(3)y2=27x,k2的实际意义是:每棵树苗打九折后的价格;(4)该市需要购买景观树600棵,采用方案一购买所需费用更少.
23.(1)A、B两种商品每件的进价分别是30元,50元;(2)A商品800件,B商品200件,最大利润为17000元.
24.(1)y=100x+4000(0<x<20且x为整数);(2)33000米2.
25.(1)y=10x+100(0<x<20);(2)当每千克干果降价3元时,超市获利2210元
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
