21.4 二次函数的应用分层练习(含答案)
文档属性
| 名称 | 21.4 二次函数的应用分层练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 06:35:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
21.4二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形ABCD是正方形,,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,的面积为y,则y关于x的函数图象大致为( )
A. B.
C. D.
2.某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度与水平距离之间的函数关系式是,则水池在喷水过程中水流的最大高度为( )
A.1.25米 B.2.25米 C.2.5米 D.3米
3.教练对小明推铅球的录像进行技术分析,发现铅球进行高度(单位:)与水平距离(单位:)之间的关系是,由此可知铅球能达到最大高度为( )
A. B.或 C. D.
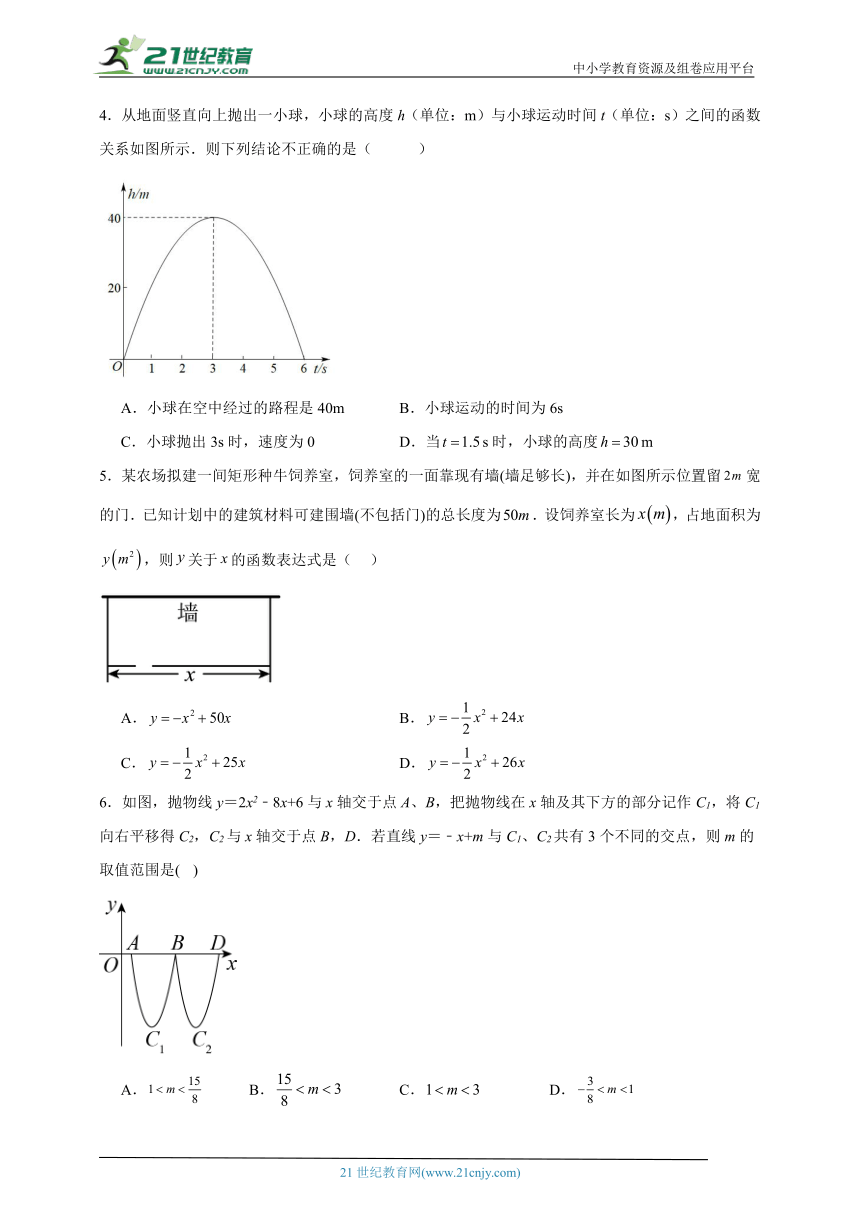
4.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
5.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留宽的门.已知计划中的建筑材料可建围墙(不包括门)的总长度为.设饲养室长为,占地面积为,则关于的函数表达式是( )
A. B.
C. D.
6.如图,抛物线y=2x2﹣8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=﹣x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
7.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是,飞机着陆至停下来共滑行( )
A.20米 B.40米 C.400米 D.600米
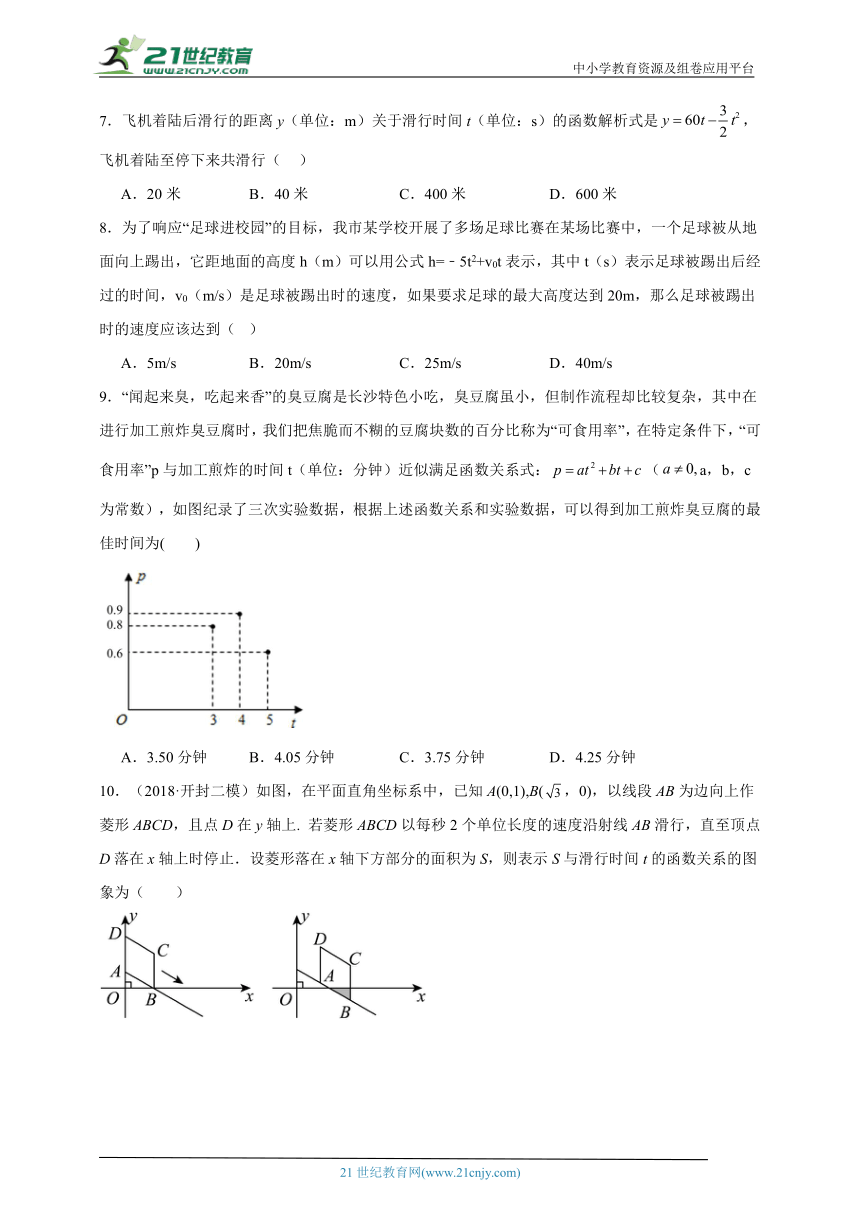
8.为了响应“足球进校园”的目标,我市某学校开展了多场足球比赛在某场比赛中,一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=﹣5t2+v0t表示,其中t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果要求足球的最大高度达到20m,那么足球被踢出时的速度应该达到( )
A.5m/s B.20m/s C.25m/s D.40m/s
9.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式:(a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
10.(2018·开封二模)如图,在平面直角坐标系中,已知A(0,1),B(,0),以线段AB为边向上作菱形ABCD,且点D在y轴上. 若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行,直至顶点D落在x轴上时停止.设菱形落在x轴下方部分的面积为S,则表示S与滑行时间t的函数关系的图象为( )
A. B. C. D.
二、填空题
11.某市民休闲广场中有一喷水设施,如图是喷水设施的一个喷头A喷出的水珠路线,它是一条经过A、M、C三点的抛物线.点A离地面1.4米,点M是路线的最高点,离地面3.2米,离喷头的水平距离为6米,点C是水珠落地点.那么水珠落地点C距喷头底部的水平距离为 米.
12.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.如果每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元,那么y与x的函数关系式是 .
13.从地面竖直向上抛出一个小球.小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是h=24t-4t2.小球运动的高度最大为 m.
14.如果关于x的二次函数y=2x2-3x+m与x轴只有一个交点,则m= .
15.汽车刹车后行驶的距离(单位:)与行驶的时间(单位:)之间的函数关系式是,当一辆行驶的汽车刹车后,在它的前方远的地方有一只小狗,那么这只小狗 出现危险(填“会”或者“不会”).
16.从地面竖直向上抛出一小球,小球的高度h(米)与小球运动时间t(秒)的关系式是h=30t﹣5t2,小球运动中的最大高度是 米.
17.用一段长为的篱笆围成一个一边靠墙的矩形养鸡场,若墙长,则这个养鸡场最大面积为 .
18.某杂技团用的幕布,围成一个长方形的临时场地,并在长的一边留出作为出口,设长方形的宽为,则该场地的面积与之间的函数关系式为 (化一般式).
19.如图是某同学正在设计的一个动画示意图,轴上依次有A,,三个点,且,在上方有五个台阶(各拐角均为),每个台阶的高、宽分别是1和,台阶到轴的距离.从点A处向右上方沿抛物线:发出一个带光的点.
(1)写出抛物线与轴的交点坐标为 ;
(2)的值为 ;
(3)通过计算可以说明点会落在台阶 上.
20.如图,一段抛物线记为,它与轴交于两点、,将绕旋转得到,交轴于,将绕旋转得到,交轴于;如此进行下去,直至得到,若点在第8段抛物线上,则等于
三、解答题
21.实验表明,汽车急刹车的停车距离等于反应距离与制动距离之和;反应距离与汽车速度成正比,制动距离与汽车速度的平方成正比.已知当汽车的速度为时,急刹车的停车距离为;当汽车的速度为时,急刹车的停车距离为.设汽车的速度为,急刹车的停车距离为.
(1)求关于的函数表达式;
(2)一辆汽车以的速度行驶,突然发现正前方处有一障碍物,紧急刹车,问汽车与障碍物是否会相撞?并说明理由;
(3)一辆行驶中的汽车突然发现正前方处有一辆抛锚的危险用品运输车,紧急刹车,要使汽车距离运输车不小于处停住,则汽车行驶的最大速度是__________.
22.某游乐场的圆形喷水池中心O有一喷水管OA,米,从A点向四周喷水,喷出的水柱为抛物线且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上.已知在与池中心O点水平距离为3米时,水柱达到最高,此时高度为2米.
(1)求水柱所在的抛物线(第一象限部分)的函数表达式;
(2)现重新改建喷泉,升高喷水管,使落水点与喷水管距离,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点处达到最高,则喷水管要升高多少?
23.如图,某校要用20m的篱笆,一面靠墙(墙长10m),围成一个矩形花圃,设矩形花圃垂直于墙的一边长为xm,花圃的面积为ym2.
(1)求出y与x的函数关系式.
(2)当矩形花圃的面积为48m2时,求x的值.
(3)当边长x为多少时,矩形的面积最大,最大面积是多少
24.某公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 30 35 40 45 50
日销售量p(千克) 600 450 300 150 0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)该公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若该公司的日销售利润不低于2250元,应该如何确定销售价格?
25.“健行”保健器械厂在某社区举办“品牌跑步机团购销售”活动,销售规则如下:若团购台数在台或台以下,跑步机每台售价元;若团购台数多于台,则给予优惠,每多台,跑步机每台少元,但团购台数最多为台,已知器械厂举办该次活动须支付各项成本元.那么当团购台数为多少时,器械厂可获得的利润最大?是多少元?
参考答案:
1.A
2.B
3.D
4.A
5.D
6.B
7.D
8.B
9.C
10.A
11.14
12.
13.36
14.
15.不会
16.45
17.64
18.
19. 4
20.
21.(1)
(2)会相撞
(3)30
22.(1)
(2)m
23.(1)y= 2x2+20x;(2)6;(3)x=5时,y最大值=50.
24.(1);(2)40元;(3)35元
25.当团购台数为台时,器械厂可获得最大利润为元
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
21.4二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形ABCD是正方形,,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,的面积为y,则y关于x的函数图象大致为( )
A. B.
C. D.
2.某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度与水平距离之间的函数关系式是,则水池在喷水过程中水流的最大高度为( )
A.1.25米 B.2.25米 C.2.5米 D.3米
3.教练对小明推铅球的录像进行技术分析,发现铅球进行高度(单位:)与水平距离(单位:)之间的关系是,由此可知铅球能达到最大高度为( )
A. B.或 C. D.
4.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
5.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留宽的门.已知计划中的建筑材料可建围墙(不包括门)的总长度为.设饲养室长为,占地面积为,则关于的函数表达式是( )
A. B.
C. D.
6.如图,抛物线y=2x2﹣8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=﹣x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
7.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是,飞机着陆至停下来共滑行( )
A.20米 B.40米 C.400米 D.600米
8.为了响应“足球进校园”的目标,我市某学校开展了多场足球比赛在某场比赛中,一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=﹣5t2+v0t表示,其中t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果要求足球的最大高度达到20m,那么足球被踢出时的速度应该达到( )
A.5m/s B.20m/s C.25m/s D.40m/s
9.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式:(a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
10.(2018·开封二模)如图,在平面直角坐标系中,已知A(0,1),B(,0),以线段AB为边向上作菱形ABCD,且点D在y轴上. 若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行,直至顶点D落在x轴上时停止.设菱形落在x轴下方部分的面积为S,则表示S与滑行时间t的函数关系的图象为( )
A. B. C. D.
二、填空题
11.某市民休闲广场中有一喷水设施,如图是喷水设施的一个喷头A喷出的水珠路线,它是一条经过A、M、C三点的抛物线.点A离地面1.4米,点M是路线的最高点,离地面3.2米,离喷头的水平距离为6米,点C是水珠落地点.那么水珠落地点C距喷头底部的水平距离为 米.
12.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.如果每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元,那么y与x的函数关系式是 .
13.从地面竖直向上抛出一个小球.小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是h=24t-4t2.小球运动的高度最大为 m.
14.如果关于x的二次函数y=2x2-3x+m与x轴只有一个交点,则m= .
15.汽车刹车后行驶的距离(单位:)与行驶的时间(单位:)之间的函数关系式是,当一辆行驶的汽车刹车后,在它的前方远的地方有一只小狗,那么这只小狗 出现危险(填“会”或者“不会”).
16.从地面竖直向上抛出一小球,小球的高度h(米)与小球运动时间t(秒)的关系式是h=30t﹣5t2,小球运动中的最大高度是 米.
17.用一段长为的篱笆围成一个一边靠墙的矩形养鸡场,若墙长,则这个养鸡场最大面积为 .
18.某杂技团用的幕布,围成一个长方形的临时场地,并在长的一边留出作为出口,设长方形的宽为,则该场地的面积与之间的函数关系式为 (化一般式).
19.如图是某同学正在设计的一个动画示意图,轴上依次有A,,三个点,且,在上方有五个台阶(各拐角均为),每个台阶的高、宽分别是1和,台阶到轴的距离.从点A处向右上方沿抛物线:发出一个带光的点.
(1)写出抛物线与轴的交点坐标为 ;
(2)的值为 ;
(3)通过计算可以说明点会落在台阶 上.
20.如图,一段抛物线记为,它与轴交于两点、,将绕旋转得到,交轴于,将绕旋转得到,交轴于;如此进行下去,直至得到,若点在第8段抛物线上,则等于
三、解答题
21.实验表明,汽车急刹车的停车距离等于反应距离与制动距离之和;反应距离与汽车速度成正比,制动距离与汽车速度的平方成正比.已知当汽车的速度为时,急刹车的停车距离为;当汽车的速度为时,急刹车的停车距离为.设汽车的速度为,急刹车的停车距离为.
(1)求关于的函数表达式;
(2)一辆汽车以的速度行驶,突然发现正前方处有一障碍物,紧急刹车,问汽车与障碍物是否会相撞?并说明理由;
(3)一辆行驶中的汽车突然发现正前方处有一辆抛锚的危险用品运输车,紧急刹车,要使汽车距离运输车不小于处停住,则汽车行驶的最大速度是__________.
22.某游乐场的圆形喷水池中心O有一喷水管OA,米,从A点向四周喷水,喷出的水柱为抛物线且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上.已知在与池中心O点水平距离为3米时,水柱达到最高,此时高度为2米.
(1)求水柱所在的抛物线(第一象限部分)的函数表达式;
(2)现重新改建喷泉,升高喷水管,使落水点与喷水管距离,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点处达到最高,则喷水管要升高多少?
23.如图,某校要用20m的篱笆,一面靠墙(墙长10m),围成一个矩形花圃,设矩形花圃垂直于墙的一边长为xm,花圃的面积为ym2.
(1)求出y与x的函数关系式.
(2)当矩形花圃的面积为48m2时,求x的值.
(3)当边长x为多少时,矩形的面积最大,最大面积是多少
24.某公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 30 35 40 45 50
日销售量p(千克) 600 450 300 150 0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)该公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若该公司的日销售利润不低于2250元,应该如何确定销售价格?
25.“健行”保健器械厂在某社区举办“品牌跑步机团购销售”活动,销售规则如下:若团购台数在台或台以下,跑步机每台售价元;若团购台数多于台,则给予优惠,每多台,跑步机每台少元,但团购台数最多为台,已知器械厂举办该次活动须支付各项成本元.那么当团购台数为多少时,器械厂可获得的利润最大?是多少元?
参考答案:
1.A
2.B
3.D
4.A
5.D
6.B
7.D
8.B
9.C
10.A
11.14
12.
13.36
14.
15.不会
16.45
17.64
18.
19. 4
20.
21.(1)
(2)会相撞
(3)30
22.(1)
(2)m
23.(1)y= 2x2+20x;(2)6;(3)x=5时,y最大值=50.
24.(1);(2)40元;(3)35元
25.当团购台数为台时,器械厂可获得最大利润为元
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
