平方根1

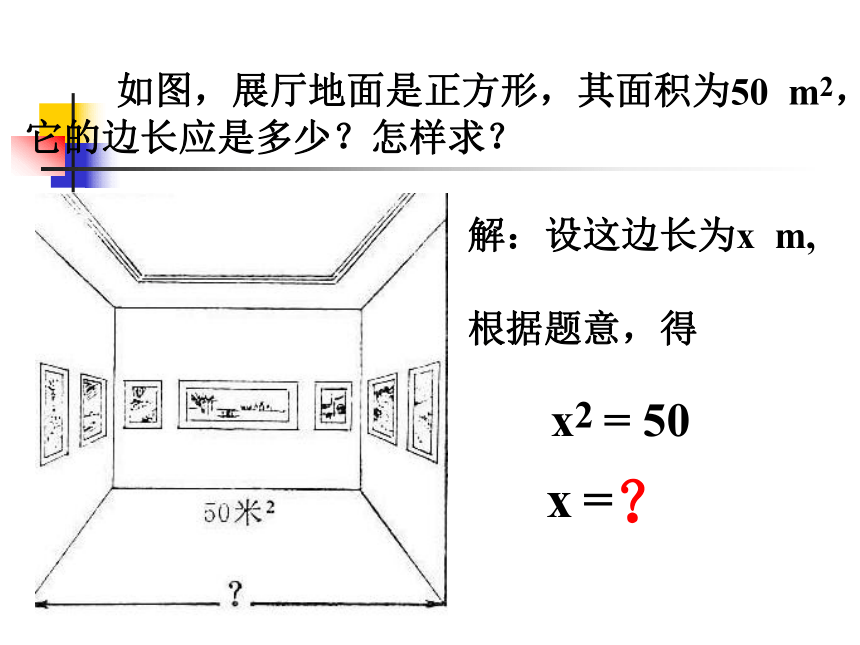
课件19张PPT。引子平方根（一）如图，一正方形边长10cm，求它的面积。10cm 如图，展厅地面是正方形，其面积为50 m2，它的边长应是多少？怎样求？解：设这边长为x m,根据题意，得x2 = 50x =？一个数的平方是 9，这个数是什么数？解：∵ 3 2 = 9，( - 3 ) 2 = 9∴这个数是 3 或 –3 。思考题：一个数的平方是 ，这个数是什么数？∴这个数是 或 – 。思考题：解：∵( ) 2 = ，( - ) 2 = 一般地，如果一个数的平方等于a，这个数就叫做a的平方根（或二次方根）。就是说:如果x2=a，那么x叫做a的平方根。定义：一个正数有两个平方根，它们互为相反数；性 质0有一个平方根，它是0本身；负数没有平方根。1、因为（0.3）2=0.09 所以（ ）
A、0.09是0.3的平方根；B、0.09是0.3的3倍；
C、0.3是0.09的平方根；D、0.3不是0.09的平方根2、判断下列各数有没有平方根？有几个？
49 0 - 42 （ ）2 练 习2读作 二次根号a2读作 正负根号a(a≥0)1、25的平方根是±5，这句话用数学式子表示为（ ）
A、 25=±5；B、± 25=±5；C、 25=5；
D、- 25=-5练习2、判断：
（1 ） 0的平方根是0； （ ）
（2）1的平方根是1； （ ）
（3） -1 = -1 （ ）
（4） 16=±4； （ ）
（5）若x2=16，则x= 16=4； （ ）
（6） (-9)2=-9 （ ）
B求一个数的平方根的运算叫做开平方。定义：例1：求下列各数的平方根：
（1）81；（2） ；（3）2 ；（4）0.49 解：(1) ∵(±9)2=81 ∴81的平方根是±9；即± 81 = ±9 例2：下列各数有平方根吗？如果有，求出它的平方根，如果没有，说明理由。
(1)-64 (2) 0 (3) (-4)2 (4) 10-21、检验下面各题中前面的数是不是后面数的平方根：
（1）±12，144； （2）±0.2，0.04；
（3）102，104； （4）14，256。2、如图，求左圈和右圈中的“？”表示的数：练 习定义：求一个数的平方根的运算，叫做开平方。小 结当a=0时，a的平方根是0。 1、对于代数式3m-9，当m取何值时，（1）有两个平方根，并且它们互为相反数？（2）只有一个平方根？（3）没有平方根？
2、√x-2 是 x-2 的平方根,则x
3、一个正数的正的平方根是m，那么比这个正数大1的数的平方根是（ ）
A、m2+1；B、±√m+1；C、√m2+1；
D、±√m2+1思考题：