研究中考试题的几个视角(以2014年安徽中考试卷为例)2015.3.27
文档属性
| 名称 | 研究中考试题的几个视角(以2014年安徽中考试卷为例)2015.3.27 |

|
|
| 格式 | zip | ||
| 文件大小 | 454.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-08 00:00:00 | ||
图片预览








文档简介
课件40张PPT。研究中考试题的几个视角阜阳市教育科学研究所
王志刚
2015年3月命题者的思想
知识点的分布(与历年试题的重合度)
能力层次
与教材的关联度
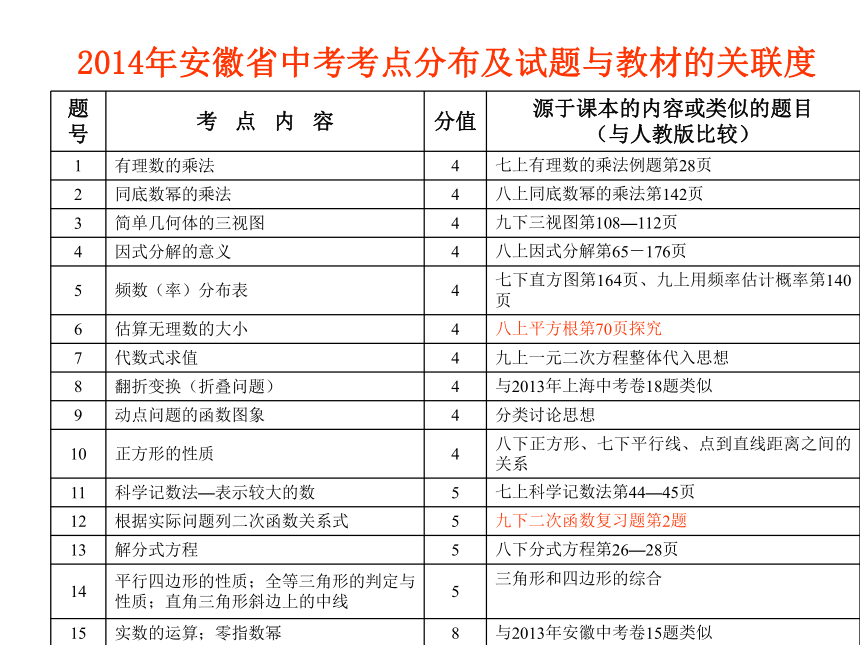
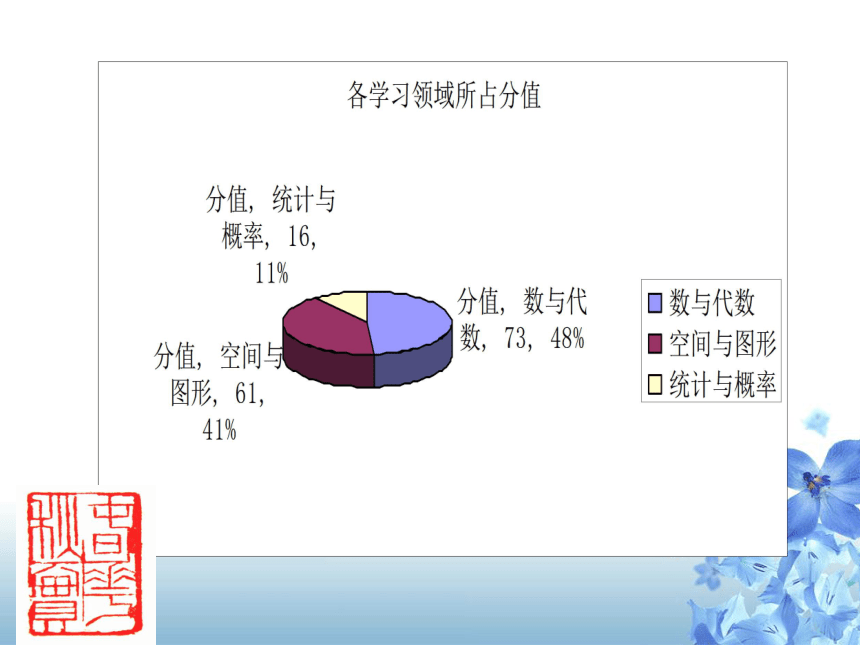
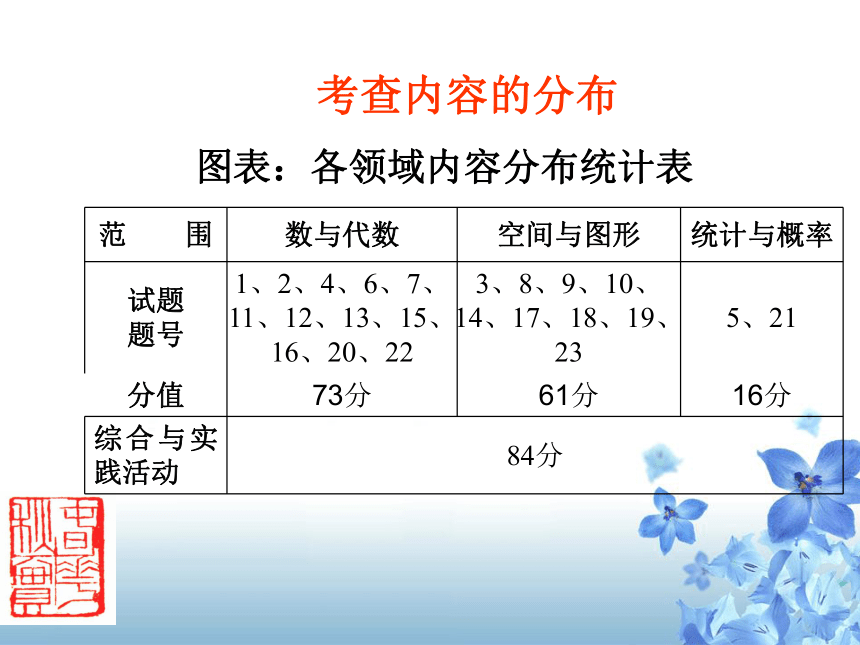
整卷的难度一、认真研究试题的双向细目表设计双向细目表是命题工作的第一步2014年安徽省中考考点分布及试题与教材的关联度观点一方面,每年的中考试题都在往年的基础上设置有一定的继承性,但也有所突破,适应了课改稳中求变,变中求新的趋势,另一方面,对全国各地中考试题的精品试题有所借鉴。只要潜心钻研,往往可以发现安徽中考试题的一些规律与演化的轨迹。图表:各领域内容分布统计表 考查内容的分布试题涉及七、八、九三个年级所学内容,以九年级所学知识为主体。
七年级占35分,主要是有理数的乘法、直方图、用坐标表示平移、二元一次方程组等。
八年级占35分,主要是同底数幂的乘法、因式分解、平方根、分式方程、全等三角形、四边形等。
其余为九年级内容,九年级内容占80分。
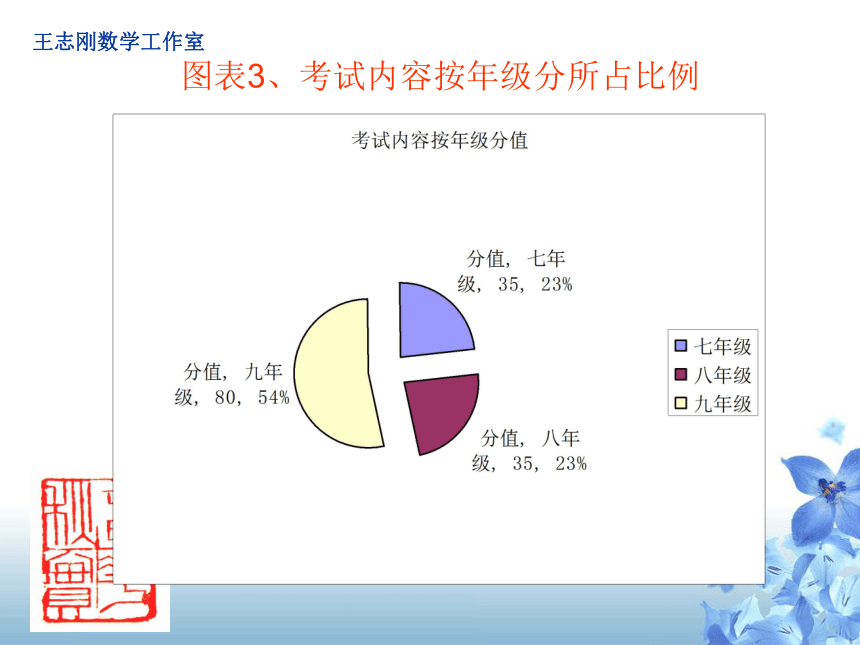
部分试题的原型来自课本和《考试纲要》,并对其进行了适当的改编与整合,赋之以新的情境,新的形式和新的材料。考试内容按年级分年级所占比例图表3、考试内容按年级分所占比例王志刚数学工作室二、研究试题的解答思路一般来说,中考考试卷中的很多试题是不止一种解法的,有繁简之别,数学素养好的考生因为思维有深度,能透过现象看到本质,在面对同一道试题,能机智地选择出一种最佳的解决方案,而数学素养不高的考生,只能按部就班地解答,虽然也能解答出来,但费时费力,解题速度慢。 值得注意研究试题的解法人人都能做,但如果只停留就方法展示的层面上,意义不大,因为研究中考试题解法思路的目的是透视命题者命题的心路历程,不是为多解而多解,而是为了解决一类问题的求解方案,达到学一题会一类的目的,故我们在研究中考试题的多种解法思路之后,要进行对比归纳,提炼解题规律,使学生在今后当拿到此类问题时,能够快速形成解题方案。【题例】10.(4分)(2014?安徽)如图,正方形ABCD的对角线BD长为 ,若直线l满足:
①点D到直线l的距离为 ;
②A、C两点到直线l的距离相等.则符合题意的直线l的条数为( )
A.1 B.2 C.3 D.4 该题的考查知识点有:点到直线距离的定义、正方形的对称性、点的轨迹、圆的相关知识、无理数的估计等。
该题有很好的衔接性和综合性,作为选择题的压轴题,确实是难得优秀的中考试题。??解法一:首先直线l满足①,即直线l到D的距离为3,那么点D到直线l的垂线垂足的轨迹,即位于以点D为圆心,3为半径的圆上(图10-1),这一步有相当衔接性,以及对数学素养的较高要求。其次直线l满足②?,即直线l到A、C两点距离相等,直观感觉,倘若直线l与BD所在直线重合,必然有直线l到A、C两点距离相等。如图所示,连接AC后看得更清楚,AC与BD交于点O。由此想到直线l过对正方形称中心点O(图10-2)或 平行于AC(图10-3)。如图所示,这一步很多考生由于缺乏数感,随手画图,没有发现点O在圆的内部导致增解,容易选D。
?继续研讨,平行于AC的直线l满足条件②?有两条直线,如图所示。?所以B是正确答案。?解法二:也可以让直线l先满足②,已知l平行于直线AC或过正方形称中心点O。如图
(图10-4)直线l∥AC并且到D的距离为,同理,在点D的另一侧还有一条直线满足条件;(图10-4)再根据正方形的性质求出OD= ,若l过正方形称中心点O,则D到直线l的距离小于,
故共有2条直线l。14.(5分)(2014?安徽)如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上)
①∠DCF=∠BCD
②EF=CF;
③S△BEC=2S△CEF;
④∠DFE=3∠AEF.评析:此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,几何直观能力。解法一:(如图14-1)分别利用平行四边形的性质以及全等三角形的判定
与性质得出△AEF≌△DMF,得出对应线段之间关系进而得出答案 如图14-1④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°﹣x,∴∠EFC=180°﹣2x,∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,HG图14-2
∵∠AEF=90°﹣x,∴∠DFE=3∠AEF,故此选项正确.解法二:(如图14-2)理由同上①选项正确。
②过F作FG∥BE交BC于G,则由题意知FG⊥EC于H,G为BC中点,所以H也为EC中点,即FG垂直平分EC,因此FC=FM,故②正确;
由②得BE=2HG,而FG≠HG,故S△BEC=2S△CEF错误。
④∵FG∥BE ∴∠AEF=∠EFG,由①得四边形FGCD为菱形,所以∠GFC=∠DFC; 由②得∠EFG =∠GFC,
∴∠DFE=3∠AEF,故答案为:①②④.GH几何感知(1)度量法。
(2)排除法,很明显③是错的,依据以往经验答案往往是3个,从而得到答案。
(3)推理法。如果②对能推出④也对,依据第二种想法,很明显③是错的, 阜南赵集中心校韦立玲二次函数的解析式的求法
(一)自主学习
(二)合作探究
根据下列条件求抛物线的解析式
1、抛物线过点(0,0) (1,2) (2,3)三点;
2、抛物线的顶点坐标是(2,-1)且过点(-1,2);
3、图像与x轴交于(2,0) (-1,0),且过点(0,-2).怎样分析解题思路?题量大就是容量大吗?19.(10分)(2014?安徽)如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.三、访谈探索学生学习答题心理3.如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是【 】考的是关于视图问题,在小学时已多次接触。
王正阳(九(24)班,中考数学得分140.5分)
这是容易题,由于粗心作错了。(肖亚杰(九(24)班,中考成绩76分)9.如图,在矩形ABCD中,,动点从点出发,按的方向在和上移动。记,点到的距离为,则关于的函数图像大致是....【 】平时见此类问题就常常做错,(老师)每次讲解只是半懂,在中考复习时也是因为只为了其他题目的正确因为疏忽了此类问题,从而做错。 (肖亚杰(九(24)班,中考成绩76分)
有一定难度,考了几何(与)函数图像的结合,加入了分段函数。但结果很容易看出来,可以蒙对。王正阳(九(24)班,中考数学得分140.5分)
10.如图,正方形的对角线长为 ,若直线满足:①点到直线的距离为 ;②两点到直线的距离相等。则符合题意的直线的条数为....................【 】
A 1 . B.2
C.3 . D.4
图形问题,做辅助线此类问题我是可以做,但是在规则图形上此类问题我是没有解决办法。(肖亚杰(九(24)班,中考成绩76分)
有一定难度,考的知识不难,当时技巧性强,很难答全,方法是用圆规取(值)后画圆看出答案。王正阳(九(24)班,中考数学得分140.5分)
14.如图,在中,,是的中点,作,垂足在线段上,连接,则下列结论中一定成立的是___________.(把所有正确结论的序号都填在横线上).
①
②
③
④考的是几何问题,难度很大,很难答全,但是因为画图比较准确,可以通过测量得出答案,几何知识考的比较综合,单靠知识解决十分困难。干脆放弃!节省时间。(王正阳(九(24)班,中考数学得分140.5分)
此类问题解决的时候不是缺一个就是多一个,每次做的时候要经过长时间的推理,很烦。要掌握大量数学知识。胡乱写三个。肖亚杰(九(24)班,中考成绩76分)12.某厂今年一月份新产品的研发资金为元,以后每月新产品的研发资金与上月相比增长率都是,则该厂今年三月份新产品的研发资金(元)关于的函数关系式为________.
此类问题的解答我是半懂,在考场上没有打草稿,只是凭着自己看得着的结论,是由于自己的失误。(肖亚杰(九(24)班,中考成绩76分)王正阳(九(24)班,中考数学得分140.5分)第3题:考的是关于视图问题,在小学时已多次接触。
第7题:考的是整体代入思想,答案为6,却有6或-2这一干扰选项,虚心易答错。
第9题:有一定难度,考了几何(与)函数图像的结合,加入了分段函数。但结果很容易看出来,可以蒙对。
第10题:有一定难度,考的知识不难,当时技巧性强,很难答全,方法是用圆规取(值)后画圆看出答案。
第14题:考的是几何问题,难度很大,很难答全,但是因为画图比较准确,可以通过测量得出答案,几何知识考的比较综合,单靠知识解决十分困难。
第23题:是唯一错的题目,难度很大,大部分人都没有答对。考纲中说明补考梯形,此题却用两个梯形组成六边形。难度很大,辅助线很难添加,对知识(要)思想要求很高。但本人也有失误之处,在学科知识方面基础薄弱,故做不出此题,但心服口服。
1.重视培养学生的审题能力。现今很多学校学生作业较多,而学生做作业的首要目标是完成任务,导致学生“快餐式练习”,不得不削弱审题时间,容易出现一些无谓失误。比如选择题第3题正确答案为D,学生容易选A;第20题中垃圾处理费8800元是比上一年多支出的费用,考生容易理解为这就是2014年垃圾处理费等。
2.重视培养学生的计算能力。今年试题总体计算量较大。比如第18题、第20题、第22题均要求学生有一定的计算能力,否则思路正确不一定能得分。
3.重视培养学生提出问题、分析问题和解决问题的能力。历年来安徽中考数学试题大部分题均为原创,学生均感觉较为陌生,平时只有多从提高数学思维能力上些功夫,才能以不变应万变。想法四、研究典型考题的题根 每年中考都会引发一线教师的关注和思考,特别是一些把关题,更是教师研究的重点,既然是把关题,到底是怎样把关的?学生思维受阻的根源在哪里?是题目新颖导致的吗?还是其它原因。
不少中考把关题乍一看,题面崭新,但通过研究发现之前中考也考过类似的问题,其实大家认为类似的问题就是指当年的考题与往年试卷中的某个题有相同的地方,即都含有同一个问题,这就是我们通常说的“题根”,如果某个题根比较抽象,学生不易理解掌握,则这个“题根”就越受中考专家的青睐。 对第23题的思考23.(14分)(2014?安徽)如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= 60° ;
②求证:PM+PN=3a;
(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.等腰梯形内接菱形的若干特征五、得分情况分析(三个不同的结果)统计人数19024人图表5:试题的各项系数(看难度系数)
大规模19024人庞丽丽抽样数据得分率折线图做到一种思路:知己知彼,百战不殆。
一个导向:知识与方法兼顾,能力培养与情感教育统筹。
一种模式:精解考题,深析知识点,点拨答题技巧,研究中考趋势,预测命题方向。
一个目标:轻松备战,有效收获,赢在中考。谢 谢!
王志刚
2015年3月命题者的思想
知识点的分布(与历年试题的重合度)
能力层次
与教材的关联度
整卷的难度一、认真研究试题的双向细目表设计双向细目表是命题工作的第一步2014年安徽省中考考点分布及试题与教材的关联度观点一方面,每年的中考试题都在往年的基础上设置有一定的继承性,但也有所突破,适应了课改稳中求变,变中求新的趋势,另一方面,对全国各地中考试题的精品试题有所借鉴。只要潜心钻研,往往可以发现安徽中考试题的一些规律与演化的轨迹。图表:各领域内容分布统计表 考查内容的分布试题涉及七、八、九三个年级所学内容,以九年级所学知识为主体。
七年级占35分,主要是有理数的乘法、直方图、用坐标表示平移、二元一次方程组等。
八年级占35分,主要是同底数幂的乘法、因式分解、平方根、分式方程、全等三角形、四边形等。
其余为九年级内容,九年级内容占80分。
部分试题的原型来自课本和《考试纲要》,并对其进行了适当的改编与整合,赋之以新的情境,新的形式和新的材料。考试内容按年级分年级所占比例图表3、考试内容按年级分所占比例王志刚数学工作室二、研究试题的解答思路一般来说,中考考试卷中的很多试题是不止一种解法的,有繁简之别,数学素养好的考生因为思维有深度,能透过现象看到本质,在面对同一道试题,能机智地选择出一种最佳的解决方案,而数学素养不高的考生,只能按部就班地解答,虽然也能解答出来,但费时费力,解题速度慢。 值得注意研究试题的解法人人都能做,但如果只停留就方法展示的层面上,意义不大,因为研究中考试题解法思路的目的是透视命题者命题的心路历程,不是为多解而多解,而是为了解决一类问题的求解方案,达到学一题会一类的目的,故我们在研究中考试题的多种解法思路之后,要进行对比归纳,提炼解题规律,使学生在今后当拿到此类问题时,能够快速形成解题方案。【题例】10.(4分)(2014?安徽)如图,正方形ABCD的对角线BD长为 ,若直线l满足:
①点D到直线l的距离为 ;
②A、C两点到直线l的距离相等.则符合题意的直线l的条数为( )
A.1 B.2 C.3 D.4 该题的考查知识点有:点到直线距离的定义、正方形的对称性、点的轨迹、圆的相关知识、无理数的估计等。
该题有很好的衔接性和综合性,作为选择题的压轴题,确实是难得优秀的中考试题。??解法一:首先直线l满足①,即直线l到D的距离为3,那么点D到直线l的垂线垂足的轨迹,即位于以点D为圆心,3为半径的圆上(图10-1),这一步有相当衔接性,以及对数学素养的较高要求。其次直线l满足②?,即直线l到A、C两点距离相等,直观感觉,倘若直线l与BD所在直线重合,必然有直线l到A、C两点距离相等。如图所示,连接AC后看得更清楚,AC与BD交于点O。由此想到直线l过对正方形称中心点O(图10-2)或 平行于AC(图10-3)。如图所示,这一步很多考生由于缺乏数感,随手画图,没有发现点O在圆的内部导致增解,容易选D。
?继续研讨,平行于AC的直线l满足条件②?有两条直线,如图所示。?所以B是正确答案。?解法二:也可以让直线l先满足②,已知l平行于直线AC或过正方形称中心点O。如图
(图10-4)直线l∥AC并且到D的距离为,同理,在点D的另一侧还有一条直线满足条件;(图10-4)再根据正方形的性质求出OD= ,若l过正方形称中心点O,则D到直线l的距离小于,
故共有2条直线l。14.(5分)(2014?安徽)如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上)
①∠DCF=∠BCD
②EF=CF;
③S△BEC=2S△CEF;
④∠DFE=3∠AEF.评析:此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,几何直观能力。解法一:(如图14-1)分别利用平行四边形的性质以及全等三角形的判定
与性质得出△AEF≌△DMF,得出对应线段之间关系进而得出答案 如图14-1④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°﹣x,∴∠EFC=180°﹣2x,∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,HG图14-2
∵∠AEF=90°﹣x,∴∠DFE=3∠AEF,故此选项正确.解法二:(如图14-2)理由同上①选项正确。
②过F作FG∥BE交BC于G,则由题意知FG⊥EC于H,G为BC中点,所以H也为EC中点,即FG垂直平分EC,因此FC=FM,故②正确;
由②得BE=2HG,而FG≠HG,故S△BEC=2S△CEF错误。
④∵FG∥BE ∴∠AEF=∠EFG,由①得四边形FGCD为菱形,所以∠GFC=∠DFC; 由②得∠EFG =∠GFC,
∴∠DFE=3∠AEF,故答案为:①②④.GH几何感知(1)度量法。
(2)排除法,很明显③是错的,依据以往经验答案往往是3个,从而得到答案。
(3)推理法。如果②对能推出④也对,依据第二种想法,很明显③是错的, 阜南赵集中心校韦立玲二次函数的解析式的求法
(一)自主学习
(二)合作探究
根据下列条件求抛物线的解析式
1、抛物线过点(0,0) (1,2) (2,3)三点;
2、抛物线的顶点坐标是(2,-1)且过点(-1,2);
3、图像与x轴交于(2,0) (-1,0),且过点(0,-2).怎样分析解题思路?题量大就是容量大吗?19.(10分)(2014?安徽)如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.三、访谈探索学生学习答题心理3.如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是【 】考的是关于视图问题,在小学时已多次接触。
王正阳(九(24)班,中考数学得分140.5分)
这是容易题,由于粗心作错了。(肖亚杰(九(24)班,中考成绩76分)9.如图,在矩形ABCD中,,动点从点出发,按的方向在和上移动。记,点到的距离为,则关于的函数图像大致是....【 】平时见此类问题就常常做错,(老师)每次讲解只是半懂,在中考复习时也是因为只为了其他题目的正确因为疏忽了此类问题,从而做错。 (肖亚杰(九(24)班,中考成绩76分)
有一定难度,考了几何(与)函数图像的结合,加入了分段函数。但结果很容易看出来,可以蒙对。王正阳(九(24)班,中考数学得分140.5分)
10.如图,正方形的对角线长为 ,若直线满足:①点到直线的距离为 ;②两点到直线的距离相等。则符合题意的直线的条数为....................【 】
A 1 . B.2
C.3 . D.4
图形问题,做辅助线此类问题我是可以做,但是在规则图形上此类问题我是没有解决办法。(肖亚杰(九(24)班,中考成绩76分)
有一定难度,考的知识不难,当时技巧性强,很难答全,方法是用圆规取(值)后画圆看出答案。王正阳(九(24)班,中考数学得分140.5分)
14.如图,在中,,是的中点,作,垂足在线段上,连接,则下列结论中一定成立的是___________.(把所有正确结论的序号都填在横线上).
①
②
③
④考的是几何问题,难度很大,很难答全,但是因为画图比较准确,可以通过测量得出答案,几何知识考的比较综合,单靠知识解决十分困难。干脆放弃!节省时间。(王正阳(九(24)班,中考数学得分140.5分)
此类问题解决的时候不是缺一个就是多一个,每次做的时候要经过长时间的推理,很烦。要掌握大量数学知识。胡乱写三个。肖亚杰(九(24)班,中考成绩76分)12.某厂今年一月份新产品的研发资金为元,以后每月新产品的研发资金与上月相比增长率都是,则该厂今年三月份新产品的研发资金(元)关于的函数关系式为________.
此类问题的解答我是半懂,在考场上没有打草稿,只是凭着自己看得着的结论,是由于自己的失误。(肖亚杰(九(24)班,中考成绩76分)王正阳(九(24)班,中考数学得分140.5分)第3题:考的是关于视图问题,在小学时已多次接触。
第7题:考的是整体代入思想,答案为6,却有6或-2这一干扰选项,虚心易答错。
第9题:有一定难度,考了几何(与)函数图像的结合,加入了分段函数。但结果很容易看出来,可以蒙对。
第10题:有一定难度,考的知识不难,当时技巧性强,很难答全,方法是用圆规取(值)后画圆看出答案。
第14题:考的是几何问题,难度很大,很难答全,但是因为画图比较准确,可以通过测量得出答案,几何知识考的比较综合,单靠知识解决十分困难。
第23题:是唯一错的题目,难度很大,大部分人都没有答对。考纲中说明补考梯形,此题却用两个梯形组成六边形。难度很大,辅助线很难添加,对知识(要)思想要求很高。但本人也有失误之处,在学科知识方面基础薄弱,故做不出此题,但心服口服。
1.重视培养学生的审题能力。现今很多学校学生作业较多,而学生做作业的首要目标是完成任务,导致学生“快餐式练习”,不得不削弱审题时间,容易出现一些无谓失误。比如选择题第3题正确答案为D,学生容易选A;第20题中垃圾处理费8800元是比上一年多支出的费用,考生容易理解为这就是2014年垃圾处理费等。
2.重视培养学生的计算能力。今年试题总体计算量较大。比如第18题、第20题、第22题均要求学生有一定的计算能力,否则思路正确不一定能得分。
3.重视培养学生提出问题、分析问题和解决问题的能力。历年来安徽中考数学试题大部分题均为原创,学生均感觉较为陌生,平时只有多从提高数学思维能力上些功夫,才能以不变应万变。想法四、研究典型考题的题根 每年中考都会引发一线教师的关注和思考,特别是一些把关题,更是教师研究的重点,既然是把关题,到底是怎样把关的?学生思维受阻的根源在哪里?是题目新颖导致的吗?还是其它原因。
不少中考把关题乍一看,题面崭新,但通过研究发现之前中考也考过类似的问题,其实大家认为类似的问题就是指当年的考题与往年试卷中的某个题有相同的地方,即都含有同一个问题,这就是我们通常说的“题根”,如果某个题根比较抽象,学生不易理解掌握,则这个“题根”就越受中考专家的青睐。 对第23题的思考23.(14分)(2014?安徽)如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= 60° ;
②求证:PM+PN=3a;
(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.等腰梯形内接菱形的若干特征五、得分情况分析(三个不同的结果)统计人数19024人图表5:试题的各项系数(看难度系数)
大规模19024人庞丽丽抽样数据得分率折线图做到一种思路:知己知彼,百战不殆。
一个导向:知识与方法兼顾,能力培养与情感教育统筹。
一种模式:精解考题,深析知识点,点拨答题技巧,研究中考趋势,预测命题方向。
一个目标:轻松备战,有效收获,赢在中考。谢 谢!
同课章节目录
