5.1.2垂线
图片预览





文档简介
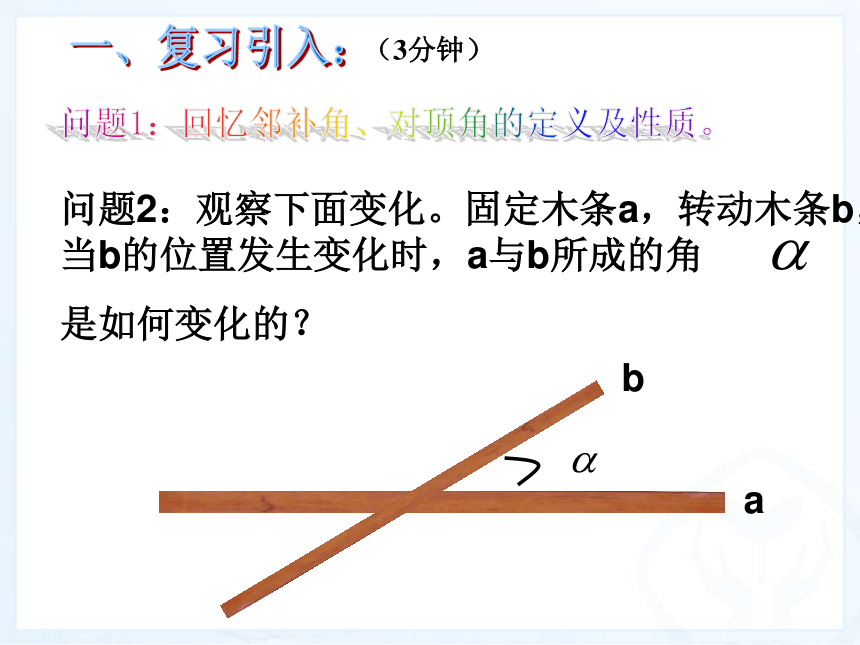
课件41张PPT。5.1.2 垂线问题2:观察下面变化。固定木条a,转动木条b,当b的位置发生变化时,a与b所成的角
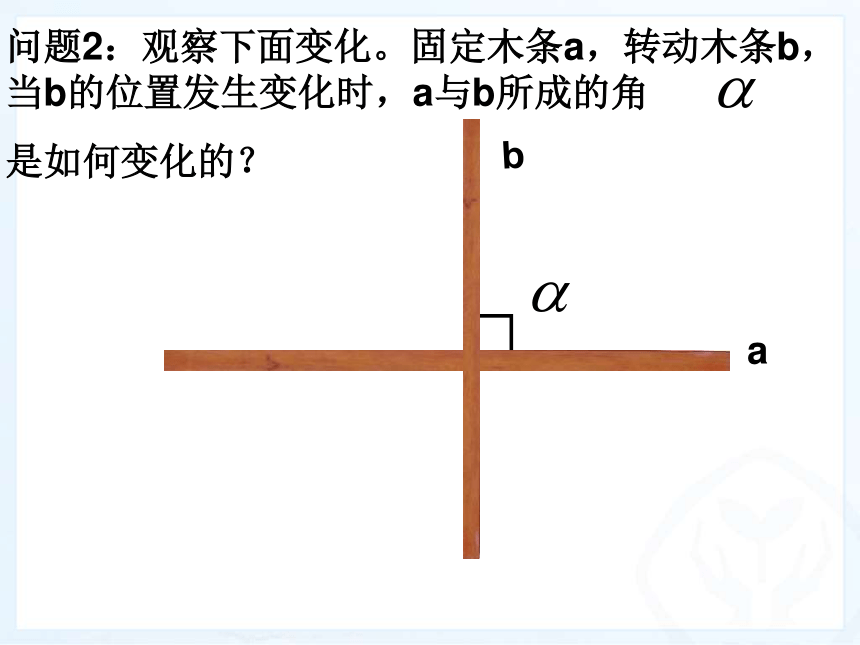
是如何变化的?ab一、复习引入:问题1:回忆邻补角、对顶角的定义及性质。(3分钟)ab问题2:观察下面变化。固定木条a,转动木条b,当b的位置发生变化时,a与b所成的角
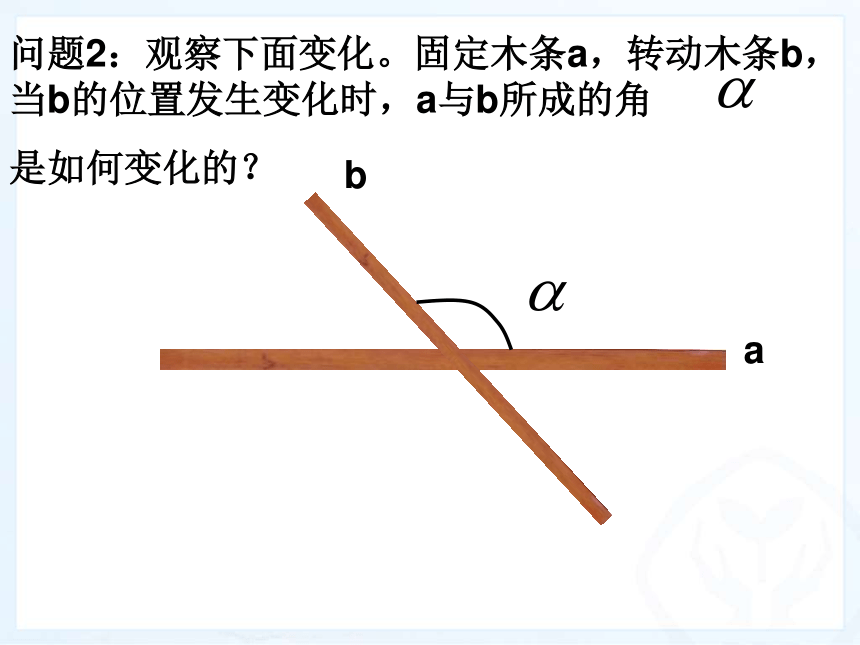
是如何变化的?ab问题2:观察下面变化。固定木条a,转动木条b,当b的位置发生变化时,a与b所成的角
是如何变化的?我国跳水运动员---田亮跳水运动员的入水姿势
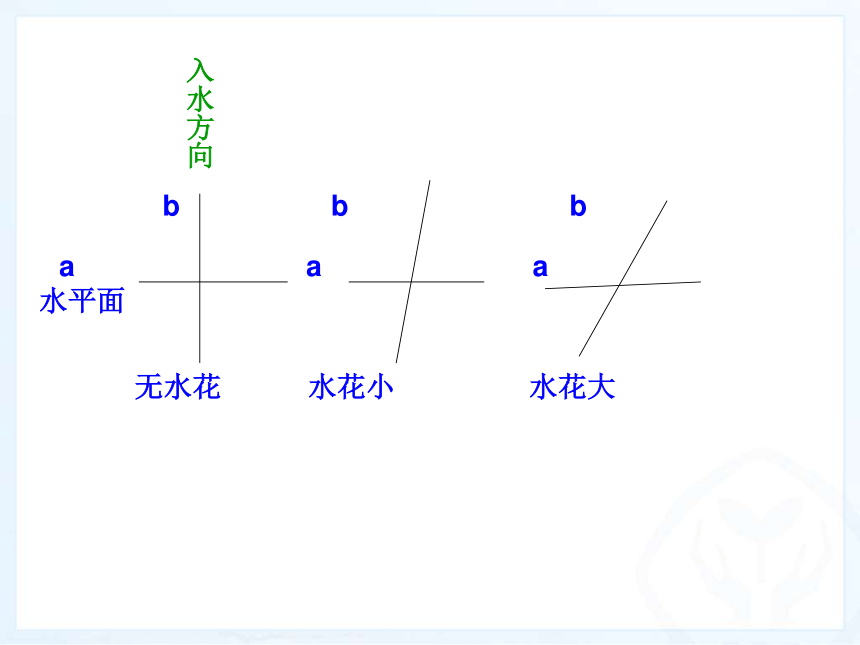
b b b
a a a
水平面
无水花 水花小 水花大
入水方向二、问题引领:(10分钟)
阅读课本第3页至第6页练习,思考以下问题:
1、两条直线相交所形成的夹角是在不断变化的。当它们的夹角是___°时,我们说这两条直线互相垂直。其中一条直线叫做另一条直线的______,它们的交点叫做____。
2、在垂线定义中包含了哪两种关系?如何用“因为”、“所以”表达这两种关系?
3、结合第4页探究中的三个问题可知条件不同,所得的_____也不同,三个问题中的条件分别是什么?结论分别是什么?
4、垂线的性质是什么?在性质中包含了哪两个特点?
5、结合第5页探究,动手画一画,哪一条线最特殊?你可以得到什么结论?
6、什么是点到直线的距离?它是一个___(填“数量或位置”)概念。
7、比例尺=___________,借助于比例尺我们可以进行_____与_______的转化。1、定义:
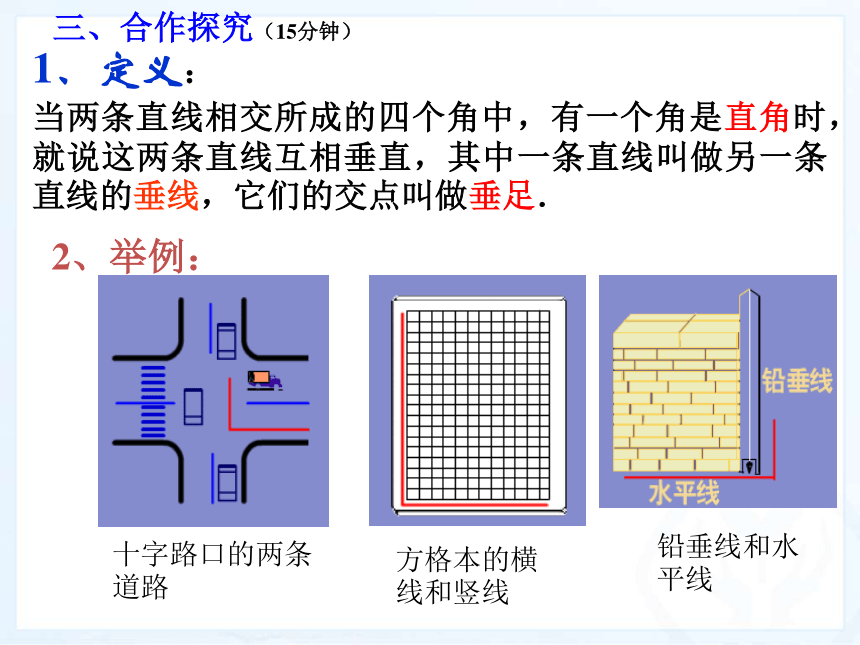
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
2、举例:三、合作探究(15分钟)两条直线垂直所形成的四个角之间的关系?相等3、知识生发:4、辨别:区分互相垂直与垂线区别:
互相垂直:两条直线的位置关系;
垂线:其中一条线对另一条线的命名。
联系:
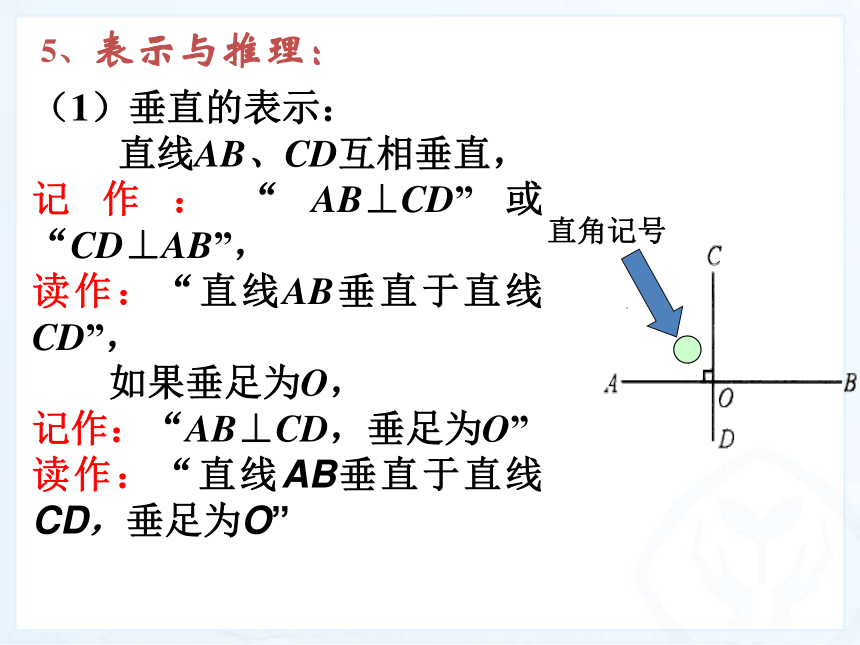
如果说两条直线“互相垂直”时,那么其中一条必定是另一条的“垂线”;如果一条直线是另一条直线的“垂线”,那么它们必定“互相垂直”。 5、表示与推理:(1)垂直的表示:
直线AB、CD互相垂直,
记作:“AB⊥CD”或“CD⊥AB”,
读作:“直线AB垂直于直线CD”,
如果垂足为O,
记作:“AB⊥CD,垂足为O”
读作:“直线AB垂直于直线 CD,垂足为O”
(2)垂直的定义的应用格式 ∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.这个推理过程可以写成: ∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:由数量关系得出位置关系由位置关系得出数量关系记作: MN⊥EF , 垂足为O.
或者MN⊥EF于点F记作: AB⊥OE,垂足为O.
或者AB⊥OE于点O练一练:
1)、写一写2)、选一选:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
(C)2、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1A问题2:
(1)两条直线垂直和相交是什么关系?(2)能否认为在同一平面内,两条直线的位置关系
有3种:相交,平行,垂直?垂直是相交的特殊情况不能,因为垂直是相交的特殊情况 答:
理由是:
∵ ∠1=35°,∠2=55°(已知)垂直∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴ OE⊥AB (垂直的定义)3)、算一算:(作业1)
(1)如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35° ∠2=55°,则OE与AB的位置关系是 ? (2):如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= (A)36° (B) 64°
(C)144° (D) 54° 54°练习:过点P画出射线AB或线段AB的垂线.(作业2)4)、画一画:
如何判定两条射线垂直?两条线段呢? 两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.复习:用三角板过一点作垂线的方法:
一靠:即三角板的一条直角边靠在已知直线也就是与已知直线重合;
二过:即三角板的另一条直角边过已知点;
三画,即画出垂线。问题1:已知直线l,能画出l的垂线吗?能画几条?
结果:与直线l垂直的垂线有无数多条,即存在,但有不确定性。问题2:在直线l上取一点A,过点A画l的垂线,如何画?能画几条?你从中得到什么结论?
结果:经过直线上一点有且只有一条直线与已知直线垂直。问题3:经过直线l外一点B画直线l的垂线,这样的垂线能画出几条?从中你又得出什么结论?
结果:经过直线外一点有且只有一条直线与已知直线垂直。六、探究:垂线的性质(5分钟)垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.垂线的存在性与唯一性
“有”表示存在,“只有”表示唯一,就是肯定有一条并且不能多于一条课堂练习(10分钟)1.选择题
C2.过点P分别向角的两边作垂线(作业3)3、如图,O为直线AB上的一点,∠AOC=-∠BOC,OC是∠AOD的平分线。(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由。(作业4)31ABOCD1、垂线段的概念:由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段.PlA要找垂线段, 先把点来看. 过点画垂线, 点足垂线段.例如:如图,PA⊥l于点A,线段PA叫做点P到直线l的垂线段.垂线段性质2的条探究 BDAOC1C2C3C4简单说成:垂线段最短.2、垂线段的性质: 连接直线外一点与直线上各点的所有线段中,垂线段最短.垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.ABPD特别强调:2.如图, AC⊥BC, ∠C=90°,线段AC、BC、CD中最短的是( )
(A)、AC (B)、BC (C)、CD (D)、不能确定1.已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条DABCDC例1、选择题:CADEB解:∵ AC⊥BC于C(已知)∴ AC<AB(垂线段最短)又∵ CD⊥AD于D(已知)∵ DE⊥BC于E(已知)∴ CD<AC(垂线段最短)∴ DE<CD(垂线段最短)∴ AB>AC>CD>DE例2、如图:AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段AB 、AC、DC和 DE的大小.直线外一点到这条直线的垂线段的
长度,叫做点到直线的距离.PA 例如:如图,PA⊥l于点A ,垂线段PA的长度叫做点P到直线l的距离. 例1:如图,是一个同学跳远的位置跳远成绩怎么表示? 解:过P点作PA⊥l于点A,垂线段PA的长度就是该同学的跳远成绩.3、点到直线的距离:DBCAE已知:如图AD<AE <AC<AB能说AD的长是A到BC的距离吗?答:不能.想一想:AB 例3、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离.ABCPQ∴BP=CQ例5、如图, (1)画出线段BC的中点M,连结AM; (2)比较点B与点C到直线AM的距离.例、1.如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长.MNMFABCDMN∴直线MF为所求垂线.4、区分:点与点之间的距离、点到线之间的距离1、如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.张庄∟解:点O即为所求。
理由是:垂线段最短五、拓展应用(7分钟)OABCDEFGM· ·问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线.并说明理由.问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么?问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线.┏
N拓展应用21、如图已知AC⊥BC,CD⊥AB,则图中
以________的长度表示点A到BC的距离;
以________的长度表示点B到AC的距离;
以________的长度表示点C到AB的距离.2、如图A,B,C三点在直线a上,M点在直线a外,AM⊥CM,MB⊥AC,在①MA>MB②MB>MC③MC>BC④AC>AM这四个结论中,正确的个数是( )个
A.1 B.2 C.3 D.4线段AC线段BC线段CDC 课堂测试(6分钟) 3、如图所示,在△ABC中,∠ABC=90 ,
①过点B作三角形ABC的AC边上的高BD,过D点作三角 形ABD的AB边上的高DE。
②点A到直线BC的距离是线段 .的长度.
点B到直线AC的距离是线段 .的长度.
点D到直线AB的距离是线段 . 的长度
线段AD的长度是点 .到直线 .的距离.ABBDDEABDED 3、垂线段的定义 4、点到直线的距离5、垂线的性质小结(2分钟)1、垂直的定义;
2、垂线的性质;作业:课本
第8页 第6、7题
第9页 第12题
是如何变化的?ab一、复习引入:问题1:回忆邻补角、对顶角的定义及性质。(3分钟)ab问题2:观察下面变化。固定木条a,转动木条b,当b的位置发生变化时,a与b所成的角
是如何变化的?ab问题2:观察下面变化。固定木条a,转动木条b,当b的位置发生变化时,a与b所成的角
是如何变化的?我国跳水运动员---田亮跳水运动员的入水姿势
b b b
a a a
水平面
无水花 水花小 水花大
入水方向二、问题引领:(10分钟)
阅读课本第3页至第6页练习,思考以下问题:
1、两条直线相交所形成的夹角是在不断变化的。当它们的夹角是___°时,我们说这两条直线互相垂直。其中一条直线叫做另一条直线的______,它们的交点叫做____。
2、在垂线定义中包含了哪两种关系?如何用“因为”、“所以”表达这两种关系?
3、结合第4页探究中的三个问题可知条件不同,所得的_____也不同,三个问题中的条件分别是什么?结论分别是什么?
4、垂线的性质是什么?在性质中包含了哪两个特点?
5、结合第5页探究,动手画一画,哪一条线最特殊?你可以得到什么结论?
6、什么是点到直线的距离?它是一个___(填“数量或位置”)概念。
7、比例尺=___________,借助于比例尺我们可以进行_____与_______的转化。1、定义:
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
2、举例:三、合作探究(15分钟)两条直线垂直所形成的四个角之间的关系?相等3、知识生发:4、辨别:区分互相垂直与垂线区别:
互相垂直:两条直线的位置关系;
垂线:其中一条线对另一条线的命名。
联系:
如果说两条直线“互相垂直”时,那么其中一条必定是另一条的“垂线”;如果一条直线是另一条直线的“垂线”,那么它们必定“互相垂直”。 5、表示与推理:(1)垂直的表示:
直线AB、CD互相垂直,
记作:“AB⊥CD”或“CD⊥AB”,
读作:“直线AB垂直于直线CD”,
如果垂足为O,
记作:“AB⊥CD,垂足为O”
读作:“直线AB垂直于直线 CD,垂足为O”
(2)垂直的定义的应用格式 ∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.这个推理过程可以写成: ∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:由数量关系得出位置关系由位置关系得出数量关系记作: MN⊥EF , 垂足为O.
或者MN⊥EF于点F记作: AB⊥OE,垂足为O.
或者AB⊥OE于点O练一练:
1)、写一写2)、选一选:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
(C)2、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1A问题2:
(1)两条直线垂直和相交是什么关系?(2)能否认为在同一平面内,两条直线的位置关系
有3种:相交,平行,垂直?垂直是相交的特殊情况不能,因为垂直是相交的特殊情况 答:
理由是:
∵ ∠1=35°,∠2=55°(已知)垂直∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴ OE⊥AB (垂直的定义)3)、算一算:(作业1)
(1)如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35° ∠2=55°,则OE与AB的位置关系是 ? (2):如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= (A)36° (B) 64°
(C)144° (D) 54° 54°练习:过点P画出射线AB或线段AB的垂线.(作业2)4)、画一画:
如何判定两条射线垂直?两条线段呢? 两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.复习:用三角板过一点作垂线的方法:
一靠:即三角板的一条直角边靠在已知直线也就是与已知直线重合;
二过:即三角板的另一条直角边过已知点;
三画,即画出垂线。问题1:已知直线l,能画出l的垂线吗?能画几条?
结果:与直线l垂直的垂线有无数多条,即存在,但有不确定性。问题2:在直线l上取一点A,过点A画l的垂线,如何画?能画几条?你从中得到什么结论?
结果:经过直线上一点有且只有一条直线与已知直线垂直。问题3:经过直线l外一点B画直线l的垂线,这样的垂线能画出几条?从中你又得出什么结论?
结果:经过直线外一点有且只有一条直线与已知直线垂直。六、探究:垂线的性质(5分钟)垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.垂线的存在性与唯一性
“有”表示存在,“只有”表示唯一,就是肯定有一条并且不能多于一条课堂练习(10分钟)1.选择题
C2.过点P分别向角的两边作垂线(作业3)3、如图,O为直线AB上的一点,∠AOC=-∠BOC,OC是∠AOD的平分线。(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由。(作业4)31ABOCD1、垂线段的概念:由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段.PlA要找垂线段, 先把点来看. 过点画垂线, 点足垂线段.例如:如图,PA⊥l于点A,线段PA叫做点P到直线l的垂线段.垂线段性质2的条探究 BDAOC1C2C3C4简单说成:垂线段最短.2、垂线段的性质: 连接直线外一点与直线上各点的所有线段中,垂线段最短.垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.ABPD特别强调:2.如图, AC⊥BC, ∠C=90°,线段AC、BC、CD中最短的是( )
(A)、AC (B)、BC (C)、CD (D)、不能确定1.已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条DABCDC例1、选择题:CADEB解:∵ AC⊥BC于C(已知)∴ AC<AB(垂线段最短)又∵ CD⊥AD于D(已知)∵ DE⊥BC于E(已知)∴ CD<AC(垂线段最短)∴ DE<CD(垂线段最短)∴ AB>AC>CD>DE例2、如图:AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段AB 、AC、DC和 DE的大小.直线外一点到这条直线的垂线段的
长度,叫做点到直线的距离.PA 例如:如图,PA⊥l于点A ,垂线段PA的长度叫做点P到直线l的距离. 例1:如图,是一个同学跳远的位置跳远成绩怎么表示? 解:过P点作PA⊥l于点A,垂线段PA的长度就是该同学的跳远成绩.3、点到直线的距离:DBCAE已知:如图AD<AE <AC<AB能说AD的长是A到BC的距离吗?答:不能.想一想:AB 例3、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离.ABCPQ∴BP=CQ例5、如图, (1)画出线段BC的中点M,连结AM; (2)比较点B与点C到直线AM的距离.例、1.如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长.MNMFABCDMN∴直线MF为所求垂线.4、区分:点与点之间的距离、点到线之间的距离1、如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.张庄∟解:点O即为所求。
理由是:垂线段最短五、拓展应用(7分钟)OABCDEFGM· ·问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线.并说明理由.问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么?问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线.┏
N拓展应用21、如图已知AC⊥BC,CD⊥AB,则图中
以________的长度表示点A到BC的距离;
以________的长度表示点B到AC的距离;
以________的长度表示点C到AB的距离.2、如图A,B,C三点在直线a上,M点在直线a外,AM⊥CM,MB⊥AC,在①MA>MB②MB>MC③MC>BC④AC>AM这四个结论中,正确的个数是( )个
A.1 B.2 C.3 D.4线段AC线段BC线段CDC 课堂测试(6分钟) 3、如图所示,在△ABC中,∠ABC=90 ,
①过点B作三角形ABC的AC边上的高BD,过D点作三角 形ABD的AB边上的高DE。
②点A到直线BC的距离是线段 .的长度.
点B到直线AC的距离是线段 .的长度.
点D到直线AB的距离是线段 . 的长度
线段AD的长度是点 .到直线 .的距离.ABBDDEABDED 3、垂线段的定义 4、点到直线的距离5、垂线的性质小结(2分钟)1、垂直的定义;
2、垂线的性质;作业:课本
第8页 第6、7题
第9页 第12题
