5.3.1平行线的性质
图片预览





文档简介
课件23张PPT。5.3.1 平行线的性质
(第1课时) 本课学习由平行线的判定引入对平行线性质的研究,先通过操作确认得到性质1,再经过简单推理得到性质2和性质3.学情分析学习目标:
(1)理解平行线的性质;
(2)经历平行线性质的探究过程,从中体会研究几何图形的一般方法。
学习重点:
平行线的性质的灵活应用。
学习难点:
得到平行线的性质的过程。 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.一、复习引入结论 1、平行线的判定(3分钟)两条平行线
被第三条直
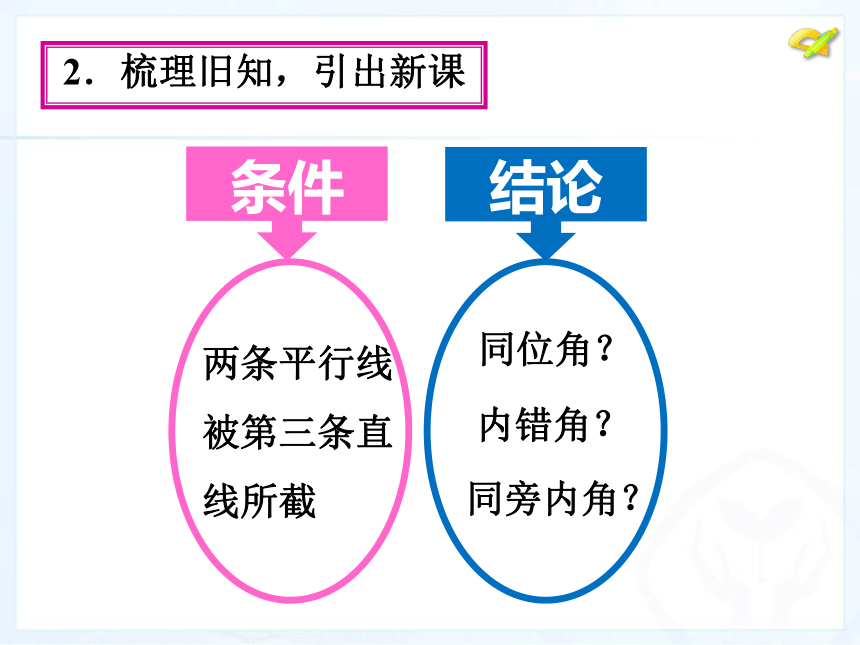
线所截2.梳理旧知,引出新课条件结论同位角?内错角?同旁内角?二、问题引领(10分钟)
阅读课本第18页至20页练习,思考以下问题:
1、结合第18页探究进行归纳,可得到什么结论?
2、如何由性质1得到性质2、3?
3、在性质1、2、3中的条件和结论分别是什么?
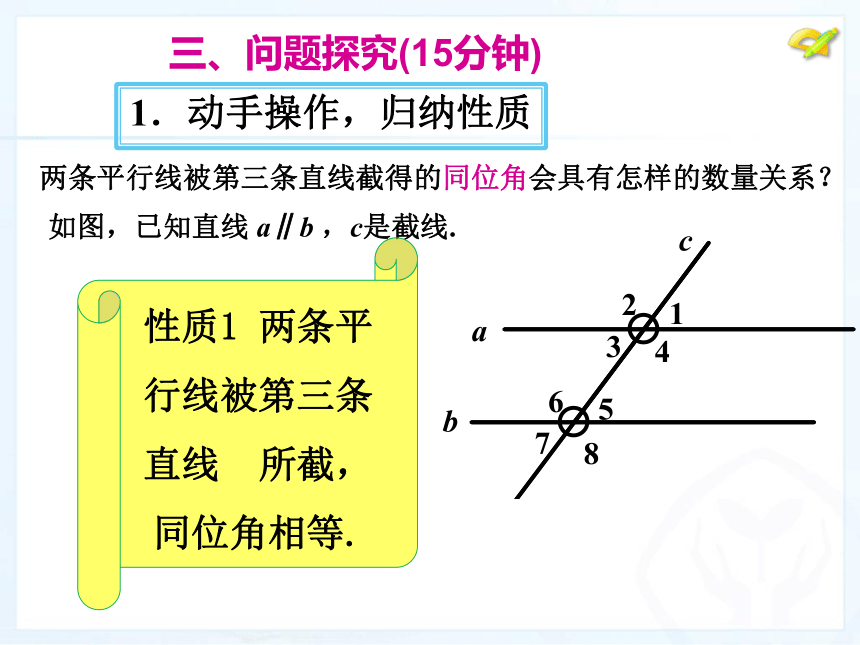
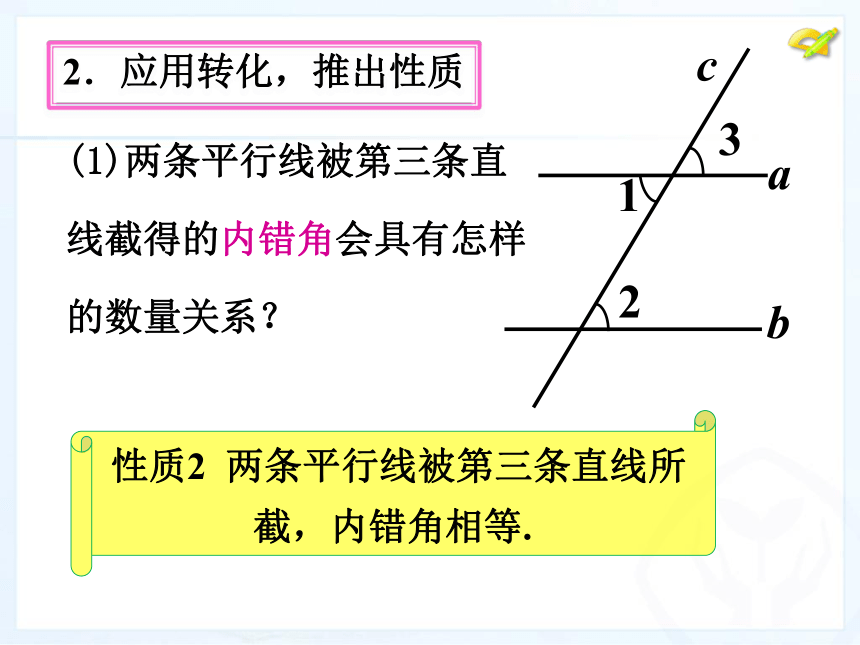
4、区分平行线性质和判定的不同。 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 1.动手操作,归纳性质 如图,已知直线 a∥b ,c是截线. 三、问题探究(15分钟)性质1 两条平行线被第三条直线 所截,同位角相等. 2.应用转化,推出性质性质2 两条平行线被第三条直线所截,内错角相等.(1)两条平行线被第三条直
线截得的内错角会具有怎样
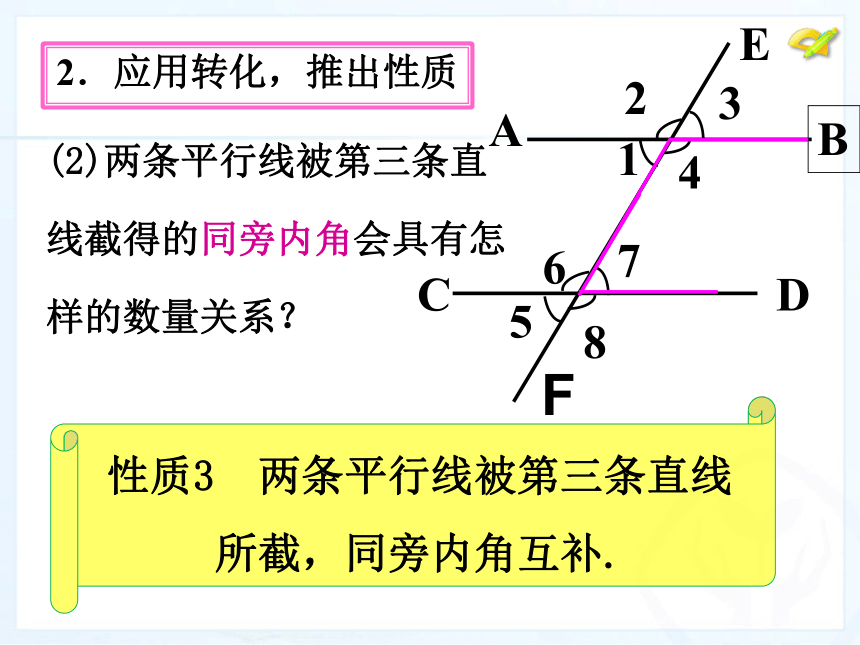
的数量关系? bac123 2.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.(2)两条平行线被第三条直
线截得的同旁内角会具有怎
样的数量关系? CDABE85612347F性质1 两条平行线被第三条直线所截,同位角相等.性质2 两条平行线被第三条直线所截,内错角相等.性质3 两条平行线被第三条直线所截,同旁内角互补.3、归纳总结(1)从∠1=110o可以知道
∠3是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠3 =110o.因为AB∥CD ,
∠1和∠3是同位角,根据两直
线平行,同位角相等,得到
∠1=∠3.因为∠1=110o,所以∠3 =110o.(2)从∠1=110o.可以知道∠2是多少度吗?为什么?4.巩固新知,深化理解答:∠2 =110o.因为AB∥CD,
∠1和∠2是内错角,根据
两直线平行,内错角相等,
得到∠1=∠2.因为∠1=110o,
所以∠2 =110o.例1 如图,平行线AB,CD被直线AE所截.(3)从∠1=110o可以知道∠4是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠4=70o.因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1+∠4=180o.因为∠1=110o,所以∠4=70o.例2 、如图是一块梯形铁片的残余部
分,量得∠A=100°, ∠B=115 ° ,
梯形另外两个角分别是多少度?DCAB5、实际应用(10分钟)四、基础练习(5分钟)1、如图,直线 a∥b ,∠1=54°,那么
∠ 2、 ∠ 3、 ∠ 4各是多少度?bac12342、如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°, ∠B=60°, ∠AED=60°.(1)DE和BC平行吗?为什么?
(2)∠C是多少度? 1、 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么? 五、拓展提高方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.1 五、拓展提高方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.2 五、拓展提高2、如图,
若 AD∥BC ,则
∠ = ∠ , ∠ = ∠ ,∠ABC+ ∠ =180°;
若DC∥AB,则∠ = ∠ ,
∠ = ∠ ,∠ABC+ ∠ =180°;3、如图, AB∥EF, CD∥EF ,∠B=40°、∠D=35 °,求∠BED的大小。(1)平行线的性质是什么?六.归纳小结(2)你能用自己的语言叙述研究平行线性质的过程吗? (3)性质2和性质3是通过简单推理得到的,在推理论证中需要注意哪些问题?(2分钟)教科书 习题5.3 第2、4、6题七.布置作业
(1)理解平行线的性质;
(2)经历平行线性质的探究过程,从中体会研究几何图形的一般方法。
学习重点:
平行线的性质的灵活应用。
学习难点:
得到平行线的性质的过程。 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.一、复习引入结论 1、平行线的判定(3分钟)两条平行线
被第三条直
线所截2.梳理旧知,引出新课条件结论同位角?内错角?同旁内角?二、问题引领(10分钟)
阅读课本第18页至20页练习,思考以下问题:
1、结合第18页探究进行归纳,可得到什么结论?
2、如何由性质1得到性质2、3?
3、在性质1、2、3中的条件和结论分别是什么?
4、区分平行线性质和判定的不同。 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 1.动手操作,归纳性质 如图,已知直线 a∥b ,c是截线. 三、问题探究(15分钟)性质1 两条平行线被第三条直线 所截,同位角相等. 2.应用转化,推出性质性质2 两条平行线被第三条直线所截,内错角相等.(1)两条平行线被第三条直
线截得的内错角会具有怎样
的数量关系? bac123 2.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.(2)两条平行线被第三条直
线截得的同旁内角会具有怎
样的数量关系? CDABE85612347F性质1 两条平行线被第三条直线所截,同位角相等.性质2 两条平行线被第三条直线所截,内错角相等.性质3 两条平行线被第三条直线所截,同旁内角互补.3、归纳总结(1)从∠1=110o可以知道
∠3是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠3 =110o.因为AB∥CD ,
∠1和∠3是同位角,根据两直
线平行,同位角相等,得到
∠1=∠3.因为∠1=110o,所以∠3 =110o.(2)从∠1=110o.可以知道∠2是多少度吗?为什么?4.巩固新知,深化理解答:∠2 =110o.因为AB∥CD,
∠1和∠2是内错角,根据
两直线平行,内错角相等,
得到∠1=∠2.因为∠1=110o,
所以∠2 =110o.例1 如图,平行线AB,CD被直线AE所截.(3)从∠1=110o可以知道∠4是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠4=70o.因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1+∠4=180o.因为∠1=110o,所以∠4=70o.例2 、如图是一块梯形铁片的残余部
分,量得∠A=100°, ∠B=115 ° ,
梯形另外两个角分别是多少度?DCAB5、实际应用(10分钟)四、基础练习(5分钟)1、如图,直线 a∥b ,∠1=54°,那么
∠ 2、 ∠ 3、 ∠ 4各是多少度?bac12342、如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°, ∠B=60°, ∠AED=60°.(1)DE和BC平行吗?为什么?
(2)∠C是多少度? 1、 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么? 五、拓展提高方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.1 五、拓展提高方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.2 五、拓展提高2、如图,
若 AD∥BC ,则
∠ = ∠ , ∠ = ∠ ,∠ABC+ ∠ =180°;
若DC∥AB,则∠ = ∠ ,
∠ = ∠ ,∠ABC+ ∠ =180°;3、如图, AB∥EF, CD∥EF ,∠B=40°、∠D=35 °,求∠BED的大小。(1)平行线的性质是什么?六.归纳小结(2)你能用自己的语言叙述研究平行线性质的过程吗? (3)性质2和性质3是通过简单推理得到的,在推理论证中需要注意哪些问题?(2分钟)教科书 习题5.3 第2、4、6题七.布置作业
