第十九章变量与函数导学案
图片预览




文档简介
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 变量与函数(一)
课型 总课时 2课时 第 1 课时 授课人
教学内容 教材71--71页
教学目标 1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;2、学会用含一个变量的代数式表示另一个变量;3、结合实例,理解函数的概念以及自变量的意义;在理解掌握函数概念的基础上,确定函数关系式;4、会根据函数解析式和实际意义确定自变量的取值范围。
教学重点 了解常量与变量的意义;理解函数概念和自变量的意义;确定函数关系式。
教学难点 函数概念的理解;函数关系式的确定
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 一、学前准备一辆汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.填表19--1,s的值随t的值的变化而变化吗? 1.请同学们根据题意填写下表:t/h12345S/km2.在以上这个过程中,变化的量是____________.不变化的量是__________.3.试用含t的式子表示s s=_____t的取值范围是 这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
引领自学 二、探究活动:活动一:思考并完成课本71-72页的问题1—4。 小结:在一个变化过程中,我们称数值发生变化的量为________;在一个变化过程中,我们称数值始终不变的量为________;
探究展示 活动二:问题引申,探索概念 (一)观察探究:1、在前面研究的每个问题中,都出现了______个变量,它们之间是相互影响,相互制约的.2、同一个问题中的变量之间有什么联系?(请同学们自己分析“问题一”中两个变量之间的关系,进而再分析上述所有实例中的两个变量之间是否有类似的关系.)3、其实,在一些用图或表格表达的问题中,也能看到两个变量间有上述这样的关系.我们来看课本96页思考的两个问题,通过观察、思考、讨论后回答: 归纳:上面每个问题中的两个变量相互联系,当其中一个变量取定一个值时,另一个变量就有________确定的值与其对应。(二)归纳概念: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是_________,y是x_____.如果当x=a时y=b,那么b叫做当自变量的值为a时的_________.
训练达标 1、若球体体积为V,半径为R,则V=R3.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,R的取值范围是 2、校园里栽下一棵小树高1.8米,以后每年长0.3米,则n年后的树高L与年数n之间的函数关系式__________.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,n的取值范围是 3、在男子1500米赛跑中,运动员的平均速度v= ,则这个关系式中变量是_______、_______,常量是________.自变量是 , 是 的函数,自变量的取值范围是 4、已知2x-3y=1,若把y看成x的函数,则可以表示为___________.其中变量是_____、_____,常量是________.自变量是 , 是 的函数,x的取值范围是 学生先在练习本上独立完成,然后指名学生回答。
总结反思 本节课你学会了什么 还有哪些疑惑? 学生总结发言。
作业布置 习题19.1 第1、2题
课后反思
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 变量与函数导学案(二)
课型 总课时 2课时 第 2 课时 授课人
教学内容 教材73--74页
教学目标 1.经过练习,观察,认识变量中的自变量与函数。. 2.会写出函数关系式,会求函数值.3.会确定自变量取值范围.
教学重点 会确定自变量的取值范围.
教学难点 函数概念的抽象性和列函数关系式
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 首先回顾上节活动中的问题.思考每个问题中是否有两个变量,变量间存在什么联系
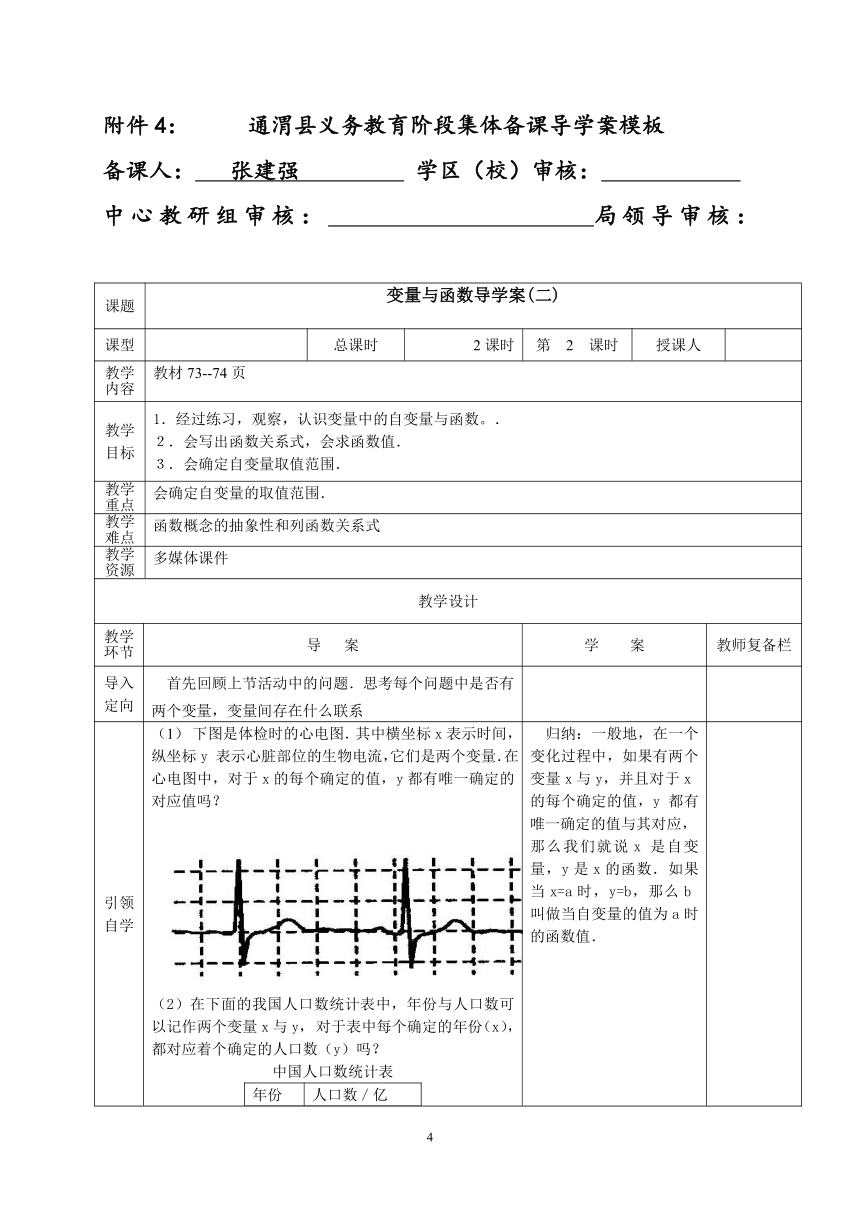
引领自学 (1) 下图是体检时的心电图.其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每个确定的值,y都有唯一确定的对应值吗? (2)在下面的我国人口数统计表中,年份与人口数可以记作两个变量x与y,对于表中每个确定的年份(x),都对应着个确定的人口数(y)吗?中国人口数统计表年份人口数/亿198410.34198911.06199411.76199912.52 归纳:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
引导点拨 例1 一辆汽车油箱现有汽油50L,如果不再加油,那么油箱中的油量y(L)随行驶里程x(km)的增加而减少,平均耗油量为0.1L/km. 1.写出表示y与x的函数关系式. 2.指出自变量x的取值范围. 3.汽车行驶200km时,油桶中还有多少汽油? 引导学生交流讨论,合作完成例1的解答过程。 问题:在上面所出现的各个函数关系式中,自变量的取值有限制吗 如果有.各是什么样的限制 用数学式子表示的函数的自变量取值范围
训练达标 1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子. (1).改变正方形的边长x,正方形的面积S随之改变. (2).秀水村的耕地面积是106m2,这个村人均占有耕地面积y随这个村人数n的变化而变化.2.校园里栽下一棵小树高1.8米,以后每年长0.3米,则n年后的树高L与年数n之间的函数关系式__________.3.在男子1500米赛跑中,运动员的平均速度v=,则这个关系式中________是自变量,________函数. 4.已知2x-3y=1,若把y看成x的函数,则可以表示为____________. 5.△ABC中,AB=AC,设∠B=x°,∠A=y°,试写出y与x的函数关系式_____________. 自我检测:1. 函数中,自变量x的取值范围是_________2. 面积是S(cm2)的正方形地板砖边长为a(cm),则S与a的关系式是______,其中自变量是______,____是_____的函数3. 函数的自变量x的取值范围是 . 4. 函数,当时,的取值范围是
总结反思 本节课你学会了什么 还有哪些疑惑?
作业布置 教材71页课后练习第1、2题
课后反思
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 函数的图像(一)
课型 总课时 2课时 第 1 课时 授课人
教学内容 教材75--77页
教学目标 1、使学生了解函数图象的意义;2、初步掌握画函数图象的方法(列表、描点、连线);3、学会通过观察、分析函数图象来获取相关信息;
教学重点 初步掌握画函数图象的方法;
教学难点 通过观察、分析函数图象来获取信息.
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 一、学前准备1.在一个变化过程中,我们称数值____________的量为变量;在一个变化过程中,我们称数值____________的量为常量. 2.长方形相邻两边长分别为x、y,面积为10,则用含x的式子表示y为____________,则这个问题中,____________是常量;________________是变量.3.一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是_________,y是x的________.如果当x=a时y=b,那么b叫做当自变量的值为a时的___________.已知三角形底边长为8,高为h,三角形的面积为s,则s与h的函数关系式为_______________,其中自变量是___________,自变量的函数是___________。 复习上节课的内容,检查对前面知识的掌握情况。
引领自学 二、探究活动:(一)函数图象的画法1、明确函数图象的意义: 2、描点法画函数图象:(二)解读函数图象信息思考:如图19.1-4是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化.你从图象中能得到哪些信息?可以认为,__________是________ 的函数,上图就是这个函数的图象。学生讨论完成76页思考中的问题1--3。 归纳总结:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的_________.强调:用 表示不在曲线上的点;在函数图象上的点要画成 的点.
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时 间?
(3)食堂离图书馆多远?小明从食堂到图书馆用了多 少时间?
(4)小明读报用了多长时间?(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
总结反思 通过本节课的学习同学们有什么收获?
学生总结发言
作业布置 习题19.1 第4、5、6题
课后反思
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 函数的图像(二)
课型 总课时 2课时 第 1 课时 授课人
教学内容 教材
教学目标 1.知道函数的三种表示方法;2.能用适当的函数表示法刻画简单实际问题中变量之间的关系; 3.结合对函数关系的分析,尝试对变量的变化规律进行初步预测.
教学重点 能用适当的函数表示法刻画简单实际问题中变量之间的关系
教学难点 结合对函数关系的分析,尝试对变量的变化规律进行初步预测
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 一、学前准备回忆描点法画函数图像的一般步骤 学生回答
引领自学 活动一:画出下列函数图像例3 在下列式子中,对于x的每一个确定的值,y有唯一的对应值,即y是x的函数。画出这些函数的图像:(1)y=x+0.5 活动二 函数的三种表示方法 学生分组交流讨论完成例3的(1)和(2)的函数图像,然后课件展示做函数图像的过程及方法。自学课本P80例4以上的内容并回答下列问题:1.函数的三种方法是什么?2.从前面的学习来看,你认为三种表示函数的方法各有什么优点?(小组交流自学成果并展示
探究展示 . 活动三 用适当的函数表示法刻画简单实际问题中变量之间的关系例4.一水库的水位在最近5小时内持续上涨,表19-6记录了这5小时内6个时间点的水位高度,其中t表示时间,y 表示水位高度。t/h012345y/m33.33.63.94.24.5(1)由记录表推出这5小时中的水位高度y(单位:米)随时间t(单位:时)变化的函数解析式,并画出函数图象;(2)据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米. 课件展示解答过程,巡视纠正学生出现的错误。 引导学生分析问题,体会利用函数解决实际问题的必要性,进一步了解数形结合的数学思想。
训练达标 教材81页练习第1---3题 学生课后完成
总结反思 本节课你学会了什么 还有哪些疑惑? 学生总结发言
作业布置 习题19.1 第8、9、10题
课后反思
PAGE
1
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 变量与函数(一)
课型 总课时 2课时 第 1 课时 授课人
教学内容 教材71--71页
教学目标 1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;2、学会用含一个变量的代数式表示另一个变量;3、结合实例,理解函数的概念以及自变量的意义;在理解掌握函数概念的基础上,确定函数关系式;4、会根据函数解析式和实际意义确定自变量的取值范围。
教学重点 了解常量与变量的意义;理解函数概念和自变量的意义;确定函数关系式。
教学难点 函数概念的理解;函数关系式的确定
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 一、学前准备一辆汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.填表19--1,s的值随t的值的变化而变化吗? 1.请同学们根据题意填写下表:t/h12345S/km2.在以上这个过程中,变化的量是____________.不变化的量是__________.3.试用含t的式子表示s s=_____t的取值范围是 这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
引领自学 二、探究活动:活动一:思考并完成课本71-72页的问题1—4。 小结:在一个变化过程中,我们称数值发生变化的量为________;在一个变化过程中,我们称数值始终不变的量为________;
探究展示 活动二:问题引申,探索概念 (一)观察探究:1、在前面研究的每个问题中,都出现了______个变量,它们之间是相互影响,相互制约的.2、同一个问题中的变量之间有什么联系?(请同学们自己分析“问题一”中两个变量之间的关系,进而再分析上述所有实例中的两个变量之间是否有类似的关系.)3、其实,在一些用图或表格表达的问题中,也能看到两个变量间有上述这样的关系.我们来看课本96页思考的两个问题,通过观察、思考、讨论后回答: 归纳:上面每个问题中的两个变量相互联系,当其中一个变量取定一个值时,另一个变量就有________确定的值与其对应。(二)归纳概念: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是_________,y是x_____.如果当x=a时y=b,那么b叫做当自变量的值为a时的_________.
训练达标 1、若球体体积为V,半径为R,则V=R3.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,R的取值范围是 2、校园里栽下一棵小树高1.8米,以后每年长0.3米,则n年后的树高L与年数n之间的函数关系式__________.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,n的取值范围是 3、在男子1500米赛跑中,运动员的平均速度v= ,则这个关系式中变量是_______、_______,常量是________.自变量是 , 是 的函数,自变量的取值范围是 4、已知2x-3y=1,若把y看成x的函数,则可以表示为___________.其中变量是_____、_____,常量是________.自变量是 , 是 的函数,x的取值范围是 学生先在练习本上独立完成,然后指名学生回答。
总结反思 本节课你学会了什么 还有哪些疑惑? 学生总结发言。
作业布置 习题19.1 第1、2题
课后反思
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 变量与函数导学案(二)
课型 总课时 2课时 第 2 课时 授课人
教学内容 教材73--74页
教学目标 1.经过练习,观察,认识变量中的自变量与函数。. 2.会写出函数关系式,会求函数值.3.会确定自变量取值范围.
教学重点 会确定自变量的取值范围.
教学难点 函数概念的抽象性和列函数关系式
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 首先回顾上节活动中的问题.思考每个问题中是否有两个变量,变量间存在什么联系
引领自学 (1) 下图是体检时的心电图.其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每个确定的值,y都有唯一确定的对应值吗? (2)在下面的我国人口数统计表中,年份与人口数可以记作两个变量x与y,对于表中每个确定的年份(x),都对应着个确定的人口数(y)吗?中国人口数统计表年份人口数/亿198410.34198911.06199411.76199912.52 归纳:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
引导点拨 例1 一辆汽车油箱现有汽油50L,如果不再加油,那么油箱中的油量y(L)随行驶里程x(km)的增加而减少,平均耗油量为0.1L/km. 1.写出表示y与x的函数关系式. 2.指出自变量x的取值范围. 3.汽车行驶200km时,油桶中还有多少汽油? 引导学生交流讨论,合作完成例1的解答过程。 问题:在上面所出现的各个函数关系式中,自变量的取值有限制吗 如果有.各是什么样的限制 用数学式子表示的函数的自变量取值范围
训练达标 1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子. (1).改变正方形的边长x,正方形的面积S随之改变. (2).秀水村的耕地面积是106m2,这个村人均占有耕地面积y随这个村人数n的变化而变化.2.校园里栽下一棵小树高1.8米,以后每年长0.3米,则n年后的树高L与年数n之间的函数关系式__________.3.在男子1500米赛跑中,运动员的平均速度v=,则这个关系式中________是自变量,________函数. 4.已知2x-3y=1,若把y看成x的函数,则可以表示为____________. 5.△ABC中,AB=AC,设∠B=x°,∠A=y°,试写出y与x的函数关系式_____________. 自我检测:1. 函数中,自变量x的取值范围是_________2. 面积是S(cm2)的正方形地板砖边长为a(cm),则S与a的关系式是______,其中自变量是______,____是_____的函数3. 函数的自变量x的取值范围是 . 4. 函数,当时,的取值范围是
总结反思 本节课你学会了什么 还有哪些疑惑?
作业布置 教材71页课后练习第1、2题
课后反思
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 函数的图像(一)
课型 总课时 2课时 第 1 课时 授课人
教学内容 教材75--77页
教学目标 1、使学生了解函数图象的意义;2、初步掌握画函数图象的方法(列表、描点、连线);3、学会通过观察、分析函数图象来获取相关信息;
教学重点 初步掌握画函数图象的方法;
教学难点 通过观察、分析函数图象来获取信息.
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 一、学前准备1.在一个变化过程中,我们称数值____________的量为变量;在一个变化过程中,我们称数值____________的量为常量. 2.长方形相邻两边长分别为x、y,面积为10,则用含x的式子表示y为____________,则这个问题中,____________是常量;________________是变量.3.一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是_________,y是x的________.如果当x=a时y=b,那么b叫做当自变量的值为a时的___________.已知三角形底边长为8,高为h,三角形的面积为s,则s与h的函数关系式为_______________,其中自变量是___________,自变量的函数是___________。 复习上节课的内容,检查对前面知识的掌握情况。
引领自学 二、探究活动:(一)函数图象的画法1、明确函数图象的意义: 2、描点法画函数图象:(二)解读函数图象信息思考:如图19.1-4是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化.你从图象中能得到哪些信息?可以认为,__________是________ 的函数,上图就是这个函数的图象。学生讨论完成76页思考中的问题1--3。 归纳总结:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的_________.强调:用 表示不在曲线上的点;在函数图象上的点要画成 的点.
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时 间?
(3)食堂离图书馆多远?小明从食堂到图书馆用了多 少时间?
(4)小明读报用了多长时间?(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
总结反思 通过本节课的学习同学们有什么收获?
学生总结发言
作业布置 习题19.1 第4、5、6题
课后反思
附件4: 通渭县义务教育阶段集体备课导学案模板
备课人: 张建强 学区(校)审核:
中心教研组审核: 局领导审核:
课题 函数的图像(二)
课型 总课时 2课时 第 1 课时 授课人
教学内容 教材
教学目标 1.知道函数的三种表示方法;2.能用适当的函数表示法刻画简单实际问题中变量之间的关系; 3.结合对函数关系的分析,尝试对变量的变化规律进行初步预测.
教学重点 能用适当的函数表示法刻画简单实际问题中变量之间的关系
教学难点 结合对函数关系的分析,尝试对变量的变化规律进行初步预测
教学资源 多媒体课件
教学设计
教学环节 导 案 学 案 教师复备栏
导入定向 一、学前准备回忆描点法画函数图像的一般步骤 学生回答
引领自学 活动一:画出下列函数图像例3 在下列式子中,对于x的每一个确定的值,y有唯一的对应值,即y是x的函数。画出这些函数的图像:(1)y=x+0.5 活动二 函数的三种表示方法 学生分组交流讨论完成例3的(1)和(2)的函数图像,然后课件展示做函数图像的过程及方法。自学课本P80例4以上的内容并回答下列问题:1.函数的三种方法是什么?2.从前面的学习来看,你认为三种表示函数的方法各有什么优点?(小组交流自学成果并展示
探究展示 . 活动三 用适当的函数表示法刻画简单实际问题中变量之间的关系例4.一水库的水位在最近5小时内持续上涨,表19-6记录了这5小时内6个时间点的水位高度,其中t表示时间,y 表示水位高度。t/h012345y/m33.33.63.94.24.5(1)由记录表推出这5小时中的水位高度y(单位:米)随时间t(单位:时)变化的函数解析式,并画出函数图象;(2)据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米. 课件展示解答过程,巡视纠正学生出现的错误。 引导学生分析问题,体会利用函数解决实际问题的必要性,进一步了解数形结合的数学思想。
训练达标 教材81页练习第1---3题 学生课后完成
总结反思 本节课你学会了什么 还有哪些疑惑? 学生总结发言
作业布置 习题19.1 第8、9、10题
课后反思
PAGE
1
