第二十六章 反比例函数达标测评卷(一)(含答案)
文档属性
| 名称 | 第二十六章 反比例函数达标测评卷(一)(含答案) | 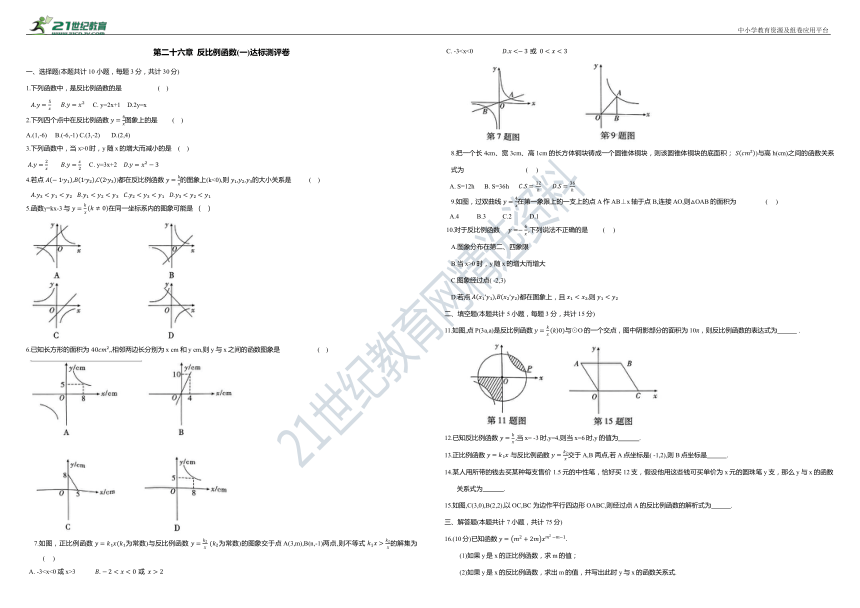 | |
| 格式 | docx | ||
| 文件大小 | 747.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 17:30:50 | ||
图片预览


文档简介
第二十六章 反比例函数(一)达标测评卷
一、选择题(本题共计10 小题,每题3 分,共计30分)
1.下列函数中,是反比例函数的是 ( )
C. y=2x+1 D.2y=x
2.下列四个点中在反比例函数图象上的是 ( )
A.(1,-6) B.(-6,-1) C.(3,-2) D.(2,4)
3.下列函数中,当x>0时,y随x的增大而减小的是 ( )
C. y=3x+2
4.若点 )都在反比例函数 的图象上(k<0),则 的大小关系是 ( )
5.函数γ=kx-3与 在同一坐标系内的图象可能是 ( )
6.已知长方形的面积为 ,相邻两边长分别为x cm 和y cm,则y与x之间的函数图象是 ( )
7.如图,正比例函数 为常数)与反比例函数 为常数)的图象交于点A(3,m),B(n,-1)两点,则不等式 的解集为 ( )
A. -33 或
C. -38.把一个长4cm、宽3cm、高1cm的长方体铜块铸成一个圆锥体铜块,则该圆锥体铜块的底面积; )与高h(cm)之间的函数关系式为 ( )
A. S=12h B. S=36h
9.如图,过双曲线 在第一象限上的一支上的点A作AB⊥x轴于点 B,连接AO,则△OAB的面积为 ( )
A.4 B.3 C.2 D.1
10.对于反比例函数 下列说法不正确的是 ( )
A.图象分布在第二、四象限
B.当x>0时,y随x的增大而增大
C.图象经过点( -2,3)
D.若点 都在图象上,且 则
二、填空题(本题共计5 小题,每题3 分,共计15 分)
11.如图,点 P(3a,a)是反比例函数 与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的表达式为 .
12.已知反比例函数 当x= -3时,y=4,则当x=6时,y的值为 .
13.正比例函数 与反比例函数 交于A,B 两点,若A点坐标是( -1,2),则B点坐标是 .
14.某人用所带的钱去买某种每支售价1.5元的中性笔,恰好买12支,假设他用这些钱可买单价为x元的圆珠笔y支,那么y与x的函数关系式为 .
15.如图,C(3,0),B(2,2),以OC,BC 为边作平行四边形OABC,则经过点A的反比例函数的解析式为 .
三、解答题(本题共计7 小题,共计 75 分)
16.(10分)已知函数
(1)如果y是x的正比例函数,求 m的值;
中小学教育资源及组卷应用平台
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
17.(8分)如图一次函数 的图象与反比例函数 的图象交于点A(-1,6),B(a;2):求一次函数和反比例函数的解析式.
18.(10分)如图,在直角坐标系中,四边形 OABC 是矩形,点D(1,4)是BC中点,反比例函数 的图象经过点D,并交 AB 于点 E.
(1)求k 的值;
(2)求五边形 OAEDC 的面积S.
19.(10分)某校准备在操场边建一个面积为600平方米的长方形劳动实践基地.
(1)求实践基地的长y(米)关于宽x(米)的函数表达式;
(2)由于受场地限制,实践基地的宽不能超过20米,则实践基地的长y至少为多少米
20.(12分)反比例函数 的图象经过点(
(1)求反比例函数的解析式;
(2)画出该函数的图象;
(3)当 时,求y的取值范围.
21.(12分)如图,一次函数 与反比例函数 的图象交于点A(2,6)和点B(m,1.5).
(1)试确定一次函数与反比例函数的表达式;
(2)连接 OA,OB,求 的面积;
(3)结合图象,直接写出不等式 的解集.
22.(13分)某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/时)与时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
(1)这场沙尘暴的最高风速是多少 最高风速维持了多长时间;
(2)求出当 时,风速y(千米/时)与时间x(小时)之间的函数关系式;
(3)在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间
1-10ABACB DADCD
11.
12. -2
13.(1,-2) 【解析】∵正比例函数y=h x和反比例函数 交于A,B两点,
∴A,B两点关于原点对称,
∵A 点的坐标为( -1,2),
∴B 点的坐标为(1,-2).
故答案为(1,-2).
16.解:(1)由 是正比例函数,得 且 解得 m =2 或m = -1;
(2)由 是反比例函数,得 且 解得m=1.
故y与x的函数关系式为
17.解:将A(-1,6)代入 得 m = -6,所以反比例函数解析式为
把B(a,2)代入
得 解得a= -3,
所以 B 点坐标为( -3,2),
把A(﹣1,6)和B(﹣3,2)代入γ=kx+b,得 解得
所以一次函数解析式为y=2x+8.
18.解:(1)把D(1,4)代入 得k=4,∴k=4;
(2)∵四边形 OABC 是矩形,
D(1,4)是 BC 中点,
∴BC=2CD=2,∴点 B 的坐标为(2,4),
把x=2 代入 得 ∴E(2,2),
∴S=2×4-1=7,
∴五边形 OAEDC 的面积为7.
19.解:(1)由长方形的面积为600 平方米,得xy=600,
即实践基地的长y(米)关于宽x(米)的函数表达式为
(2)∵600>0,∴在020.解:(1)把点(1,-2)代入 得m= -2,
(2)由(1)知,该反比例函数为 即该反比例函数图象上点的横、纵坐标的乘积为-2,其图象如图所示:
(3)由图象可知,当﹣221.解:(1)∵点A(2,6)在反比例函数 的图象上,
∴k=12,
∴反比例函数的表达式为
∵点B(m,1.5)在反比例函数 的图象上,
∴m=8,∴点 B的坐标为(8,1.5),
∵点A(2,6)和点B(8,1.5)都在一次函数γ=ax+b的图象上,
解得
∴一次函数的表达式为
(2)令直线 与y轴交于点 C,与x轴交于点D,
当x=0时, ∴点C 的坐标为(o, ),当y=0时, 解得x=10.
∴点D 的坐标为(10,0),
(3)由图象可知不等式 的解集是08.
22.解:(1)0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8﹢(10﹣4)×4=32(千米/时);
10~20时,风速不变,最高风速维持的时间为20–10=10(小时);
答:这场沙尘暴的最高风速是32 千米/时,最高风速维持了10小时;
(2)设 将(20,32)代入,得 解得 k=640,
所以当x≥20时,风速y(千米/时)与时间x(小时)之间的函数关系式为
(3)∵4 时风速为8千米/时,而4 小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,将γ=10代入 得 解得 x=64,
∴64﹣4.5=59.5(小时),
故沙尘暴的风速从开始形成过程中的 10千米/小时到最后减弱过程中的10 千米/小时,共经过59.5小时.
答:这次风暴的整个过程中,“危险时刻”一共经过59.5小时,
一、选择题(本题共计10 小题,每题3 分,共计30分)
1.下列函数中,是反比例函数的是 ( )
C. y=2x+1 D.2y=x
2.下列四个点中在反比例函数图象上的是 ( )
A.(1,-6) B.(-6,-1) C.(3,-2) D.(2,4)
3.下列函数中,当x>0时,y随x的增大而减小的是 ( )
C. y=3x+2
4.若点 )都在反比例函数 的图象上(k<0),则 的大小关系是 ( )
5.函数γ=kx-3与 在同一坐标系内的图象可能是 ( )
6.已知长方形的面积为 ,相邻两边长分别为x cm 和y cm,则y与x之间的函数图象是 ( )
7.如图,正比例函数 为常数)与反比例函数 为常数)的图象交于点A(3,m),B(n,-1)两点,则不等式 的解集为 ( )
A. -3
C. -3
A. S=12h B. S=36h
9.如图,过双曲线 在第一象限上的一支上的点A作AB⊥x轴于点 B,连接AO,则△OAB的面积为 ( )
A.4 B.3 C.2 D.1
10.对于反比例函数 下列说法不正确的是 ( )
A.图象分布在第二、四象限
B.当x>0时,y随x的增大而增大
C.图象经过点( -2,3)
D.若点 都在图象上,且 则
二、填空题(本题共计5 小题,每题3 分,共计15 分)
11.如图,点 P(3a,a)是反比例函数 与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的表达式为 .
12.已知反比例函数 当x= -3时,y=4,则当x=6时,y的值为 .
13.正比例函数 与反比例函数 交于A,B 两点,若A点坐标是( -1,2),则B点坐标是 .
14.某人用所带的钱去买某种每支售价1.5元的中性笔,恰好买12支,假设他用这些钱可买单价为x元的圆珠笔y支,那么y与x的函数关系式为 .
15.如图,C(3,0),B(2,2),以OC,BC 为边作平行四边形OABC,则经过点A的反比例函数的解析式为 .
三、解答题(本题共计7 小题,共计 75 分)
16.(10分)已知函数
(1)如果y是x的正比例函数,求 m的值;
中小学教育资源及组卷应用平台
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
17.(8分)如图一次函数 的图象与反比例函数 的图象交于点A(-1,6),B(a;2):求一次函数和反比例函数的解析式.
18.(10分)如图,在直角坐标系中,四边形 OABC 是矩形,点D(1,4)是BC中点,反比例函数 的图象经过点D,并交 AB 于点 E.
(1)求k 的值;
(2)求五边形 OAEDC 的面积S.
19.(10分)某校准备在操场边建一个面积为600平方米的长方形劳动实践基地.
(1)求实践基地的长y(米)关于宽x(米)的函数表达式;
(2)由于受场地限制,实践基地的宽不能超过20米,则实践基地的长y至少为多少米
20.(12分)反比例函数 的图象经过点(
(1)求反比例函数的解析式;
(2)画出该函数的图象;
(3)当 时,求y的取值范围.
21.(12分)如图,一次函数 与反比例函数 的图象交于点A(2,6)和点B(m,1.5).
(1)试确定一次函数与反比例函数的表达式;
(2)连接 OA,OB,求 的面积;
(3)结合图象,直接写出不等式 的解集.
22.(13分)某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/时)与时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
(1)这场沙尘暴的最高风速是多少 最高风速维持了多长时间;
(2)求出当 时,风速y(千米/时)与时间x(小时)之间的函数关系式;
(3)在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间
1-10ABACB DADCD
11.
12. -2
13.(1,-2) 【解析】∵正比例函数y=h x和反比例函数 交于A,B两点,
∴A,B两点关于原点对称,
∵A 点的坐标为( -1,2),
∴B 点的坐标为(1,-2).
故答案为(1,-2).
16.解:(1)由 是正比例函数,得 且 解得 m =2 或m = -1;
(2)由 是反比例函数,得 且 解得m=1.
故y与x的函数关系式为
17.解:将A(-1,6)代入 得 m = -6,所以反比例函数解析式为
把B(a,2)代入
得 解得a= -3,
所以 B 点坐标为( -3,2),
把A(﹣1,6)和B(﹣3,2)代入γ=kx+b,得 解得
所以一次函数解析式为y=2x+8.
18.解:(1)把D(1,4)代入 得k=4,∴k=4;
(2)∵四边形 OABC 是矩形,
D(1,4)是 BC 中点,
∴BC=2CD=2,∴点 B 的坐标为(2,4),
把x=2 代入 得 ∴E(2,2),
∴S=2×4-1=7,
∴五边形 OAEDC 的面积为7.
19.解:(1)由长方形的面积为600 平方米,得xy=600,
即实践基地的长y(米)关于宽x(米)的函数表达式为
(2)∵600>0,∴在0
(2)由(1)知,该反比例函数为 即该反比例函数图象上点的横、纵坐标的乘积为-2,其图象如图所示:
(3)由图象可知,当﹣2
∴k=12,
∴反比例函数的表达式为
∵点B(m,1.5)在反比例函数 的图象上,
∴m=8,∴点 B的坐标为(8,1.5),
∵点A(2,6)和点B(8,1.5)都在一次函数γ=ax+b的图象上,
解得
∴一次函数的表达式为
(2)令直线 与y轴交于点 C,与x轴交于点D,
当x=0时, ∴点C 的坐标为(o, ),当y=0时, 解得x=10.
∴点D 的坐标为(10,0),
(3)由图象可知不等式 的解集是0
22.解:(1)0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8﹢(10﹣4)×4=32(千米/时);
10~20时,风速不变,最高风速维持的时间为20–10=10(小时);
答:这场沙尘暴的最高风速是32 千米/时,最高风速维持了10小时;
(2)设 将(20,32)代入,得 解得 k=640,
所以当x≥20时,风速y(千米/时)与时间x(小时)之间的函数关系式为
(3)∵4 时风速为8千米/时,而4 小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,将γ=10代入 得 解得 x=64,
∴64﹣4.5=59.5(小时),
故沙尘暴的风速从开始形成过程中的 10千米/小时到最后减弱过程中的10 千米/小时,共经过59.5小时.
答:这次风暴的整个过程中,“危险时刻”一共经过59.5小时,
