第二十八章 锐角三角函数综合测评卷(二)(含答案)
文档属性
| 名称 | 第二十八章 锐角三角函数综合测评卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 910.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 17:35:35 | ||
图片预览

文档简介
第二十八章 锐角三角函数(二)综合测评卷
一、选择题(本题共计10小题,每题3分,共计30分)
1.在△ABC中, 则 sinB 的值为 ( )
D.3
2.在Rt△ABC中,∠C=90°,如果 那么 sinB 的值是 ( )
D.3
3.在△ABC中, 那么 tanA 等于 ( )
4.当 时,以下结论正确的是 ( )
D.以上都不对
5.如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是 ( )
A. sinA的值越小,梯子越陡 B. cosA 的值越小,梯子越陡
C. tanA 的值越小,梯子越陡D.陡缓程度与 的函数值无关
6.如图, 的顶点均在正方形网格的格点上,则, 的正弦值为 ( )
7.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为 ,缆车速度为每分钟40米,从山脚下A到达山顶 B 缆车需要 15 分钟,则山的高度 BC 为( )米.
8.如图,为测量某物体 AB 的高度,在D 点测得 A 点的仰角为 朝物体AB方向前进20米,到达点C,再次测得点A的仰角为 则物体 AB 的高度为 ( )
A.10 米 米 米 米
9.如图,一艘客轮从小岛A沿东北方向航行,同时一艘补给船从小岛A正东方向相距 海里的港口B 出发,沿北偏西60°方向航行,与客轮同时到达C处给客轮进行补给,则客轮与补给船的速度之比为 ( )
10.如图所示,CD是一个平面镜,光线从A 点射出经 CD上的E点反射后照射到B点,设入射角为α(反射角等于入射角), 垂足分别为 C,D.若 12,则 tanα的值为 ( )
二、填空题(本题共计5 小题,每题3 分,共计15分)
11.如图,在平面直角坐标系中,点A在x轴的正半轴上,点B坐标为(4,3),则tan∠AOB 的值为 .
12.如图,在 的正方形网格中, 的顶点都在小正方形的顶点上,则 tanA 的值是 .
13.如图,在Rt△ABC中,∠ACB=90°,点D为AB 边的中点,连接CD,若BC=4,CD=3,则 cos∠DCB 的值为 .
14.如图,一条铁路路基的横断面为等腰梯形,根据图示数据计算路基的下底宽
15.如图,某渔船在海面上朝正东方向匀速航行,在 A 处观测到灯塔 M 在北偏东 方向上,且AM=100海里.那么该船继续航行 海里可使渔船到达离灯塔距离最近的位置.
三、解答题(本题共计8 小题,共计75 分)
16.(8分)计算:
中小学教育资源及组卷应用平台
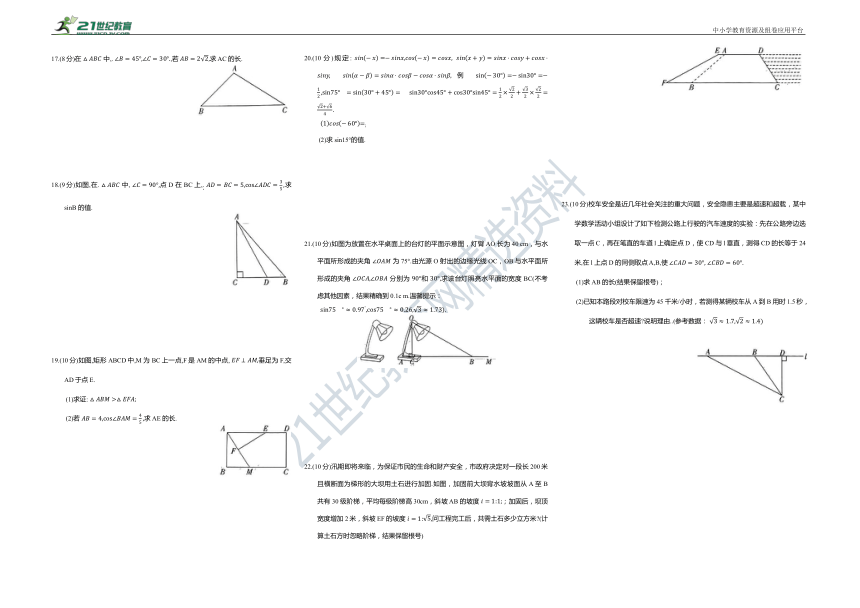
17.(8分)在 中,. ,若 求 AC的长.
18.(9分)如图,在. 中, 点 D 在 BC 上,. 求 sinB 的值.
19.(10分)如图,矩形ABCD中,M 为 BC上一点,F是AM的中点, 垂足为 F,交 AD于点E.
(1)求证:
(2)若 求AE 的长.
20.(10分)规定: 例
(2)求 sin15°的值.
21.(10分)如图为放置在水平桌面上的台灯的平面示意图,灯臂AO 长为40 cm,与水平面所形成的夹角 为75°.由光源O 射出的边缘光线OC,OB与水平面所形成的夹角 分别为 和 求该台灯照亮水平面的宽度 BC(不考虑其他因素,结果精确到0.1c m.温馨提示:
22.(10分)汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至 B共有30 级阶梯,平均每级阶梯高 30cm,斜坡 AB 的坡度 ;加固后,坝顶宽度增加2米,斜坡EF的坡度 问工程完工后,共需土石多少立方米 (计算土石方时忽略阶梯,结果保留根号)
23.(10分)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点 D,使 CD与l垂直,测得CD的长等于 24 米,在l 上点 D 的同侧取点 A,B,使
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45 千米/小时,若测得某辆校车从A到B用时1.5秒,这辆校车是否超速 说明理由..(参考数据:
1-10BADAB BCBAD
11. 【解析】过点 B作x轴的垂线,交x轴于点 C,
∵点B(4,3),BC⊥OA,
∴OC=4,BC=3,
故答案为 .
12. 【解析】过点B作BD⊥AC,
设小正方形的边长为1,则BC=BE=2,AE=4,由勾股定理,得
即 解得 由勾股定理得 故答案为 .
13. 【解析】∵ ∠ACB =90°,点 D 为 AB 边的中点,. .故答案为 .
14.34 【解析】作 DE⊥AB 于点E,CF⊥AB 于点F,那么EF=CD=10 米,
∵坡度为1:2,DE=6米,
∴AE=FG=12 米,
∴AG=12+10+12=34(米).故答案为 34.
【解析】
如图,过 M 作东西方向的垂线,设垂足为 N.易知:∠MAN=90°-60°=30°.
在 Rt△AMN中,∠ANM =90°,∠MAN =30°,AM = 100 海里,则 AN = AM · cos∠MAN = (海里).故该船继续航行50 海里可使渔船到达离灯塔距离最近的位置.
16.解:(1)原式 (2)原式
17.解:过点A作AD⊥BC 于点D,
在直角三角形ABD中,∠B=45°,
∴AD=AB·sinB =2,
在直角三角形ADC中,∠C=30°,∴AC=2AD=4.
18.解:
∴CD =3,
∴在Rt△ACD中,
∴在 Rt△ACB中,
19.解:(1)∵四边形 ABCD 是矩形,
∴ ∠B=∠BAD=90°,
∵ EF⊥AM,∴ ∠AFE=∠B=∠BAD=90°,
∴ ∠BAM +∠EAF=∠AEF+∠EAF=90°,即∠BAM =∠AEF,∴ △ABM∽△EFA;
(2)在Rt△ABM中,∠B=90°,AB=4,
∵F 为 AM 中点,∴AF=2.5,
∵∠BAM=∠AEF,
在 Rt△AEF 中,
20.解:(1)由题意知, 故答案为 ;
21.解:在直角三角形ACO 中,
解得 OC≈38.8,
在直角三角形 BCO 中, 解得BC≈67.3.
答:该台灯照亮水平面的宽度 BC 大约是67,3 cm.
22.解:过点A作AH⊥BC于点H,过点E作EG⊥BC 于点 G,
则四边形 EGHA是矩形,
∴EG=AH,GH=AE=2米,
∵AH=30×30=900(cm)=9(米),
又斜坡 AB 的坡度i=1:1,
∴AH=BH=9米,∴BG=BH-HG=7米,
∵ 斜坡 EF 的坡度i=1: ,∴FG=9 米,
∴BF=FG-BG=(9 -7)米,
∴共需土石为
立方米.
23.解:(1)由题意,得在Rt△ADC中,
解得
在 Rt△BDC中,
解得
(米);
(2)汽车从A 到 B 用时 1.5 秒,所以速度为 (米/秒),
18.1米/秒=65.16 千米/小时>45 千米/小时,..此校车在AB 路段超速.
一、选择题(本题共计10小题,每题3分,共计30分)
1.在△ABC中, 则 sinB 的值为 ( )
D.3
2.在Rt△ABC中,∠C=90°,如果 那么 sinB 的值是 ( )
D.3
3.在△ABC中, 那么 tanA 等于 ( )
4.当 时,以下结论正确的是 ( )
D.以上都不对
5.如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是 ( )
A. sinA的值越小,梯子越陡 B. cosA 的值越小,梯子越陡
C. tanA 的值越小,梯子越陡D.陡缓程度与 的函数值无关
6.如图, 的顶点均在正方形网格的格点上,则, 的正弦值为 ( )
7.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为 ,缆车速度为每分钟40米,从山脚下A到达山顶 B 缆车需要 15 分钟,则山的高度 BC 为( )米.
8.如图,为测量某物体 AB 的高度,在D 点测得 A 点的仰角为 朝物体AB方向前进20米,到达点C,再次测得点A的仰角为 则物体 AB 的高度为 ( )
A.10 米 米 米 米
9.如图,一艘客轮从小岛A沿东北方向航行,同时一艘补给船从小岛A正东方向相距 海里的港口B 出发,沿北偏西60°方向航行,与客轮同时到达C处给客轮进行补给,则客轮与补给船的速度之比为 ( )
10.如图所示,CD是一个平面镜,光线从A 点射出经 CD上的E点反射后照射到B点,设入射角为α(反射角等于入射角), 垂足分别为 C,D.若 12,则 tanα的值为 ( )
二、填空题(本题共计5 小题,每题3 分,共计15分)
11.如图,在平面直角坐标系中,点A在x轴的正半轴上,点B坐标为(4,3),则tan∠AOB 的值为 .
12.如图,在 的正方形网格中, 的顶点都在小正方形的顶点上,则 tanA 的值是 .
13.如图,在Rt△ABC中,∠ACB=90°,点D为AB 边的中点,连接CD,若BC=4,CD=3,则 cos∠DCB 的值为 .
14.如图,一条铁路路基的横断面为等腰梯形,根据图示数据计算路基的下底宽
15.如图,某渔船在海面上朝正东方向匀速航行,在 A 处观测到灯塔 M 在北偏东 方向上,且AM=100海里.那么该船继续航行 海里可使渔船到达离灯塔距离最近的位置.
三、解答题(本题共计8 小题,共计75 分)
16.(8分)计算:
中小学教育资源及组卷应用平台
17.(8分)在 中,. ,若 求 AC的长.
18.(9分)如图,在. 中, 点 D 在 BC 上,. 求 sinB 的值.
19.(10分)如图,矩形ABCD中,M 为 BC上一点,F是AM的中点, 垂足为 F,交 AD于点E.
(1)求证:
(2)若 求AE 的长.
20.(10分)规定: 例
(2)求 sin15°的值.
21.(10分)如图为放置在水平桌面上的台灯的平面示意图,灯臂AO 长为40 cm,与水平面所形成的夹角 为75°.由光源O 射出的边缘光线OC,OB与水平面所形成的夹角 分别为 和 求该台灯照亮水平面的宽度 BC(不考虑其他因素,结果精确到0.1c m.温馨提示:
22.(10分)汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至 B共有30 级阶梯,平均每级阶梯高 30cm,斜坡 AB 的坡度 ;加固后,坝顶宽度增加2米,斜坡EF的坡度 问工程完工后,共需土石多少立方米 (计算土石方时忽略阶梯,结果保留根号)
23.(10分)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点 D,使 CD与l垂直,测得CD的长等于 24 米,在l 上点 D 的同侧取点 A,B,使
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45 千米/小时,若测得某辆校车从A到B用时1.5秒,这辆校车是否超速 说明理由..(参考数据:
1-10BADAB BCBAD
11. 【解析】过点 B作x轴的垂线,交x轴于点 C,
∵点B(4,3),BC⊥OA,
∴OC=4,BC=3,
故答案为 .
12. 【解析】过点B作BD⊥AC,
设小正方形的边长为1,则BC=BE=2,AE=4,由勾股定理,得
即 解得 由勾股定理得 故答案为 .
13. 【解析】∵ ∠ACB =90°,点 D 为 AB 边的中点,. .故答案为 .
14.34 【解析】作 DE⊥AB 于点E,CF⊥AB 于点F,那么EF=CD=10 米,
∵坡度为1:2,DE=6米,
∴AE=FG=12 米,
∴AG=12+10+12=34(米).故答案为 34.
【解析】
如图,过 M 作东西方向的垂线,设垂足为 N.易知:∠MAN=90°-60°=30°.
在 Rt△AMN中,∠ANM =90°,∠MAN =30°,AM = 100 海里,则 AN = AM · cos∠MAN = (海里).故该船继续航行50 海里可使渔船到达离灯塔距离最近的位置.
16.解:(1)原式 (2)原式
17.解:过点A作AD⊥BC 于点D,
在直角三角形ABD中,∠B=45°,
∴AD=AB·sinB =2,
在直角三角形ADC中,∠C=30°,∴AC=2AD=4.
18.解:
∴CD =3,
∴在Rt△ACD中,
∴在 Rt△ACB中,
19.解:(1)∵四边形 ABCD 是矩形,
∴ ∠B=∠BAD=90°,
∵ EF⊥AM,∴ ∠AFE=∠B=∠BAD=90°,
∴ ∠BAM +∠EAF=∠AEF+∠EAF=90°,即∠BAM =∠AEF,∴ △ABM∽△EFA;
(2)在Rt△ABM中,∠B=90°,AB=4,
∵F 为 AM 中点,∴AF=2.5,
∵∠BAM=∠AEF,
在 Rt△AEF 中,
20.解:(1)由题意知, 故答案为 ;
21.解:在直角三角形ACO 中,
解得 OC≈38.8,
在直角三角形 BCO 中, 解得BC≈67.3.
答:该台灯照亮水平面的宽度 BC 大约是67,3 cm.
22.解:过点A作AH⊥BC于点H,过点E作EG⊥BC 于点 G,
则四边形 EGHA是矩形,
∴EG=AH,GH=AE=2米,
∵AH=30×30=900(cm)=9(米),
又斜坡 AB 的坡度i=1:1,
∴AH=BH=9米,∴BG=BH-HG=7米,
∵ 斜坡 EF 的坡度i=1: ,∴FG=9 米,
∴BF=FG-BG=(9 -7)米,
∴共需土石为
立方米.
23.解:(1)由题意,得在Rt△ADC中,
解得
在 Rt△BDC中,
解得
(米);
(2)汽车从A 到 B 用时 1.5 秒,所以速度为 (米/秒),
18.1米/秒=65.16 千米/小时>45 千米/小时,..此校车在AB 路段超速.
