数学人教A版(2019)选择性必修第二册4.1.1数列的概念与通项公式 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.1.1数列的概念与通项公式 课件(共21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 20:18:47 | ||
图片预览








文档简介
(共21张PPT)
4.1.1 数列的概念与通项
1.能准确说出数列的概念及其表示方法(重点、难点)
2.会用通项公式写出数列的任意一项
3.对于比较简单的数列,会根据给定的前几项写出它的一个通项公式(易错点)
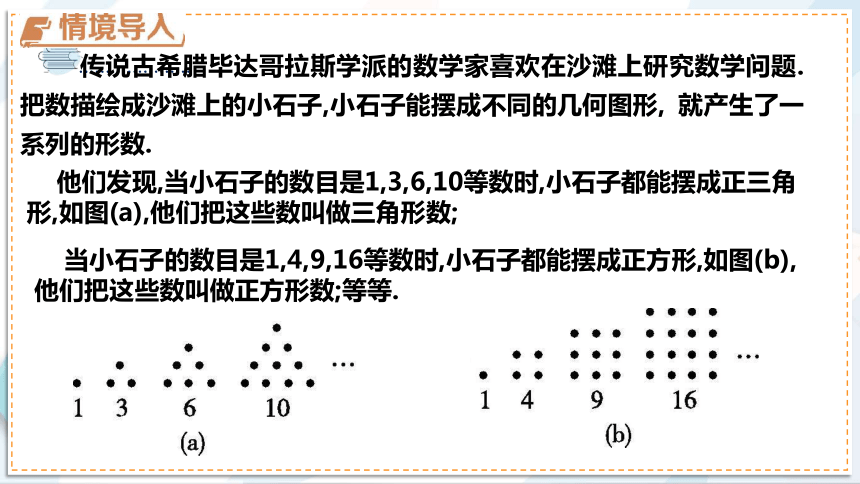
传说古希腊毕达哥拉斯学派的数学家喜欢在沙滩上研究数学问题. 把数描绘成沙滩上的小石子,小石子能摆成不同的几何图形, 就产生了一系列的形数.
他们发现,当小石子的数目是1,3,6,10等数时,小石子都能摆成正三角形,如图(a),他们把这些数叫做三角形数;
当小石子的数目是1,4,9,16等数时,小石子都能摆成正方形,如图(b),他们把这些数叫做正方形数;等等.
实例1:王芳从1岁到17岁每年的身高依次排成一列数:
问题1 :它们之间能否交换位置?具有确定的顺序吗?
第1年
第2年
第3年
.......
不能交换位置,并且具有确定的顺序.
记王芳第i岁时的身高为,则有:
新知探究
实例2:在两河流域发掘的一块泥版上就有一列依次表示一个月中
从第1天到第15天每天月亮可见部分的数∶5,10,20,40,80,
96,112,128,144,160,176,192,208,224,240.
问题2:它们之间能否交换位置?具有确定的顺序吗?
不能交换位置,并且具有确定的顺序.
记第天月亮可见部分的数为,那么s1=5,s2=10,…,s15=240.
思考:上述的两个例子,有什么共同特征呢?
不能交换位置、具有确定的顺序
新知探究
问题3 的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数
(1)这列数是什么呢?请你列出来;
(2)这列数是否具有上述的特征?如果是,请你仿照以上的叙述,
说明这也是具有确定的顺序的一列数
记第i个数为si,那么s1= ,s2= , s3=, s4=,…
不能交换位置、具有确定的顺序
思考: 上面三个例子的共同特征是什么?
数列的概念:一般地,把按照确定的顺序排列的一列数称为数列.
数列第一个位置上的数叫做这个数列的第1项 (或首项),用符号表示
第二个位置上的数叫做这个数列的第2项, 用符号表示…,
第个位置上的数叫做这个数列的第项, 用符号表示.
数列的一般形式是 : ,简记为.
数列中的每一个数都叫做数列的项.
(1):1,3,5,7是一个数列,7,5,3,1也是一个数列,这两个数列是不是同一个数列?
(2):1,1,1,1,1…是不是一个数列?
概念辨析
项数有限的数列称为有穷数列,如数列1、2;
项数无限的数列称为无穷数列,如数列3.
思考:观察三个例题中的数列的项数有什么区别?
思考: 数列中的每一个数和集合中的元素有什么区别?
1.数列中的数一定是“数”,而集合中的元素不一定是“数”。
2.数列中的数是按一定次序排列的,排列次序不同,那么它们就是不同的数列; 而集合中的元素是无序的。
3.数列定义中并没有规定数列中的数必须不同,同一个数在数列中可以重复出现;而集合中的元素不能重复出现。
数列的一般形式是 : ,简记.
:表示数列
数列中的每一项与它的序号(下标)有下列的对应关系:
序号 1 2 3 … n …
…
…
项
:仅表示数列中的第项这一个数值
概念辨析
思考:在数列中 表示的意义一样吗?为什么?
N*
R
= f(n)
当自变量从1开始,按照从小到大的顺序依次取值时,对应的一列函数值f(1),f(2),…,f(n),…就是数列{}.
另一方面,对于函数,如果f(n) (n∈N*)有意义,那么f(1),f(2),…,f(n),…构成了一个数列{f(n)}。
序号 1 2 3 … n …
…
…
项
数列是自变量为离散的数的函数.
问题4:数列中各项与各项序号之间的对应关系是什么关系?
数列也可以用表格和图象来表示.
思考:从表和图来看,数列中的项随序号的变化呈现出什么特点?
单调性
问题5:类比函数的表示方法,数列还有哪些表示方式?
例如,实例1中王芳身高可以表示表格与图像如下
数列的分类
练习册[例1] 下列数列哪些是有穷数列 哪些是无穷数列 哪些是递增数列 哪些是递减数列 哪些是常数列
(1)1,0.84,0.842,0.843,…;
(2)2,4,6,8,10,…;
(3)7,7,7,7,…;
(5)10,9,8,7,6,5,4,3,2,1;
(6)0,-1,2,-3,4,-5,….
问题6:数列的每一项与它的序号有一定的对应关系,这一关系可否用一个公式表示
如果数列的第项与之间的关系可以用一个公式来表示,
那么这个公式就叫做这个数列的通项公式.
思考: 你能写出例3中 、 、、 ...,数列的通项公式吗?
追问:数列的通项公式有什么作用?
追问:例1、例2中的两个数列也能写成通项公式的形式吗?
实例1:王芳从1岁到17岁每年的身高依次排成一列数:
实例2:在两河流域发掘的一块泥版上就有一列依次表示一个月中
从第1天到第15天每天月亮可见部分的数∶5,10,20,40,80,
96,112,128,144,160,176,192,208,224,240.
并不是所有数列都能写出(或方便写出)其通项公式
例1 根据下列数列{}的通项公式,写出数列的前5项,并画出它们的图象.
(1) ; (2).
解:(1)当通项公式中的n=1,2,3,4,5时,数列{}的前5项依次为1,3,6,10,15. 图象如图 (1)所示.
(2)当通项公式中的n=1,2,3,4,5时,数列{}的前5项依次为1,0,1,0,1. 图象如图 (2)所示.
例2 根据下列数列的前几项,写出数列的个通项公式:
(1) ; (2) ,
(2)观察可知,各项都可以化为分母为2,分子为对应项数的平方的形式,∴该数列的一个通项公式为
解(1):∵,,,
,,,
∴该数列的一个通项公式为.
(3) (4)
(4)∵数列9,99,999,9999,的一个通项公式是
.
解(3):数列的符号规律是正、负相间,使各项分子为4,数列变为
再把各分母分别加上1,数列又变为 ,∴.
例2 根据下列数列的前几项,写出数列的个通项公式:
(1) ; (2) ,
(3) (4)
追问:此数列还可以表示成其他形式吗?
问题7:通过上述实例的研究,你对数列通项公式有什么样的认识
3.数列的通项公式具有双重身份,它表示了数列的第n项,又是这个数列中所有各项的一般表示.
1.并不是所有数列都能写出(或方便写出)其通项公式
2.数列的通项公式的形式不唯一
它反映了一个数列项{}与项数的一种对应关系(函数关系)
数列 通项公式
1,2,3,4,…
1,3,5,7,…
2,4,6,8,…
1,4,9,16,…
1,2,4,8,…
-1,1,-1,1,…
9,99,999,9999,…
1,,,,…
1.数列的定义;
2.数列的通项公式:
(1)定义:用来表示数列的第项与n之间关系的公式
(2)通项公式的理解∶不是所有的数列都有通项公式;
同一个数列可以有不同的通项公式.
3.数列的表示方法:通项公式法、列表法、图象法.
课堂小结
4.1.1 数列的概念与通项
1.能准确说出数列的概念及其表示方法(重点、难点)
2.会用通项公式写出数列的任意一项
3.对于比较简单的数列,会根据给定的前几项写出它的一个通项公式(易错点)
传说古希腊毕达哥拉斯学派的数学家喜欢在沙滩上研究数学问题. 把数描绘成沙滩上的小石子,小石子能摆成不同的几何图形, 就产生了一系列的形数.
他们发现,当小石子的数目是1,3,6,10等数时,小石子都能摆成正三角形,如图(a),他们把这些数叫做三角形数;
当小石子的数目是1,4,9,16等数时,小石子都能摆成正方形,如图(b),他们把这些数叫做正方形数;等等.
实例1:王芳从1岁到17岁每年的身高依次排成一列数:
问题1 :它们之间能否交换位置?具有确定的顺序吗?
第1年
第2年
第3年
.......
不能交换位置,并且具有确定的顺序.
记王芳第i岁时的身高为,则有:
新知探究
实例2:在两河流域发掘的一块泥版上就有一列依次表示一个月中
从第1天到第15天每天月亮可见部分的数∶5,10,20,40,80,
96,112,128,144,160,176,192,208,224,240.
问题2:它们之间能否交换位置?具有确定的顺序吗?
不能交换位置,并且具有确定的顺序.
记第天月亮可见部分的数为,那么s1=5,s2=10,…,s15=240.
思考:上述的两个例子,有什么共同特征呢?
不能交换位置、具有确定的顺序
新知探究
问题3 的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数
(1)这列数是什么呢?请你列出来;
(2)这列数是否具有上述的特征?如果是,请你仿照以上的叙述,
说明这也是具有确定的顺序的一列数
记第i个数为si,那么s1= ,s2= , s3=, s4=,…
不能交换位置、具有确定的顺序
思考: 上面三个例子的共同特征是什么?
数列的概念:一般地,把按照确定的顺序排列的一列数称为数列.
数列第一个位置上的数叫做这个数列的第1项 (或首项),用符号表示
第二个位置上的数叫做这个数列的第2项, 用符号表示…,
第个位置上的数叫做这个数列的第项, 用符号表示.
数列的一般形式是 : ,简记为.
数列中的每一个数都叫做数列的项.
(1):1,3,5,7是一个数列,7,5,3,1也是一个数列,这两个数列是不是同一个数列?
(2):1,1,1,1,1…是不是一个数列?
概念辨析
项数有限的数列称为有穷数列,如数列1、2;
项数无限的数列称为无穷数列,如数列3.
思考:观察三个例题中的数列的项数有什么区别?
思考: 数列中的每一个数和集合中的元素有什么区别?
1.数列中的数一定是“数”,而集合中的元素不一定是“数”。
2.数列中的数是按一定次序排列的,排列次序不同,那么它们就是不同的数列; 而集合中的元素是无序的。
3.数列定义中并没有规定数列中的数必须不同,同一个数在数列中可以重复出现;而集合中的元素不能重复出现。
数列的一般形式是 : ,简记.
:表示数列
数列中的每一项与它的序号(下标)有下列的对应关系:
序号 1 2 3 … n …
…
…
项
:仅表示数列中的第项这一个数值
概念辨析
思考:在数列中 表示的意义一样吗?为什么?
N*
R
= f(n)
当自变量从1开始,按照从小到大的顺序依次取值时,对应的一列函数值f(1),f(2),…,f(n),…就是数列{}.
另一方面,对于函数,如果f(n) (n∈N*)有意义,那么f(1),f(2),…,f(n),…构成了一个数列{f(n)}。
序号 1 2 3 … n …
…
…
项
数列是自变量为离散的数的函数.
问题4:数列中各项与各项序号之间的对应关系是什么关系?
数列也可以用表格和图象来表示.
思考:从表和图来看,数列中的项随序号的变化呈现出什么特点?
单调性
问题5:类比函数的表示方法,数列还有哪些表示方式?
例如,实例1中王芳身高可以表示表格与图像如下
数列的分类
练习册[例1] 下列数列哪些是有穷数列 哪些是无穷数列 哪些是递增数列 哪些是递减数列 哪些是常数列
(1)1,0.84,0.842,0.843,…;
(2)2,4,6,8,10,…;
(3)7,7,7,7,…;
(5)10,9,8,7,6,5,4,3,2,1;
(6)0,-1,2,-3,4,-5,….
问题6:数列的每一项与它的序号有一定的对应关系,这一关系可否用一个公式表示
如果数列的第项与之间的关系可以用一个公式来表示,
那么这个公式就叫做这个数列的通项公式.
思考: 你能写出例3中 、 、、 ...,数列的通项公式吗?
追问:数列的通项公式有什么作用?
追问:例1、例2中的两个数列也能写成通项公式的形式吗?
实例1:王芳从1岁到17岁每年的身高依次排成一列数:
实例2:在两河流域发掘的一块泥版上就有一列依次表示一个月中
从第1天到第15天每天月亮可见部分的数∶5,10,20,40,80,
96,112,128,144,160,176,192,208,224,240.
并不是所有数列都能写出(或方便写出)其通项公式
例1 根据下列数列{}的通项公式,写出数列的前5项,并画出它们的图象.
(1) ; (2).
解:(1)当通项公式中的n=1,2,3,4,5时,数列{}的前5项依次为1,3,6,10,15. 图象如图 (1)所示.
(2)当通项公式中的n=1,2,3,4,5时,数列{}的前5项依次为1,0,1,0,1. 图象如图 (2)所示.
例2 根据下列数列的前几项,写出数列的个通项公式:
(1) ; (2) ,
(2)观察可知,各项都可以化为分母为2,分子为对应项数的平方的形式,∴该数列的一个通项公式为
解(1):∵,,,
,,,
∴该数列的一个通项公式为.
(3) (4)
(4)∵数列9,99,999,9999,的一个通项公式是
.
解(3):数列的符号规律是正、负相间,使各项分子为4,数列变为
再把各分母分别加上1,数列又变为 ,∴.
例2 根据下列数列的前几项,写出数列的个通项公式:
(1) ; (2) ,
(3) (4)
追问:此数列还可以表示成其他形式吗?
问题7:通过上述实例的研究,你对数列通项公式有什么样的认识
3.数列的通项公式具有双重身份,它表示了数列的第n项,又是这个数列中所有各项的一般表示.
1.并不是所有数列都能写出(或方便写出)其通项公式
2.数列的通项公式的形式不唯一
它反映了一个数列项{}与项数的一种对应关系(函数关系)
数列 通项公式
1,2,3,4,…
1,3,5,7,…
2,4,6,8,…
1,4,9,16,…
1,2,4,8,…
-1,1,-1,1,…
9,99,999,9999,…
1,,,,…
1.数列的定义;
2.数列的通项公式:
(1)定义:用来表示数列的第项与n之间关系的公式
(2)通项公式的理解∶不是所有的数列都有通项公式;
同一个数列可以有不同的通项公式.
3.数列的表示方法:通项公式法、列表法、图象法.
课堂小结
