3.4 实际问题与一元一次方程第4课时分段计费和方案问题 课件(共27张PPT)【2023秋人教七上数学高效实用备课】
文档属性
| 名称 | 3.4 实际问题与一元一次方程第4课时分段计费和方案问题 课件(共27张PPT)【2023秋人教七上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 04:31:31 | ||
图片预览






文档简介
(共27张PPT)
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第4课时
分段计费和方案问题
第4节 实际问题与一元一次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
学习目标
重点
难点
1. 体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
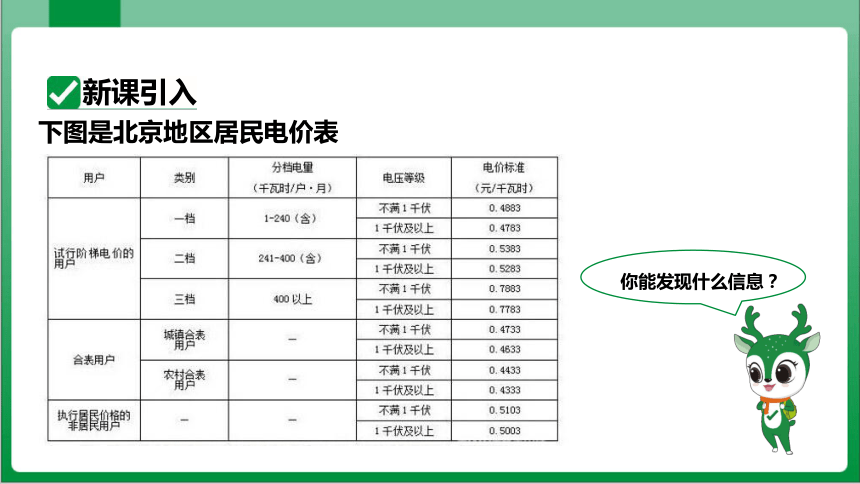
下图是北京地区居民电价表
你能发现什么信息?
新课引入
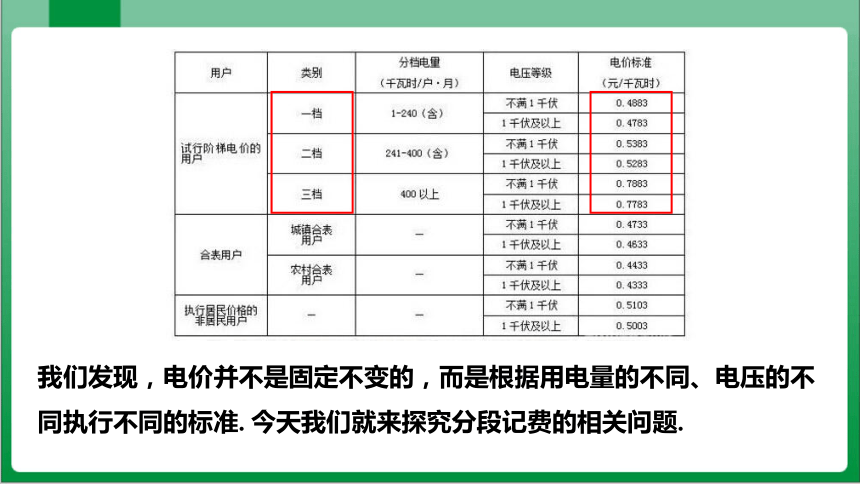
我们发现,电价并不是固定不变的,而是根据用电量的不同、电压的不同执行不同的标准. 今天我们就来探究分段记费的相关问题.
例1 电话计费问题
新知学习
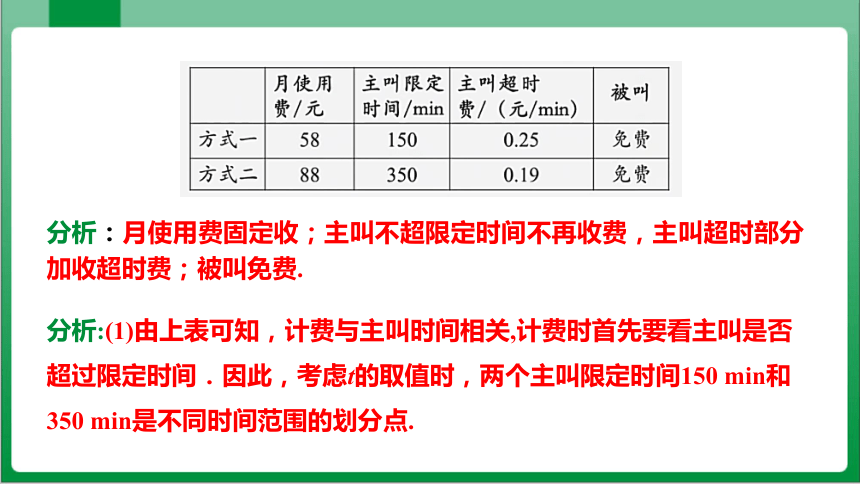
下表中有两种移动电话计费方式
考虑下列问题:
1. 设一个月内用移动电话主叫时间为 t min (t 是正整数). 根据上表,列表说明,当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
2. 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
分析:月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
分析:(1)由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间.因此,考虑t的取值时,两个主叫限定时间150 min和350 min是不同时间范围的划分点.
当t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间 t/min 方式一计费/元 方式二计费/元
t 小于150
t = 150
t 大于150且小于350
t = 350
t 大于350
58
58
58 + 0.25(t - 150)
58 + 0.25(350 - 150)=108
58 + 0.25(t - 150)
88
88
88
88
88 + 0.19(t - 350)
2. 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.下面比较不同时间范围内方式一和方式二的计费情况.
主叫时间 t/min 方式一计费/元 方式二计费/元
t 小于150
t = 150
58
58
88
88
当 t ≤150时,按方式一的计费少.
主叫时间 t/min 方式一计费/元 方式二计费/元
t 大于150且小于350
58 + 0.25(t - 150)
88
当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元.因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等.列方程
58+0.25(t-150)=88,
解得 t=270.
因此,如果主叫时间恰是270 min,按两种方式的计费相等,都是88元;
如果主叫时间大于 150 min 且小于 270 min 时,按方式一的计费少于按方式二的计费(88元);
如果主叫时间大于 270 min 且小于 350 min 时,按方式一的计费多于按方式二的计费(88元).
主叫时间 t/min 方式一计费/元 方式二计费/元
t 大于1t = 350
58 + 0.25(350 - 150)=108
88
当 t =350时,按方式二的计费少.
主叫时间 t/min 方式一计费/元 方式二计费/元
t 大于 350
58 + 0.25(t - 150)
88 + 0.19(t - 350)
当t大于350时,可以看出,按方式一的计费为108元加上超过350 min部分的超时费(0.25(t—350)),按方式二的计费为88元加上超过350 min部分的超时费(0.19(t-350)),按方式二的计费少.
综合以上的分析,可以发现:
t < 270 时,选择方式一省钱;
t = 270 时,两种方式的计费相等,都是88元;
t > 270 时,选择方式二省钱.
归纳
解决分段计费问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
随堂练习
1.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1 500元,乙种电视机每台2 100元,丙种电视机每台2 500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1) 请你设计进货方案;
解:(1) 分三种情况讨论:
①当购进甲、乙两种型号的电视机时,
设购进甲种电视机 x 台,则购进乙种电视机(50-x)台.
根据题意列方程,得
1500x+2 100(50-x)=90 000,
解得 x=25,
50-x=25.
②当购进乙、丙两种型号的电视机时,
设购进乙种电视机 y 台,则购进丙种电视机(50-y)台.
根据题意列方程,得
2 100y+2 500(50-y)=90 000,
解得 y=87.5(不合题意,舍去).
③当购进甲、丙两种型号的电视机时,
设购进甲种电视机 z 台,则购进丙种电视机(50-z)台.
根据题意列方程,得
1 500z+2 500(50-z)=90 000,
解得 z=35,
50-z=15.
所以有以下两种方案:
方案一:购进甲、乙两种型号的电视机各25台.
方案二:购进甲种电视机35台,丙种电视机15台.
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售获利最多,则该选择哪种进货方案.
解:(2) 因为商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,
所以方案一的利润为 150×25+200×25=8 750(元),
方案二的利润为 150×35+250×15=9 000(元).
因为8 750<9 000,
所以选择方案二获利最多.
答:为使销售获利最多,应该选择购进甲种电视机35台,丙种电视机15台的进货方案.
课堂小结
解决分段计费问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第4课时
分段计费和方案问题
第4节 实际问题与一元一次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
学习目标
重点
难点
1. 体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
下图是北京地区居民电价表
你能发现什么信息?
新课引入
我们发现,电价并不是固定不变的,而是根据用电量的不同、电压的不同执行不同的标准. 今天我们就来探究分段记费的相关问题.
例1 电话计费问题
新知学习
下表中有两种移动电话计费方式
考虑下列问题:
1. 设一个月内用移动电话主叫时间为 t min (t 是正整数). 根据上表,列表说明,当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
2. 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
分析:月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
分析:(1)由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间.因此,考虑t的取值时,两个主叫限定时间150 min和350 min是不同时间范围的划分点.
当t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间 t/min 方式一计费/元 方式二计费/元
t 小于150
t = 150
t 大于150且小于350
t = 350
t 大于350
58
58
58 + 0.25(t - 150)
58 + 0.25(350 - 150)=108
58 + 0.25(t - 150)
88
88
88
88
88 + 0.19(t - 350)
2. 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.下面比较不同时间范围内方式一和方式二的计费情况.
主叫时间 t/min 方式一计费/元 方式二计费/元
t 小于150
t = 150
58
58
88
88
当 t ≤150时,按方式一的计费少.
主叫时间 t/min 方式一计费/元 方式二计费/元
t 大于150且小于350
58 + 0.25(t - 150)
88
当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元.因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等.列方程
58+0.25(t-150)=88,
解得 t=270.
因此,如果主叫时间恰是270 min,按两种方式的计费相等,都是88元;
如果主叫时间大于 150 min 且小于 270 min 时,按方式一的计费少于按方式二的计费(88元);
如果主叫时间大于 270 min 且小于 350 min 时,按方式一的计费多于按方式二的计费(88元).
主叫时间 t/min 方式一计费/元 方式二计费/元
t 大于1t = 350
58 + 0.25(350 - 150)=108
88
当 t =350时,按方式二的计费少.
主叫时间 t/min 方式一计费/元 方式二计费/元
t 大于 350
58 + 0.25(t - 150)
88 + 0.19(t - 350)
当t大于350时,可以看出,按方式一的计费为108元加上超过350 min部分的超时费(0.25(t—350)),按方式二的计费为88元加上超过350 min部分的超时费(0.19(t-350)),按方式二的计费少.
综合以上的分析,可以发现:
t < 270 时,选择方式一省钱;
t = 270 时,两种方式的计费相等,都是88元;
t > 270 时,选择方式二省钱.
归纳
解决分段计费问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
随堂练习
1.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1 500元,乙种电视机每台2 100元,丙种电视机每台2 500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1) 请你设计进货方案;
解:(1) 分三种情况讨论:
①当购进甲、乙两种型号的电视机时,
设购进甲种电视机 x 台,则购进乙种电视机(50-x)台.
根据题意列方程,得
1500x+2 100(50-x)=90 000,
解得 x=25,
50-x=25.
②当购进乙、丙两种型号的电视机时,
设购进乙种电视机 y 台,则购进丙种电视机(50-y)台.
根据题意列方程,得
2 100y+2 500(50-y)=90 000,
解得 y=87.5(不合题意,舍去).
③当购进甲、丙两种型号的电视机时,
设购进甲种电视机 z 台,则购进丙种电视机(50-z)台.
根据题意列方程,得
1 500z+2 500(50-z)=90 000,
解得 z=35,
50-z=15.
所以有以下两种方案:
方案一:购进甲、乙两种型号的电视机各25台.
方案二:购进甲种电视机35台,丙种电视机15台.
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售获利最多,则该选择哪种进货方案.
解:(2) 因为商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,
所以方案一的利润为 150×25+200×25=8 750(元),
方案二的利润为 150×35+250×15=9 000(元).
因为8 750<9 000,
所以选择方案二获利最多.
答:为使销售获利最多,应该选择购进甲种电视机35台,丙种电视机15台的进货方案.
课堂小结
解决分段计费问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
