3.4 实际问题与一元一次方程第3课时比赛积分和行程问题 课件(共29张PPT)【2023秋人教七上数学高效实用备课】
文档属性
| 名称 | 3.4 实际问题与一元一次方程第3课时比赛积分和行程问题 课件(共29张PPT)【2023秋人教七上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第3课时
比赛积分和行程问题
第4节 实际问题与一元一次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 会阅读,理解表格,并从表格中提取信息;
2. 会运用方程解决比赛积分问题;
3. 理解行程问题中常见的数量关系,会运用方程解决行程问题.
学习目标
重点
难点
重点
重点
2021/2022 英超正式收官,曼城逆转战胜维拉以 1 分的优势夺冠,红军、切尔西、热刺分获 2 - 4 位,阿森纳、曼联则是分获第五、第六位.
新课引入
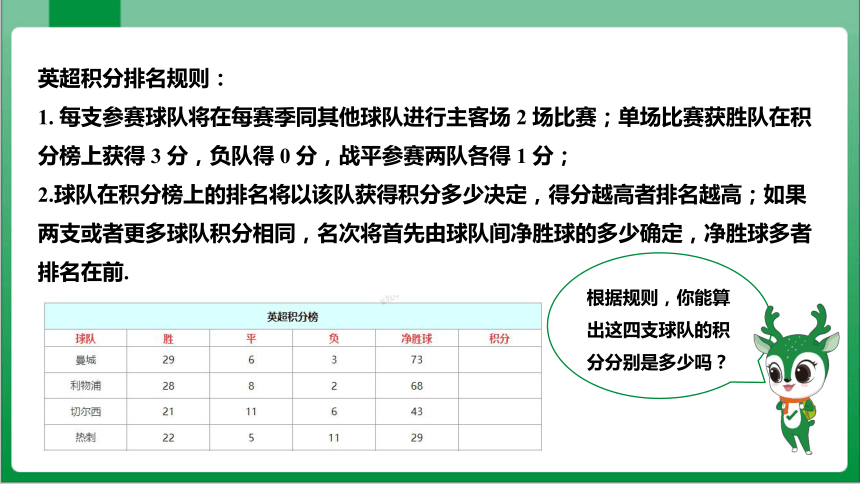
英超积分排名规则:
1. 每支参赛球队将在每赛季同其他球队进行主客场 2 场比赛;单场比赛获胜队在积分榜上获得 3 分,负队得 0 分,战平参赛两队各得 1 分;
2.球队在积分榜上的排名将以该队获得积分多少决定,得分越高者排名越高;如果两支或者更多球队积分相同,名次将首先由球队间净胜球的多少确定,净胜球多者排名在前.
根据规则,你能算出这四支球队的积分分别是多少吗?
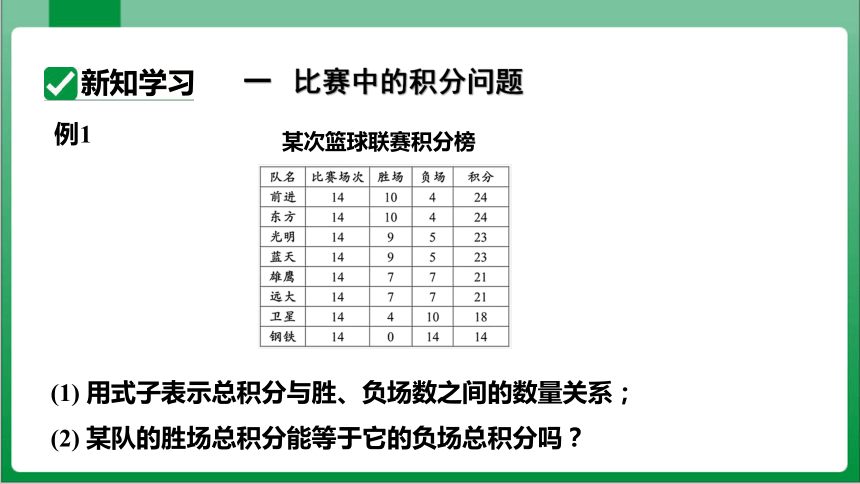
例1
(1) 用式子表示总积分与胜、负场数之间的数量关系;
(2) 某队的胜场总积分能等于它的负场总积分吗?
新知学习
一 比赛中的积分问题
某次篮球联赛积分榜
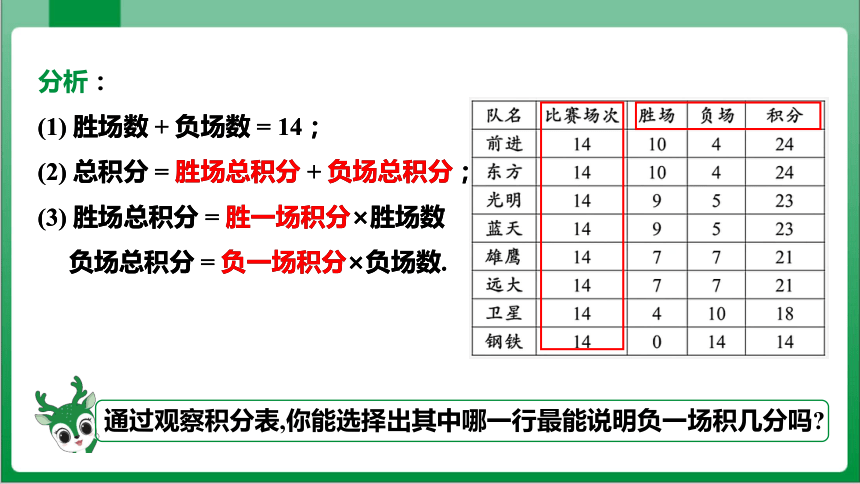
分析:
(1) 胜场数 + 负场数 = 14;
(2) 总积分 = 胜场总积分 + 负场总积分;
(3) 胜场总积分 = 胜一场积分×胜场数
负场总积分 = 负一场积分×负场数.
(1) 胜场数 + 负场数 = 14;
(2) 总积分 = 胜场总积分 + 负场总积分;
(3) 胜场总积分 = 胜一场积分×胜场数
负场总积分 = 负一场积分×负场数.
通过观察积分表,你能选择出其中哪一行最能说明负一场积几分吗
分析:观察积分榜,从最下面一行数据可以看出:负一场积1分.
队名 比赛场次 胜场 负场 积分
钢铁 14 0 14 14
设胜一场积x分,从表中其他任何一行可以列方程,求出x的值,例如,从第一行得方程
10x+1×4=24.
由此得 x=2.
用积分榜中其他行可以验证,得出结论:负一场积1分,胜一场积2分.
(1)分析:设某队胜 m 场,则负 (14 - m) 场.
胜场总积分 负场总积分 胜一场积分 负一场积分
2m (14 - m) 2 1
解:如果一个队胜 m 场,则负(14 - m)场.
胜场总积分为 2m,负场总积分为 14 - m,总积分为:
2m + (14 - m) = m + 14.
(2) 某队的胜场总积分能等于它的负场总积分吗?
解:设一个队胜 x 场,则负 (14 - x) 场.
如果这个队的胜场总积分等于负场总积分,
则得方程 2x = 14 - x.
由此,得 x = .
检验,x = 是原方程的解但不符合实际意义.
答:没有哪个队的胜场总积分可以等于它的负场总积分.
x表示什么量 它可以是分数吗
x表示某队获胜的场数,它应是自然数,不能是分数.
归纳
这个问题说明:利用方程不仅能求具体数值,而且可以进行推理判断.
用方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.
比赛积分问题中常见的等量关系:
某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;
某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.
二 行程问题
例2 “甲、乙两人,同时出发,相对而行,距离是50km,甲每小时走3 km ,乙每小时走2km,问他俩几小时后相距40 km ?”
分情况讨论:
(1)相遇前距离40 km:
甲的路程 +乙的路程+40 km =总路程
(2)相遇后距离40 km:
甲的路程 +乙的路程-40 km =总路程
A
B
s甲
s乙
40km
A
B
s甲
s乙
40km
解:(1)相遇前相距40 km
设x小时后相距 40 km,根据题意得
3x + 2x + 40 = 50
解方程,得 x= 2
(2)相遇后相距40 km
设y小 时后相距 40 km,根据题意得
3y + 2y – 40 = 50
解方程,得 x= 18
综上所述,2小时或18小时后相距 40 km.
例3 船从甲地顺水开往乙地,所用时间比从乙地逆水开往甲地少1.5小时.已知船在静水的速度为18千米/小时,水流速度为2千米/小时,求甲、乙两地之间的距离?
分析:顺水速度=船速+水速;
逆水速度=船速-水速.
解 设船逆水航行从乙地到甲地需x小时,依题意,得:
(18+2)(x -1.5)= (18 -2)x
解方程,得:x=7.5
(18 -2) ×7.5=120
答:甲、乙两地距离为120千米.
行程问题中常见的等量关系:
路程=速度×时间;
相遇问题:总路程=甲走的路程+乙走的路程;
航行问题:顺水速度=船速+水速;
逆水速度=船速-水速.
归纳
某电视台组织知识竞赛,共设 20 道选择题,各题分值相同,每题必答. 下表记录了 5 个参赛者的得分情况.
(1) 参赛者 F 得 76 分,他答对了几道题?
(2) 参赛者 G 说他得 80 分,你认为可能吗?为什么?
随堂练习
分析:
(1) 答对题数 + 答错题数 = 20;
(2) 答对题得分 + 答错题得分 = 总得分;
(3) 答对题得分 = 答对题数×对一题得分
答错题得分 = 答错题数×错一题得分.
想一想:哪些未知量是可以通过表格信息求出来的?
(1) 答对题数 + 答错题数 = 20;
(2) 答对题得分 + 答错题得分 = 总得分;
(3) 答对题得分 = 答对题数×对一题得分
答错题得分 = 答错题数×错一题得分.
分析:观察积分榜,从第一行数据可以看出:答对一题得5分.
设答错一题得x分,从表中其他任何一行可以列方程,求出x的值,例如,从最后一行得方程
10x+10×5=40.
由此得 x=-1.
用得分榜中其他行可以验证,得出结论:答对一题得5分,答错一题得-1分.
(1) 参赛者 F 得 76 分,他答对了几道题?
解:设 F 答对了 x 道题,则答错了 (20 - x) 道题.
列方程,得
5x + (-1)×(20-x) = 76.
解得 x = 16.
检验:x = 16 是原方程的解且符合实际意义.
答:他答对了 16 道题.
(2) 参赛者 G 说他得 80 分,你认为可能吗?为什么?
解:设 G 答对了 m 道题,则答错了 (20 - m) 道题.
假设 G 得 80 分,可列方程
5m + (-1)×(20 - m) = 80.
m = .
检验:m = 是原方程的解但不符合实际意义.
答:参赛者 G 不可能得 80 分.
2.小李和爸爸周末去体育中心晨练,两人沿400 m 的跑道匀速跑步,每次总是小李跑了2 圈爸爸跑3 圈,一次两人在同地反向而跑,小李最后发现隔了32 s 两人第一次相遇.求两人的速度.
分析:设小李的速度为2x米/秒,则爸爸的速度为3x米/秒.
根据等量关系:相遇时间×两人的速度和=400米,列出方程即可;
解:设小李的速度为2x米/秒,则爸爸的速度为3x米/秒.根据题意,得:
32(2x+3x)=400,
解方程,得 x=2.5,
2x=5,
3x=7.5.
答:小李的速度为5米/秒,爸爸的速度为7.5米/秒;
课堂小结
1.比赛积分问题中常见的等量关系:
某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;
某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.
2.行程问题中常见的等量关系:
路程=速度×时间;
相遇问题:总路程=甲走的路程+乙走的路程;
航行问题:顺水速度=船速+水速;
逆水速度=船速-水速.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第3课时
比赛积分和行程问题
第4节 实际问题与一元一次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 会阅读,理解表格,并从表格中提取信息;
2. 会运用方程解决比赛积分问题;
3. 理解行程问题中常见的数量关系,会运用方程解决行程问题.
学习目标
重点
难点
重点
重点
2021/2022 英超正式收官,曼城逆转战胜维拉以 1 分的优势夺冠,红军、切尔西、热刺分获 2 - 4 位,阿森纳、曼联则是分获第五、第六位.
新课引入
英超积分排名规则:
1. 每支参赛球队将在每赛季同其他球队进行主客场 2 场比赛;单场比赛获胜队在积分榜上获得 3 分,负队得 0 分,战平参赛两队各得 1 分;
2.球队在积分榜上的排名将以该队获得积分多少决定,得分越高者排名越高;如果两支或者更多球队积分相同,名次将首先由球队间净胜球的多少确定,净胜球多者排名在前.
根据规则,你能算出这四支球队的积分分别是多少吗?
例1
(1) 用式子表示总积分与胜、负场数之间的数量关系;
(2) 某队的胜场总积分能等于它的负场总积分吗?
新知学习
一 比赛中的积分问题
某次篮球联赛积分榜
分析:
(1) 胜场数 + 负场数 = 14;
(2) 总积分 = 胜场总积分 + 负场总积分;
(3) 胜场总积分 = 胜一场积分×胜场数
负场总积分 = 负一场积分×负场数.
(1) 胜场数 + 负场数 = 14;
(2) 总积分 = 胜场总积分 + 负场总积分;
(3) 胜场总积分 = 胜一场积分×胜场数
负场总积分 = 负一场积分×负场数.
通过观察积分表,你能选择出其中哪一行最能说明负一场积几分吗
分析:观察积分榜,从最下面一行数据可以看出:负一场积1分.
队名 比赛场次 胜场 负场 积分
钢铁 14 0 14 14
设胜一场积x分,从表中其他任何一行可以列方程,求出x的值,例如,从第一行得方程
10x+1×4=24.
由此得 x=2.
用积分榜中其他行可以验证,得出结论:负一场积1分,胜一场积2分.
(1)分析:设某队胜 m 场,则负 (14 - m) 场.
胜场总积分 负场总积分 胜一场积分 负一场积分
2m (14 - m) 2 1
解:如果一个队胜 m 场,则负(14 - m)场.
胜场总积分为 2m,负场总积分为 14 - m,总积分为:
2m + (14 - m) = m + 14.
(2) 某队的胜场总积分能等于它的负场总积分吗?
解:设一个队胜 x 场,则负 (14 - x) 场.
如果这个队的胜场总积分等于负场总积分,
则得方程 2x = 14 - x.
由此,得 x = .
检验,x = 是原方程的解但不符合实际意义.
答:没有哪个队的胜场总积分可以等于它的负场总积分.
x表示什么量 它可以是分数吗
x表示某队获胜的场数,它应是自然数,不能是分数.
归纳
这个问题说明:利用方程不仅能求具体数值,而且可以进行推理判断.
用方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.
比赛积分问题中常见的等量关系:
某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;
某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.
二 行程问题
例2 “甲、乙两人,同时出发,相对而行,距离是50km,甲每小时走3 km ,乙每小时走2km,问他俩几小时后相距40 km ?”
分情况讨论:
(1)相遇前距离40 km:
甲的路程 +乙的路程+40 km =总路程
(2)相遇后距离40 km:
甲的路程 +乙的路程-40 km =总路程
A
B
s甲
s乙
40km
A
B
s甲
s乙
40km
解:(1)相遇前相距40 km
设x小时后相距 40 km,根据题意得
3x + 2x + 40 = 50
解方程,得 x= 2
(2)相遇后相距40 km
设y小 时后相距 40 km,根据题意得
3y + 2y – 40 = 50
解方程,得 x= 18
综上所述,2小时或18小时后相距 40 km.
例3 船从甲地顺水开往乙地,所用时间比从乙地逆水开往甲地少1.5小时.已知船在静水的速度为18千米/小时,水流速度为2千米/小时,求甲、乙两地之间的距离?
分析:顺水速度=船速+水速;
逆水速度=船速-水速.
解 设船逆水航行从乙地到甲地需x小时,依题意,得:
(18+2)(x -1.5)= (18 -2)x
解方程,得:x=7.5
(18 -2) ×7.5=120
答:甲、乙两地距离为120千米.
行程问题中常见的等量关系:
路程=速度×时间;
相遇问题:总路程=甲走的路程+乙走的路程;
航行问题:顺水速度=船速+水速;
逆水速度=船速-水速.
归纳
某电视台组织知识竞赛,共设 20 道选择题,各题分值相同,每题必答. 下表记录了 5 个参赛者的得分情况.
(1) 参赛者 F 得 76 分,他答对了几道题?
(2) 参赛者 G 说他得 80 分,你认为可能吗?为什么?
随堂练习
分析:
(1) 答对题数 + 答错题数 = 20;
(2) 答对题得分 + 答错题得分 = 总得分;
(3) 答对题得分 = 答对题数×对一题得分
答错题得分 = 答错题数×错一题得分.
想一想:哪些未知量是可以通过表格信息求出来的?
(1) 答对题数 + 答错题数 = 20;
(2) 答对题得分 + 答错题得分 = 总得分;
(3) 答对题得分 = 答对题数×对一题得分
答错题得分 = 答错题数×错一题得分.
分析:观察积分榜,从第一行数据可以看出:答对一题得5分.
设答错一题得x分,从表中其他任何一行可以列方程,求出x的值,例如,从最后一行得方程
10x+10×5=40.
由此得 x=-1.
用得分榜中其他行可以验证,得出结论:答对一题得5分,答错一题得-1分.
(1) 参赛者 F 得 76 分,他答对了几道题?
解:设 F 答对了 x 道题,则答错了 (20 - x) 道题.
列方程,得
5x + (-1)×(20-x) = 76.
解得 x = 16.
检验:x = 16 是原方程的解且符合实际意义.
答:他答对了 16 道题.
(2) 参赛者 G 说他得 80 分,你认为可能吗?为什么?
解:设 G 答对了 m 道题,则答错了 (20 - m) 道题.
假设 G 得 80 分,可列方程
5m + (-1)×(20 - m) = 80.
m = .
检验:m = 是原方程的解但不符合实际意义.
答:参赛者 G 不可能得 80 分.
2.小李和爸爸周末去体育中心晨练,两人沿400 m 的跑道匀速跑步,每次总是小李跑了2 圈爸爸跑3 圈,一次两人在同地反向而跑,小李最后发现隔了32 s 两人第一次相遇.求两人的速度.
分析:设小李的速度为2x米/秒,则爸爸的速度为3x米/秒.
根据等量关系:相遇时间×两人的速度和=400米,列出方程即可;
解:设小李的速度为2x米/秒,则爸爸的速度为3x米/秒.根据题意,得:
32(2x+3x)=400,
解方程,得 x=2.5,
2x=5,
3x=7.5.
答:小李的速度为5米/秒,爸爸的速度为7.5米/秒;
课堂小结
1.比赛积分问题中常见的等量关系:
某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;
某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.
2.行程问题中常见的等量关系:
路程=速度×时间;
相遇问题:总路程=甲走的路程+乙走的路程;
航行问题:顺水速度=船速+水速;
逆水速度=船速-水速.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
