5.4.2 圆周角和直径的关系同步练习(含答案)
文档属性
| 名称 | 5.4.2 圆周角和直径的关系同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 20:53:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
4 圆周角和圆心角的关系
第2课时 圆周角和直径的关系
基础闯关
知识点:圆周角定理的推论3
命题角度1:直径所对的圆周角是直角
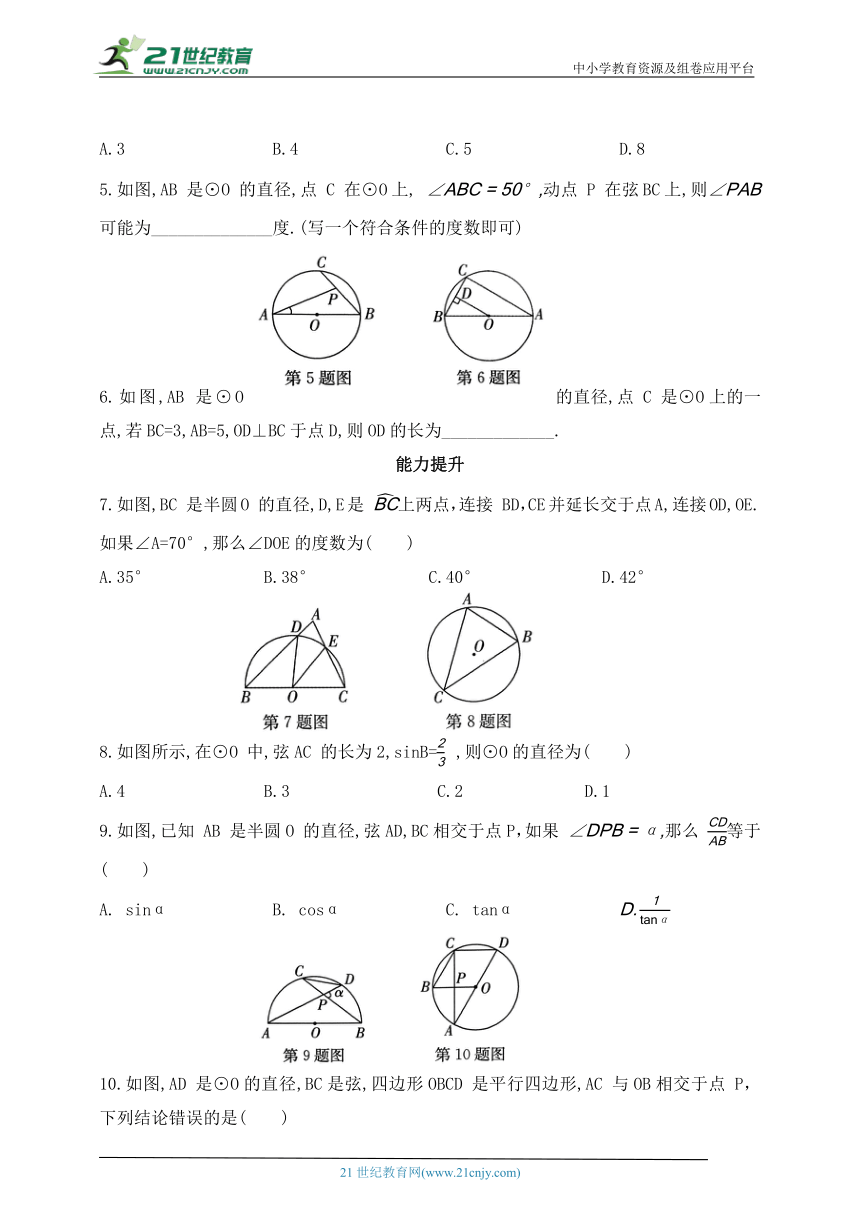
1.如图,AB 是⊙O 的直径,若 则∠ADC=( )
A.32° B.58° C.62° D.116°
2.如图所示,AB是⊙O 的直径,弦CD∥AB.若∠ABD=65°,则∠ADC=___________.
命题角度2:90°的圆周角所对的弦是直径
3.(1)如图①,把直角三角尺的直角顶点O放在破损的圆形玻璃镜的圆周上,两直角边与圆弧分别交于点 M,N,量得OM=8cm,ON=6cm,则该圆形玻璃镜的半径是( )
(2)在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径,如图②,∠AOB=90°,将点O放在圆周上,分别确定OA,OB 与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )
A.17 B.14 C.12 D.10
命题角度3:利用直径和圆周角的关系进行计算
4.如图,在平面直角坐标系中,⊙A 经过原点O,并且分别与x 轴、y 轴交于B,C 两点,已知B(8,0),C(0,6),则⊙A 的半径为( )
A.3 B.4 C.5 D.8
5.如图,AB 是⊙O 的直径,点 C 在⊙O上, 动点 P 在弦BC上,则可能为______________度.(写一个符合条件的度数即可)
6.如图,AB 是⊙O 的直径,点 C 是⊙O上的一点,若BC=3,AB=5,OD⊥BC于点D,则OD的长为_____________.
能力提升
7.如图,BC 是半圆O 的直径,D,E是 上两点,连接 BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )
A.35° B.38° C.40° D.42°
8.如图所示,在⊙O 中,弦AC 的长为2,sinB=,则⊙O的直径为( )
A.4 B.3 C.2 D.1
9.如图,已知 AB 是半圆O 的直径,弦AD,BC相交于点P,如果 那么 等于( )
A. sinα B. cosα C. tanα
10.如图,AD 是⊙O的直径,BC是弦,四边形OBCD 是平行四边形,AC 与OB相交于点 P,下列结论错误的是( )
A. AP=2OP B. CD=2OP C. OB⊥AC D. AC 平分OB
11.如图,小杨将一个三角尺放在⊙O上,使三角尺的一直角边经过圆心 O,测得
5cm,AB=3cm,则⊙O 的半径长为( )
A.3cm C.4 cm
12.如图,△ABC 是等边三角形,点 A,B 在数轴上,点A 表示数-2,点B 表示数2,以AB为直径作圆交边 AC 于点P,以 B 为圆心,BP 为半径作弧交数轴于点Q,则点 Q 在数轴上表示的数为( )
13.如图,AB 为⊙O 的直径, BC交⊙O 于点D,AC 交⊙O 于点 E,
(1)求 的度数.
(2)连接ED,若 求ED的长.
培优创新
14.如图,在平面直角坐标系中,O 为坐标原点,P 是反比例函数 图象上任意一点,以P 为圆心,PO长为半径的圆与x轴交于点A,与y 轴交于点B,连接AB.
(1)求证:P 为线段AB 的中点.
(2)求 的面积.
参考答案
1. C 2.25° 3.(1)B (2)C 4. C 5.示例:30 6.2
7. C 8. B 9. B 10. A
11. D [解析]如图,延长CA 交⊙O 于点 D,连接 BC,BD.
∵CD 为直径,
AB,即
的半径长为
12. C [解析]由题意可得 AB=4.∵△ABC 是等边三角形,∴∠BAC=60°.
∵AB 是⊙O 的直径,∴∠APB=90°,
在 Rt△APB中,AB
∵以BP为半径作弧交数轴于点Q,∴BQ=PB=.点 Q 表示的数为
13.解:(1)连接 AD.∵AB是⊙O 的直径,∴∠ADB=90°.
又知AB=AC,∴根据等腰三角形“三线合一”的性质,得∠DAC=22.5°.
(2)由等腰三角形“三线合一”的性质,得 BD=DC.
∵AB 是⊙O 的直径,∴∠AEB=90°,
14.(1)证明:∵点A,O,B在⊙P 上,且∠AOB=90°,∴AB为⊙P 的直径,即 P 为线段AB 的中点.
(2)解:∵P 为 上的点,设点 P 的坐标为(m,n),则mn=12.
如图,过点 P 作PM⊥x 轴于点M,PN⊥y轴于点N,∴点 M 的坐标为(m,0),点 N 的坐标为(0,n),且OM=m,ON=n.易得M为OA 中点,OA=2m,N 为 OB 中点, 2mn=24.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
4 圆周角和圆心角的关系
第2课时 圆周角和直径的关系
基础闯关
知识点:圆周角定理的推论3
命题角度1:直径所对的圆周角是直角
1.如图,AB 是⊙O 的直径,若 则∠ADC=( )
A.32° B.58° C.62° D.116°
2.如图所示,AB是⊙O 的直径,弦CD∥AB.若∠ABD=65°,则∠ADC=___________.
命题角度2:90°的圆周角所对的弦是直径
3.(1)如图①,把直角三角尺的直角顶点O放在破损的圆形玻璃镜的圆周上,两直角边与圆弧分别交于点 M,N,量得OM=8cm,ON=6cm,则该圆形玻璃镜的半径是( )
(2)在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径,如图②,∠AOB=90°,将点O放在圆周上,分别确定OA,OB 与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )
A.17 B.14 C.12 D.10
命题角度3:利用直径和圆周角的关系进行计算
4.如图,在平面直角坐标系中,⊙A 经过原点O,并且分别与x 轴、y 轴交于B,C 两点,已知B(8,0),C(0,6),则⊙A 的半径为( )
A.3 B.4 C.5 D.8
5.如图,AB 是⊙O 的直径,点 C 在⊙O上, 动点 P 在弦BC上,则可能为______________度.(写一个符合条件的度数即可)
6.如图,AB 是⊙O 的直径,点 C 是⊙O上的一点,若BC=3,AB=5,OD⊥BC于点D,则OD的长为_____________.
能力提升
7.如图,BC 是半圆O 的直径,D,E是 上两点,连接 BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )
A.35° B.38° C.40° D.42°
8.如图所示,在⊙O 中,弦AC 的长为2,sinB=,则⊙O的直径为( )
A.4 B.3 C.2 D.1
9.如图,已知 AB 是半圆O 的直径,弦AD,BC相交于点P,如果 那么 等于( )
A. sinα B. cosα C. tanα
10.如图,AD 是⊙O的直径,BC是弦,四边形OBCD 是平行四边形,AC 与OB相交于点 P,下列结论错误的是( )
A. AP=2OP B. CD=2OP C. OB⊥AC D. AC 平分OB
11.如图,小杨将一个三角尺放在⊙O上,使三角尺的一直角边经过圆心 O,测得
5cm,AB=3cm,则⊙O 的半径长为( )
A.3cm C.4 cm
12.如图,△ABC 是等边三角形,点 A,B 在数轴上,点A 表示数-2,点B 表示数2,以AB为直径作圆交边 AC 于点P,以 B 为圆心,BP 为半径作弧交数轴于点Q,则点 Q 在数轴上表示的数为( )
13.如图,AB 为⊙O 的直径, BC交⊙O 于点D,AC 交⊙O 于点 E,
(1)求 的度数.
(2)连接ED,若 求ED的长.
培优创新
14.如图,在平面直角坐标系中,O 为坐标原点,P 是反比例函数 图象上任意一点,以P 为圆心,PO长为半径的圆与x轴交于点A,与y 轴交于点B,连接AB.
(1)求证:P 为线段AB 的中点.
(2)求 的面积.
参考答案
1. C 2.25° 3.(1)B (2)C 4. C 5.示例:30 6.2
7. C 8. B 9. B 10. A
11. D [解析]如图,延长CA 交⊙O 于点 D,连接 BC,BD.
∵CD 为直径,
AB,即
的半径长为
12. C [解析]由题意可得 AB=4.∵△ABC 是等边三角形,∴∠BAC=60°.
∵AB 是⊙O 的直径,∴∠APB=90°,
在 Rt△APB中,AB
∵以BP为半径作弧交数轴于点Q,∴BQ=PB=.点 Q 表示的数为
13.解:(1)连接 AD.∵AB是⊙O 的直径,∴∠ADB=90°.
又知AB=AC,∴根据等腰三角形“三线合一”的性质,得∠DAC=22.5°.
(2)由等腰三角形“三线合一”的性质,得 BD=DC.
∵AB 是⊙O 的直径,∴∠AEB=90°,
14.(1)证明:∵点A,O,B在⊙P 上,且∠AOB=90°,∴AB为⊙P 的直径,即 P 为线段AB 的中点.
(2)解:∵P 为 上的点,设点 P 的坐标为(m,n),则mn=12.
如图,过点 P 作PM⊥x 轴于点M,PN⊥y轴于点N,∴点 M 的坐标为(m,0),点 N 的坐标为(0,n),且OM=m,ON=n.易得M为OA 中点,OA=2m,N 为 OB 中点, 2mn=24.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
