3.3 第1课时解一元一次方程——去括号 课件(共21张PPT)【2023秋人教七上数学高效实用备课】
文档属性
| 名称 | 3.3 第1课时解一元一次方程——去括号 课件(共21张PPT)【2023秋人教七上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 04:43:06 | ||
图片预览








文档简介
(共21张PPT)
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第1课时 去括号
第3节 解一元一次方程(二)
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 了解去括号是方程中常用的化简步骤;
2. 准确熟练地运用去括号法则解带有括号的一元一次方程.
学习目标
重点
新课引入
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
a + (b + c)= a + b + c.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
a - (b + c) = a - b - c.
回顾整式的去括号法则:
新知学习
问题1 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15万 kW·h. 这个工厂去年上半年每月平均用电是多少?
1kW·h的电量即1kW的电器1h的用电量.
设上半年每月平均用电量为x kW·h,
则下半年每月平均用电量为(x-2 000) kW·h.
上半年共用电6x kW·h,
下半年共用电6(x-2 000) kW·h.
根据全年用电15万kW·h,列得方程
6x+6(x -2 000)=150 000.
如果去括号,就能简化方程的形式.
下面的框图表示了解这个方程的流程.
去括号
6x + 6 ( x-2 000 ) = 150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
移项
合并同类项
系数化为1
由上可知,这个工厂去年上半年每月平均用电13500kW·h.
本题还有其他列方程的方法吗?
方程中等号左右两边都是一年中每两个月的平均用电量.
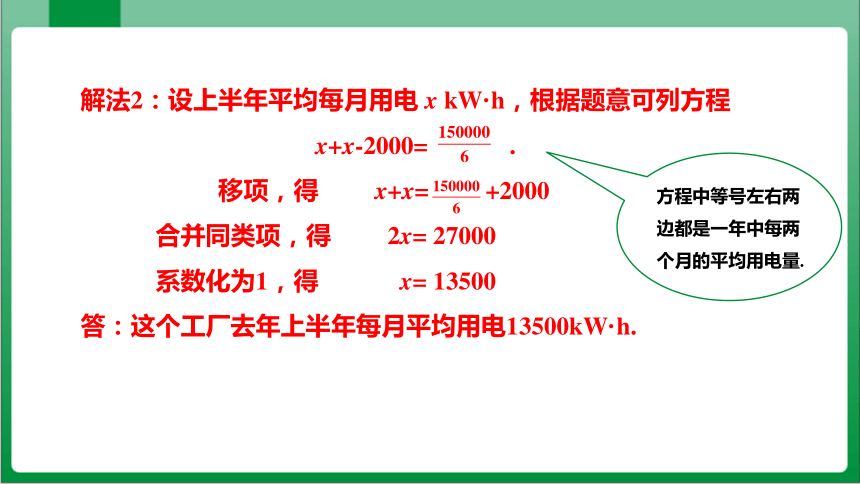
解法2:设上半年平均每月用电 x kW·h,根据题意可列方程
x+x-2000= .
移项,得 x+x= +2000
合并同类项,得 2x= 27000
系数化为1,得 x= 13500
答:这个工厂去年上半年每月平均用电13500kW·h.
例1 解下列方程:
(1) 2x - (x + 10) = 5x + 2(x - 1);
解:去括号,得 2x - x - 10 = 5x + 2x - 2.
移项,得 2x - x - 5x - 2x = -2 + 10.
合并同类项,得 -6x = 8.
系数化为 1,得 .
例1 解下列方程:
(2) 3x - 7(x - 1) = 3 - 2(x + 3);
解:去括号,得 3x - 7x + 7 = 3 - 2x - 6.
移项,得 3x - 7x + 2x = 3 - 6 - 7.
合并同类项,得 -2x = -10.
系数化为 1,得 x = 5.
归纳
解一元一次方程的一般步骤:
(1) 去括号;
(2) 移项;
(3) 合并同类项;
(4) 系数化为 1.
例2 一艘船从甲码头到乙码头顺流而行,用了 2 h;从乙码头返回甲码头逆流而行,用了 2.5 h.已知水流的速度是 3 km/h,求船在静水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间.
×
=
×
解:设船在静水中的平均速度为 x km/h,
则顺流速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得 2x + 6 = 2.5x-7.5.
移项、合并同类项,得 0.5x = 13.5.
系数化为1,得 x = 27.
答:船在静水中的平均速度为 27 km/h.
根据往返路程相等, 列得 2( x+3 ) = 2.5( x-3 ).
1. 解下列方程:
(1) 2(x + 3) = 5x;
解:去括号,得 2x + 6 = 5x.
移项,得 2x - 5x = -6.
合并同类项,得 -3x = -6.
系数化为 1,得 x = 2.
随堂练习
1. 解下列方程:
(2) 4x + 3(2x - 3) = 12 - (x + 4);
解:去括号,得 4x + 6x - 9= 12 – x - 4.
移项,得 4x + 6x + x= 12 – 4 + 9.
合并同类项,得 11x = 17.
系数化为 1,得 x =
1. 解下列方程:
(3) 2 – 3(x + 1) = 1 – 2(1 + 0.5x);
解:去括号,得 2 – 3x – 3 = 1 – 2 – x.
移项, 得 -3x+x = 1 – 2 – 2 + 3.
合并同类项,得 -2x = 0.
系数化为 1,得 x = 0.
2. 一架飞机在两城之间航行,风速为 24 km/h,顺风飞行要 2 小时 50 分,逆风飞行要 3 小时,求两城距离.
解:设飞机在无风时的速度为 x km/h,则在顺风中的速度为 (x+24) km/h ,在逆风中的速度为 (x-24)km/h.根据题意,得
(x+24)=3 (x-24)
去括号,得 x + 68 = 3x-72.
移项, 得 x - 3x = -72-68.
两城市的距离为 3×(840 - 24) = 2448 (km).
答:两城市之间的距离为 2448 km.
合并同类项,得 x = -140.
系数化为 1,得 x = 840.
课堂小结
解一元一次方程的一般步骤:
(1) 去括号;
(2) 移项;
(3) 合并同类项;
(4) 系数化为 1.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第1课时 去括号
第3节 解一元一次方程(二)
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 了解去括号是方程中常用的化简步骤;
2. 准确熟练地运用去括号法则解带有括号的一元一次方程.
学习目标
重点
新课引入
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
a + (b + c)= a + b + c.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
a - (b + c) = a - b - c.
回顾整式的去括号法则:
新知学习
问题1 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15万 kW·h. 这个工厂去年上半年每月平均用电是多少?
1kW·h的电量即1kW的电器1h的用电量.
设上半年每月平均用电量为x kW·h,
则下半年每月平均用电量为(x-2 000) kW·h.
上半年共用电6x kW·h,
下半年共用电6(x-2 000) kW·h.
根据全年用电15万kW·h,列得方程
6x+6(x -2 000)=150 000.
如果去括号,就能简化方程的形式.
下面的框图表示了解这个方程的流程.
去括号
6x + 6 ( x-2 000 ) = 150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
移项
合并同类项
系数化为1
由上可知,这个工厂去年上半年每月平均用电13500kW·h.
本题还有其他列方程的方法吗?
方程中等号左右两边都是一年中每两个月的平均用电量.
解法2:设上半年平均每月用电 x kW·h,根据题意可列方程
x+x-2000= .
移项,得 x+x= +2000
合并同类项,得 2x= 27000
系数化为1,得 x= 13500
答:这个工厂去年上半年每月平均用电13500kW·h.
例1 解下列方程:
(1) 2x - (x + 10) = 5x + 2(x - 1);
解:去括号,得 2x - x - 10 = 5x + 2x - 2.
移项,得 2x - x - 5x - 2x = -2 + 10.
合并同类项,得 -6x = 8.
系数化为 1,得 .
例1 解下列方程:
(2) 3x - 7(x - 1) = 3 - 2(x + 3);
解:去括号,得 3x - 7x + 7 = 3 - 2x - 6.
移项,得 3x - 7x + 2x = 3 - 6 - 7.
合并同类项,得 -2x = -10.
系数化为 1,得 x = 5.
归纳
解一元一次方程的一般步骤:
(1) 去括号;
(2) 移项;
(3) 合并同类项;
(4) 系数化为 1.
例2 一艘船从甲码头到乙码头顺流而行,用了 2 h;从乙码头返回甲码头逆流而行,用了 2.5 h.已知水流的速度是 3 km/h,求船在静水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间.
×
=
×
解:设船在静水中的平均速度为 x km/h,
则顺流速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得 2x + 6 = 2.5x-7.5.
移项、合并同类项,得 0.5x = 13.5.
系数化为1,得 x = 27.
答:船在静水中的平均速度为 27 km/h.
根据往返路程相等, 列得 2( x+3 ) = 2.5( x-3 ).
1. 解下列方程:
(1) 2(x + 3) = 5x;
解:去括号,得 2x + 6 = 5x.
移项,得 2x - 5x = -6.
合并同类项,得 -3x = -6.
系数化为 1,得 x = 2.
随堂练习
1. 解下列方程:
(2) 4x + 3(2x - 3) = 12 - (x + 4);
解:去括号,得 4x + 6x - 9= 12 – x - 4.
移项,得 4x + 6x + x= 12 – 4 + 9.
合并同类项,得 11x = 17.
系数化为 1,得 x =
1. 解下列方程:
(3) 2 – 3(x + 1) = 1 – 2(1 + 0.5x);
解:去括号,得 2 – 3x – 3 = 1 – 2 – x.
移项, 得 -3x+x = 1 – 2 – 2 + 3.
合并同类项,得 -2x = 0.
系数化为 1,得 x = 0.
2. 一架飞机在两城之间航行,风速为 24 km/h,顺风飞行要 2 小时 50 分,逆风飞行要 3 小时,求两城距离.
解:设飞机在无风时的速度为 x km/h,则在顺风中的速度为 (x+24) km/h ,在逆风中的速度为 (x-24)km/h.根据题意,得
(x+24)=3 (x-24)
去括号,得 x + 68 = 3x-72.
移项, 得 x - 3x = -72-68.
两城市的距离为 3×(840 - 24) = 2448 (km).
答:两城市之间的距离为 2448 km.
合并同类项,得 x = -140.
系数化为 1,得 x = 840.
课堂小结
解一元一次方程的一般步骤:
(1) 去括号;
(2) 移项;
(3) 合并同类项;
(4) 系数化为 1.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
