小学数学人教版四年级下《三角形的内角和》教学设计
文档属性
| 名称 | 小学数学人教版四年级下《三角形的内角和》教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 21:11:51 | ||
图片预览



文档简介
三角形的内角和
教学目标:
1.通过量、剪、拼等方法,探索和发现三角形内角和是180°。
2.在操作活动中,培养学生的合作能力、动手实践能力,发展学生的空间观念。并运用新知识解决问题。
3.使学生有科学实验态度,激发学生主动学习数学的兴趣,体验数学学习成功的喜悦。
教学重点:引导学生发现三角形内角和是180°
教学难点:用不同方法验证三角形的内角和是180°
教具学具准备:课件、学生准备不同类型的三角形各一个,量角器。
教学过程:
一、创设情景,引出问题
1.师:同学们,上节课我们共同学习了三角形的分类,现在老师想考考同学们对所学知识的掌握情况。
师出示课件,根据三角形内角的大小,把下面的三角形分类
在同学们的争论声中,教师教师揭示答案(根据三角形三个内角的大小,三角形可以分锐角三角形、直角三角形、钝角三角形。
2.师:为了内角的大小,三角形三兄弟争吵不休。教师出示课件
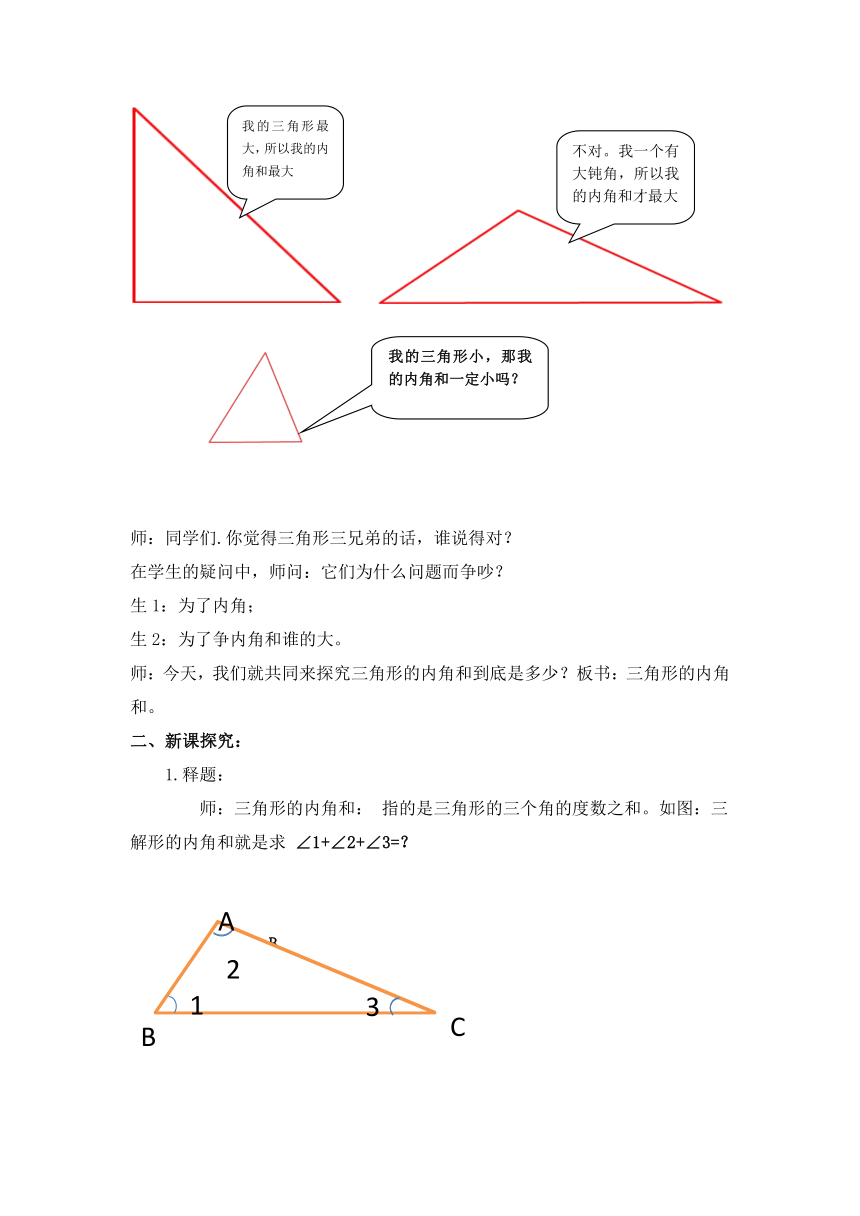
师:同学们.你觉得三角形三兄弟的话,谁说得对?
在学生的疑问中,师问:它们为什么问题而争吵?
生1:为了内角;
生2:为了争内角和谁的大。
师:今天,我们就共同来探究三角形的内角和到底是多少?板书:三角形的内角和。
二、新课探究:
1.释题:
师:三角形的内角和: 指的是三角形的三个角的度数之和。如图:三解形的内角和就是求 ∠1+∠2+∠3=?
B
2.探究三角形内角和
(1)师:同学们猜一猜,三角形三兄弟到底谁说的对呢,在同学们争执声中,师:大家意见不统一,我们得想个办法验证三角形的内角和是多少?可以用什么方法验证呢?
生:测量的方法。
师:你能说的更明白一些吗?
生:用量角器量每个角的大小,然后把量得度数加起来,就知道了三角形的内角和是多少了。如果学生不能回答用测量的方法来求三角形的内角和,师可以加以引导学生往测量方法上去求证。(如:要求∠1+∠2+∠3=?必须知道什么?用什么方法知道?从而引出有量角器量角的方法。)
(2)量一量
①小组合作探究
师:1.拿出自己准备好的三角形;
2. 用量角器量出每个内角的度数,用记号笔在角上标度数;
3.有困难的同学可寻求同桌帮助;
4.提前完成的同学举手示意,并坐好静听别人的发言。
5.音乐响开始,音乐停结束。
师在播放的轻音乐中,巡视学生测量的情况,并对困难的学生给予指导。
②汇报交流
师:(大部分的同学已经量好了。没有量好的同学,先停下来。让我们一起来分享其他同学的测量成果。出示已量好同学的作品,并让学生给大家汇报。请你给大家介绍你测量的三角形的形状,每个角的度数和内角和是多少?)学生汇报的时候教师板书。
学生的汇报中可能会出现答案不是惟一的情况。
(教师板书不同的情况,如:180°179°181°等)
分别对这几个数进行统计,度量结果是181度的同学请举手,179度的请举手,还有不一样的吗?
179°:有3人;180°:有40人,181的有2人等等。
师:观察这些测量结果你能发现什么?
生:都在180°左右。
(3)剪拼(撕拼)、折拼
①剪拼(撕拼)
预设1 :
师:用测量的方法验证,得到的结果不统一,有没有比测量更精确的验证方法?(让学生多思考),也就是不用度量你能用别的方法验证吗?
预设2:
师:不着急,看黑板(板书),内角和就是……? 生:就是把内角合并在一起。
师:度量的验证方法是分别量出每个角的度数,分成单个研究。如果把三个角合在一起考虑呢?你还有什么验证方法?
求三角形内角和就是把三角形的三个角和起来考虑问题,三个角和起来是什么角?三个角和起来是多少度的角,你有办法吗?
预设3:
师:如果三角形的内角和是180度,180度的角就是我们以前学过的平角
把三角形的三个角拼起来是不是一个平角?有什么方法能把三角形的三个内角合并在一起?
预设4:
师:我在电脑里收索一个验证方法。(课件演示)
生:把三角形的三个角剪下来,再拼成一个角。
师:你能说的更明白一些吗?
让学生在实物投影上演示(可以把剪下来的三个角,用固体胶固定在白色的长方形卡纸上。)
师:你们觉得他得方法可行吗?
师课件演示撕拼的方法,并让学生上台自己动手操作撕拼的方法加以验证。
②折拼
师:用剪拼的方法是比较精确,美中不足就是把三角形给剪了或是撕了,有没有更好验证方法?
在学生的疑问中师课件演示折拼的方法。
预设1师:要把三角形的三个角折成一个平角靠我们现在的经验是有点难。看电脑是怎样折的。
师:先要找到两条边的中点,用线连接起来,再按这条线折起来。再把另外的两个角折起来就可以了。(课件演示)
预设2学生不会想到用折的方法。
师:我在电脑里收索到折的方法,请同学们看一看他是怎么折的(课件演示
小结
师:这节课通过我们共同合作,我们用了几种方法来求证三角形的内角和
生:三种。
师:对,通过三种方法,我们知道了三角形的内角和是180°那为什么度量的方法会得到不同的结果?
学生可能问答不出来,这时师可以总结:可能是度量的时候有误差,如果准确
量结果就是180°(把不是180°的数据擦掉)
师:再出示三角形三兄弟争论的情景图,再一次询问谁说的对。这时学生会得出正确的答案。
师小结:三角形的内角和与三角形的形状和大小无关,都是180°板书,任何三角形的内角和和都是180°
三、巩固新知
1.下列说法,正确的划“√ ”,错误的划“×”
(1)小强量一个三角形的三个内角的度数分别是:80°、75° 、24°。( )
(2)用放大镜把一个三角形放大5倍后,它的内角 和就扩大了5倍。( )
(3)两个小三角形拼成一个大三角形,大三角形的内角和是360°。 ( )
2.在三角形中,∠1=140°∠3=25°,求∠2的度数。
刚才是已知两个内角的度数,求另一个内角的度数。如果只告诉你一个内角的度数,你会求出另外两个内角的度数吗?如果一个内角的度数也不告诉你,你能知道三个内角的度数吗?
4.请说出下列每个三角形每个角的度数。
180°÷3=60° 180°-96°=84° 180°-90°-40°=50°
84°÷2=42° 90°-40°=50°
四、课堂总结:
师:本节课学习,你有什么收获?
生:知道三角形的内角和与三角形的大小,形状无关,都是 180°
师,通过对本节课的学习,我们知道了三角形的内角和都是180°为了更容易的记住三角形的内角和,老师送给同学们四句口诀。课件展示:
三角形内角和口诀歌
三角形真奇怪, 有胖有瘦有高矮。
内角和都是180 ,我们时刻牢记它。
五、板书设计
三角形内角和
∠1+∠2+∠3=180°
三角形内角和三角形大小和形状无关
任何三角形的内角和都是180°
六、教学反思:
1.在让学生在动手撕一撕、拼一拼的环节中,因为时间的关系,没有让学生更多的去动手操作,教师只做了一个展示,只让一个学生进行了动操作展示,学生只通过看,而没有实际操作,故印象可能没动手操作的印象深。
2.在巩固新知第1题的判断题第(3)小题“把两个小三角形拼成一个大三角形,大三角形的内角和是360°。( )没有让学生动手摆一摆,去探索答案的正确与否,而是由教师讲解代替了学生探究的过程,学生只是机械记住了答案,有小部分学生可能不明白其中的道理地。
3.测量三角形三个内角等于180°的环节中,有两个学生测量得到184°和186°,如果在学生体验撕拼的方法后,让学生去撕一撕拼一拼这两个三角形,就能更好的验证学生测量时出现的错误,从而证明不管是任何形状的三角形都等于180°的结果。从而更能加深学生的印象。
4.在教学环节过渡中,还需注重一些细节的处理。
5.还应注生教学语言的规范化。
不对。我一个有大钝角,所以我的内角和才最大
我的三角形最大,所以我的内角和最大
我的三角形小,那我的内角和一定小吗?
2
C
1
A
B
3
140°
25°
180°-140°-25°=15°
180°-(140°+25°)=15°
3.一个直角三角形的一个锐角是35度,另一个锐角是多少度
35°
180°-90°-35°=55°
90°-35°=55°
?
2
C
1
A
B
3
教学目标:
1.通过量、剪、拼等方法,探索和发现三角形内角和是180°。
2.在操作活动中,培养学生的合作能力、动手实践能力,发展学生的空间观念。并运用新知识解决问题。
3.使学生有科学实验态度,激发学生主动学习数学的兴趣,体验数学学习成功的喜悦。
教学重点:引导学生发现三角形内角和是180°
教学难点:用不同方法验证三角形的内角和是180°
教具学具准备:课件、学生准备不同类型的三角形各一个,量角器。
教学过程:
一、创设情景,引出问题
1.师:同学们,上节课我们共同学习了三角形的分类,现在老师想考考同学们对所学知识的掌握情况。
师出示课件,根据三角形内角的大小,把下面的三角形分类
在同学们的争论声中,教师教师揭示答案(根据三角形三个内角的大小,三角形可以分锐角三角形、直角三角形、钝角三角形。
2.师:为了内角的大小,三角形三兄弟争吵不休。教师出示课件
师:同学们.你觉得三角形三兄弟的话,谁说得对?
在学生的疑问中,师问:它们为什么问题而争吵?
生1:为了内角;
生2:为了争内角和谁的大。
师:今天,我们就共同来探究三角形的内角和到底是多少?板书:三角形的内角和。
二、新课探究:
1.释题:
师:三角形的内角和: 指的是三角形的三个角的度数之和。如图:三解形的内角和就是求 ∠1+∠2+∠3=?
B
2.探究三角形内角和
(1)师:同学们猜一猜,三角形三兄弟到底谁说的对呢,在同学们争执声中,师:大家意见不统一,我们得想个办法验证三角形的内角和是多少?可以用什么方法验证呢?
生:测量的方法。
师:你能说的更明白一些吗?
生:用量角器量每个角的大小,然后把量得度数加起来,就知道了三角形的内角和是多少了。如果学生不能回答用测量的方法来求三角形的内角和,师可以加以引导学生往测量方法上去求证。(如:要求∠1+∠2+∠3=?必须知道什么?用什么方法知道?从而引出有量角器量角的方法。)
(2)量一量
①小组合作探究
师:1.拿出自己准备好的三角形;
2. 用量角器量出每个内角的度数,用记号笔在角上标度数;
3.有困难的同学可寻求同桌帮助;
4.提前完成的同学举手示意,并坐好静听别人的发言。
5.音乐响开始,音乐停结束。
师在播放的轻音乐中,巡视学生测量的情况,并对困难的学生给予指导。
②汇报交流
师:(大部分的同学已经量好了。没有量好的同学,先停下来。让我们一起来分享其他同学的测量成果。出示已量好同学的作品,并让学生给大家汇报。请你给大家介绍你测量的三角形的形状,每个角的度数和内角和是多少?)学生汇报的时候教师板书。
学生的汇报中可能会出现答案不是惟一的情况。
(教师板书不同的情况,如:180°179°181°等)
分别对这几个数进行统计,度量结果是181度的同学请举手,179度的请举手,还有不一样的吗?
179°:有3人;180°:有40人,181的有2人等等。
师:观察这些测量结果你能发现什么?
生:都在180°左右。
(3)剪拼(撕拼)、折拼
①剪拼(撕拼)
预设1 :
师:用测量的方法验证,得到的结果不统一,有没有比测量更精确的验证方法?(让学生多思考),也就是不用度量你能用别的方法验证吗?
预设2:
师:不着急,看黑板(板书),内角和就是……? 生:就是把内角合并在一起。
师:度量的验证方法是分别量出每个角的度数,分成单个研究。如果把三个角合在一起考虑呢?你还有什么验证方法?
求三角形内角和就是把三角形的三个角和起来考虑问题,三个角和起来是什么角?三个角和起来是多少度的角,你有办法吗?
预设3:
师:如果三角形的内角和是180度,180度的角就是我们以前学过的平角
把三角形的三个角拼起来是不是一个平角?有什么方法能把三角形的三个内角合并在一起?
预设4:
师:我在电脑里收索一个验证方法。(课件演示)
生:把三角形的三个角剪下来,再拼成一个角。
师:你能说的更明白一些吗?
让学生在实物投影上演示(可以把剪下来的三个角,用固体胶固定在白色的长方形卡纸上。)
师:你们觉得他得方法可行吗?
师课件演示撕拼的方法,并让学生上台自己动手操作撕拼的方法加以验证。
②折拼
师:用剪拼的方法是比较精确,美中不足就是把三角形给剪了或是撕了,有没有更好验证方法?
在学生的疑问中师课件演示折拼的方法。
预设1师:要把三角形的三个角折成一个平角靠我们现在的经验是有点难。看电脑是怎样折的。
师:先要找到两条边的中点,用线连接起来,再按这条线折起来。再把另外的两个角折起来就可以了。(课件演示)
预设2学生不会想到用折的方法。
师:我在电脑里收索到折的方法,请同学们看一看他是怎么折的(课件演示
小结
师:这节课通过我们共同合作,我们用了几种方法来求证三角形的内角和
生:三种。
师:对,通过三种方法,我们知道了三角形的内角和是180°那为什么度量的方法会得到不同的结果?
学生可能问答不出来,这时师可以总结:可能是度量的时候有误差,如果准确
量结果就是180°(把不是180°的数据擦掉)
师:再出示三角形三兄弟争论的情景图,再一次询问谁说的对。这时学生会得出正确的答案。
师小结:三角形的内角和与三角形的形状和大小无关,都是180°板书,任何三角形的内角和和都是180°
三、巩固新知
1.下列说法,正确的划“√ ”,错误的划“×”
(1)小强量一个三角形的三个内角的度数分别是:80°、75° 、24°。( )
(2)用放大镜把一个三角形放大5倍后,它的内角 和就扩大了5倍。( )
(3)两个小三角形拼成一个大三角形,大三角形的内角和是360°。 ( )
2.在三角形中,∠1=140°∠3=25°,求∠2的度数。
刚才是已知两个内角的度数,求另一个内角的度数。如果只告诉你一个内角的度数,你会求出另外两个内角的度数吗?如果一个内角的度数也不告诉你,你能知道三个内角的度数吗?
4.请说出下列每个三角形每个角的度数。
180°÷3=60° 180°-96°=84° 180°-90°-40°=50°
84°÷2=42° 90°-40°=50°
四、课堂总结:
师:本节课学习,你有什么收获?
生:知道三角形的内角和与三角形的大小,形状无关,都是 180°
师,通过对本节课的学习,我们知道了三角形的内角和都是180°为了更容易的记住三角形的内角和,老师送给同学们四句口诀。课件展示:
三角形内角和口诀歌
三角形真奇怪, 有胖有瘦有高矮。
内角和都是180 ,我们时刻牢记它。
五、板书设计
三角形内角和
∠1+∠2+∠3=180°
三角形内角和三角形大小和形状无关
任何三角形的内角和都是180°
六、教学反思:
1.在让学生在动手撕一撕、拼一拼的环节中,因为时间的关系,没有让学生更多的去动手操作,教师只做了一个展示,只让一个学生进行了动操作展示,学生只通过看,而没有实际操作,故印象可能没动手操作的印象深。
2.在巩固新知第1题的判断题第(3)小题“把两个小三角形拼成一个大三角形,大三角形的内角和是360°。( )没有让学生动手摆一摆,去探索答案的正确与否,而是由教师讲解代替了学生探究的过程,学生只是机械记住了答案,有小部分学生可能不明白其中的道理地。
3.测量三角形三个内角等于180°的环节中,有两个学生测量得到184°和186°,如果在学生体验撕拼的方法后,让学生去撕一撕拼一拼这两个三角形,就能更好的验证学生测量时出现的错误,从而证明不管是任何形状的三角形都等于180°的结果。从而更能加深学生的印象。
4.在教学环节过渡中,还需注重一些细节的处理。
5.还应注生教学语言的规范化。
不对。我一个有大钝角,所以我的内角和才最大
我的三角形最大,所以我的内角和最大
我的三角形小,那我的内角和一定小吗?
2
C
1
A
B
3
140°
25°
180°-140°-25°=15°
180°-(140°+25°)=15°
3.一个直角三角形的一个锐角是35度,另一个锐角是多少度
35°
180°-90°-35°=55°
90°-35°=55°
?
2
C
1
A
B
3
