人教版数学8年级上册 12.2 三角形全等的判定学案(含答案)
文档属性
| 名称 | 人教版数学8年级上册 12.2 三角形全等的判定学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览


文档简介
三角形全等的判定(3)
班级: 组号: 姓名:
一、旧知回顾
1.动手操作
(1)先任意画一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即使两角和它们的夹边对应相等)。
(2)把画好的△A′B′C′和△ABC比较一下,它们全等吗?
二、新知梳理
2.通过前面的动手操作,我们发现画好的△A′B′C′和△ABC全等,因此,我们得到全等三角形的判定定理3:_________________________________________________________。
(可以简写成_________________________)。
符号语言
3.思考课本P40的例4:①∠A=∠D,∠B=∠E,那么∠C=∠F吗?为什么?
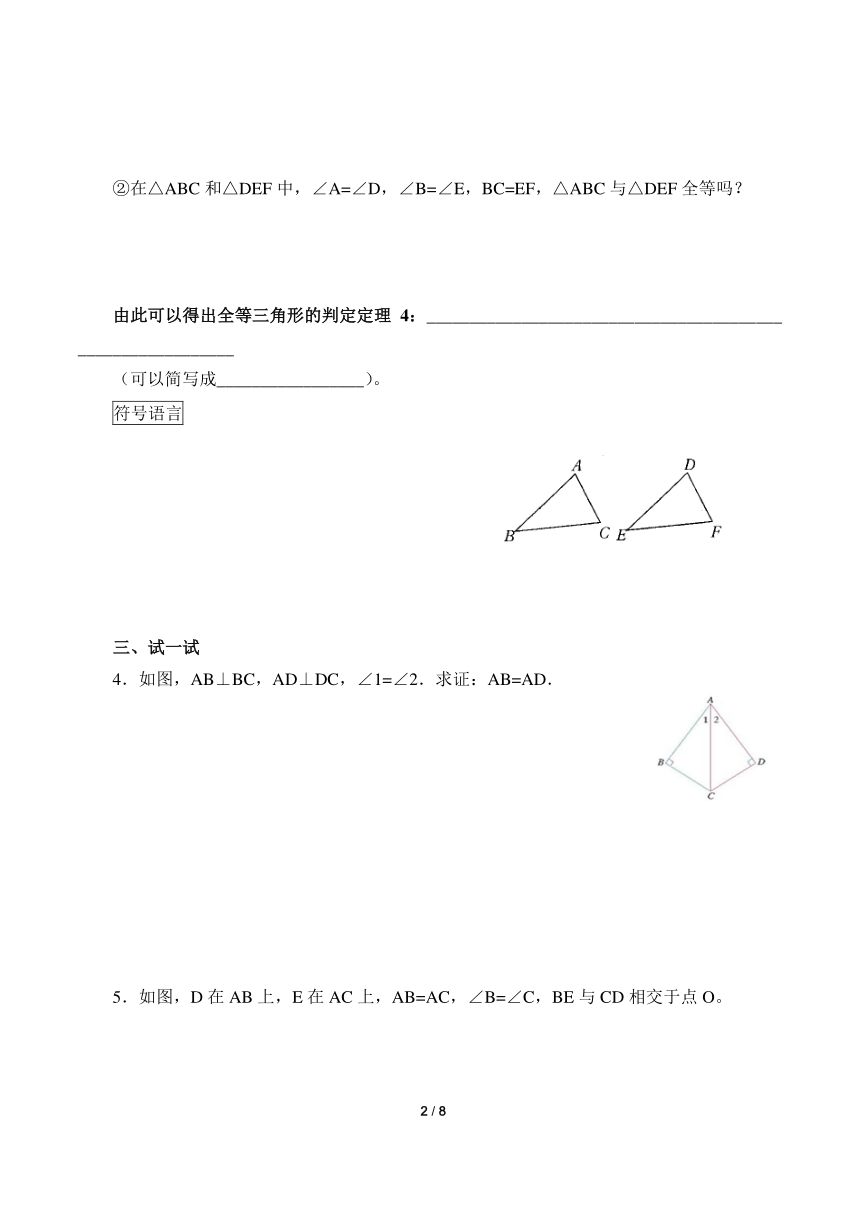
②在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?
由此可以得出全等三角形的判定定理4:___________________________________________________________
(可以简写成_________________)。
符号语言
三、试一试
4.如图,AB⊥BC,AD⊥DC,∠1=∠2.求证:AB=AD.
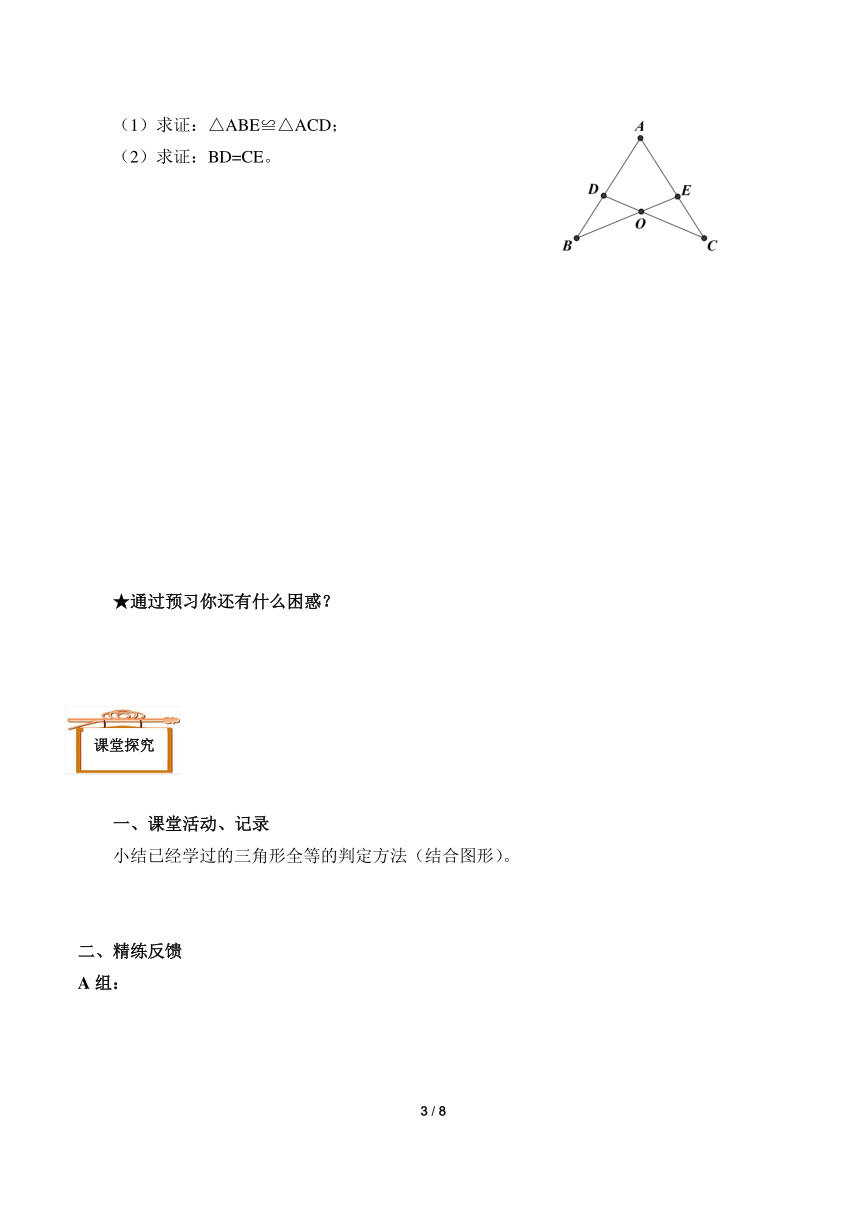
5.如图,D在AB上,E在AC上,AB=AC,∠B=∠C,BE与CD相交于点O。
(1)求证:△ABE≌△ACD;
(2)求证:BD=CE。
★通过预习你还有什么困惑?
一、课堂活动、记录
小结已经学过的三角形全等的判定方法(结合图形)。
二、精练反馈
A组:
1.如图,,,求证:。
B组:
2.如图,△ABC中,CA=CB,AD⊥BC,BE⊥AC,AD与BE相交于点O。
(1)求证:AD=BE。
(2)图中共有______对全等三角形,它们分别是_______________________________。
(3)请你选出一对,加以证明。
三、课堂小结
1.证明两个三角形全等有几种方法?如何正确选择和应用这些方法?
2.全等三角形性质可以用来证明哪些问题?举例说明。
四、拓展延伸(选做题)
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E。AD⊥CE于点D.
求证:△BEC≌△CDA.
【答案】
【学前准备】
1.略
2.两角和它们的夹边对应相等的两个三角形全等 ASA
符号语言:
在△ABC和△中
∴△ABC≌△(ASA)
3.①相等 ∵∠A=∠D,∠B=∠E ∴∠A+∠B+∠C=180°∠D+∠E+∠F=90°
∴∠C=∠F
②全等
两角和其中一个角的对边对应相等的两个三角形全等 AAS
符号语言:
在△ABC和△DEF中
∴△ABC≌△DEF(AAS)
4.证明:∵AB⊥BC,AD⊥DC
∴∠B=∠D=90°
在△ABC和△ADC中
∴△ABC≌△ADC(AAS)
∴AB=AD
5.略
【课堂探究】
课堂活动、记录
略
精练反馈
1.证明:∵ ∴∠1+∠D=∠2+∠C ∴∠D=∠C
在△DAB和△CAB中
∴△DAB≌△CAB(AAS)
∴
2.(1)证明:∵AD⊥BC,BE⊥AC
∴∠CEB=∠CDA=90°
在△ADC和△BCE
∴△ADC≌△BCE(AAS) ∴AD=BE
(2)△AEB≌△ADB
(3)∵AD⊥BC,BE⊥AC
∴∠AEB=∠DAB=90
∵△ADC≌△BCE ∴CE=CD ∴AC-CE=BC-CD ∴AE=BD
在△AOE和△BOD中
∴△AOE≌△BOD(AAS)
课堂小结
略
拓展延伸
证明:
∵∠ACB=90°
∴°
∵BE⊥CE AD⊥CE
∴∠BEC=90° ∠ADC=90°
∴∠EBC+∠BCE=90°
∴∠ACD=∠CBE
∴在△BEC和△CDA中
∴△BEC≌△CDA(AAS)
8 / 8
班级: 组号: 姓名:
一、旧知回顾
1.动手操作
(1)先任意画一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即使两角和它们的夹边对应相等)。
(2)把画好的△A′B′C′和△ABC比较一下,它们全等吗?
二、新知梳理
2.通过前面的动手操作,我们发现画好的△A′B′C′和△ABC全等,因此,我们得到全等三角形的判定定理3:_________________________________________________________。
(可以简写成_________________________)。
符号语言
3.思考课本P40的例4:①∠A=∠D,∠B=∠E,那么∠C=∠F吗?为什么?
②在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?
由此可以得出全等三角形的判定定理4:___________________________________________________________
(可以简写成_________________)。
符号语言
三、试一试
4.如图,AB⊥BC,AD⊥DC,∠1=∠2.求证:AB=AD.
5.如图,D在AB上,E在AC上,AB=AC,∠B=∠C,BE与CD相交于点O。
(1)求证:△ABE≌△ACD;
(2)求证:BD=CE。
★通过预习你还有什么困惑?
一、课堂活动、记录
小结已经学过的三角形全等的判定方法(结合图形)。
二、精练反馈
A组:
1.如图,,,求证:。
B组:
2.如图,△ABC中,CA=CB,AD⊥BC,BE⊥AC,AD与BE相交于点O。
(1)求证:AD=BE。
(2)图中共有______对全等三角形,它们分别是_______________________________。
(3)请你选出一对,加以证明。
三、课堂小结
1.证明两个三角形全等有几种方法?如何正确选择和应用这些方法?
2.全等三角形性质可以用来证明哪些问题?举例说明。
四、拓展延伸(选做题)
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E。AD⊥CE于点D.
求证:△BEC≌△CDA.
【答案】
【学前准备】
1.略
2.两角和它们的夹边对应相等的两个三角形全等 ASA
符号语言:
在△ABC和△中
∴△ABC≌△(ASA)
3.①相等 ∵∠A=∠D,∠B=∠E ∴∠A+∠B+∠C=180°∠D+∠E+∠F=90°
∴∠C=∠F
②全等
两角和其中一个角的对边对应相等的两个三角形全等 AAS
符号语言:
在△ABC和△DEF中
∴△ABC≌△DEF(AAS)
4.证明:∵AB⊥BC,AD⊥DC
∴∠B=∠D=90°
在△ABC和△ADC中
∴△ABC≌△ADC(AAS)
∴AB=AD
5.略
【课堂探究】
课堂活动、记录
略
精练反馈
1.证明:∵ ∴∠1+∠D=∠2+∠C ∴∠D=∠C
在△DAB和△CAB中
∴△DAB≌△CAB(AAS)
∴
2.(1)证明:∵AD⊥BC,BE⊥AC
∴∠CEB=∠CDA=90°
在△ADC和△BCE
∴△ADC≌△BCE(AAS) ∴AD=BE
(2)△AEB≌△ADB
(3)∵AD⊥BC,BE⊥AC
∴∠AEB=∠DAB=90
∵△ADC≌△BCE ∴CE=CD ∴AC-CE=BC-CD ∴AE=BD
在△AOE和△BOD中
∴△AOE≌△BOD(AAS)
课堂小结
略
拓展延伸
证明:
∵∠ACB=90°
∴°
∵BE⊥CE AD⊥CE
∴∠BEC=90° ∠ADC=90°
∴∠EBC+∠BCE=90°
∴∠ACD=∠CBE
∴在△BEC和△CDA中
∴△BEC≌△CDA(AAS)
8 / 8
