冀教版数学八年级上册单元检测卷 第十六章 轴对称和中心对称(测基础)(含解析)
文档属性
| 名称 | 冀教版数学八年级上册单元检测卷 第十六章 轴对称和中心对称(测基础)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 22:41:09 | ||
图片预览



文档简介
轴对称和中心对称
(测基础)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.已知,,用尺规作图的方法在上确定一点P,使,则符合要求的作图痕迹是( )
A. B.
C. D.
3.在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边上高的交点 D.三边中垂线的交点
4.如图,已知在中,CD是AB边上的高线,BE平分交CD于点E,,,则的面积等于( )
A.10 B.7 C.5 D.4
5.如图,与关于直线MN轴对称,则下列结论中错误的是( )
A. B.
C. D.AD的连线被MN垂直平分
6.如图,现要在三角形的草坪,上建一个凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高线的交点
D.三边中垂线的交点
7.如图,在的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且阴影部分组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
8.如图,在四边形中,,,面积为21,的垂直平分线分别交,于点M,N,若点P和点Q分别是线段和边上的动点,则的最小值为( )
A.5 B.6 C.7 D.8
9.如图,OP平分,,,垂足分别为A,B.下列结论中不一定成立的是( )
A. B.PO平分 C. D.AB垂直平分OP
10.如图,,M是的中点,平分,且,则( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.如图,不考虑阴影,图形的对称轴是直线l,其中圆的面积为4π,则阴影部分的面积是____________.
12.如图,如果与关于点O成中心对称,那么:
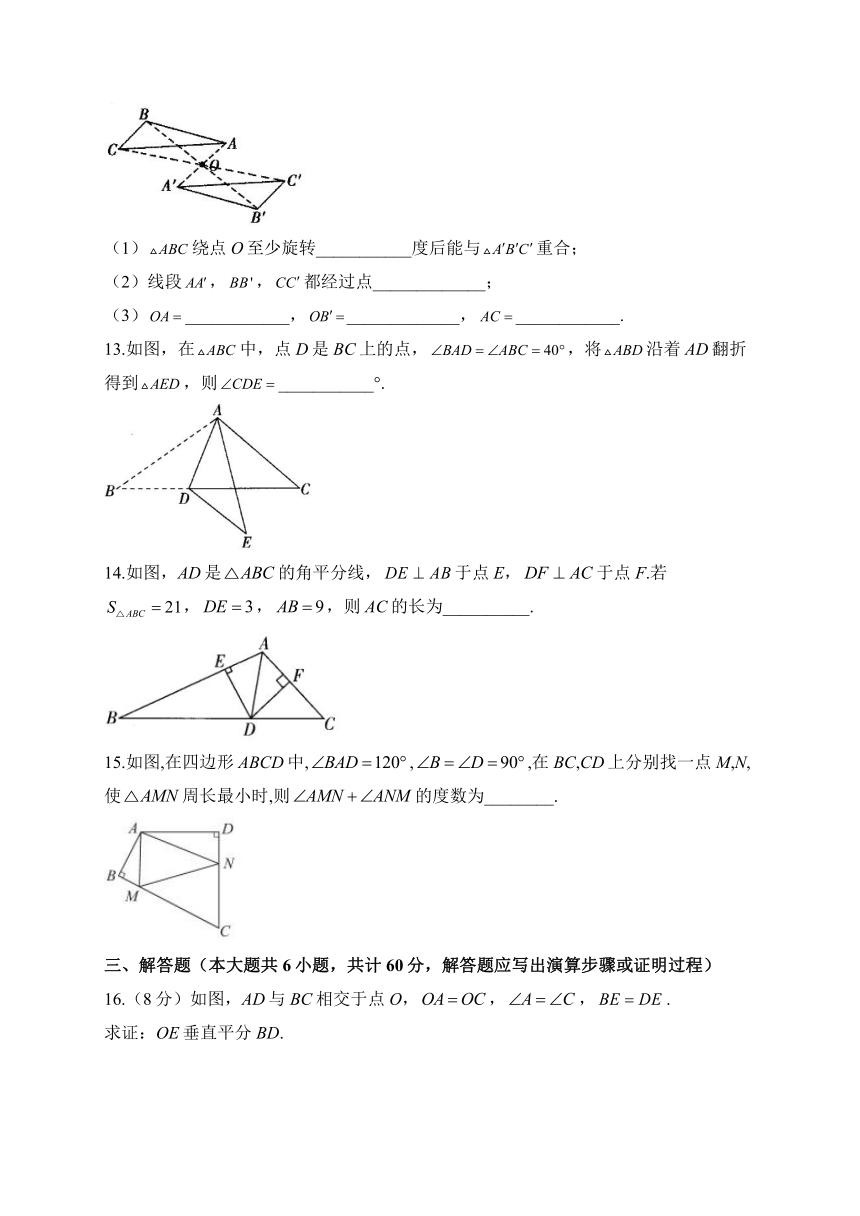
(1)绕点O至少旋转___________度后能与重合;
(2)线段,,都经过点_____________;
(3)____________,_____________,____________.
13.如图,在中,点D是BC上的点,,将沿着AD翻折得到,则___________°.
14.如图,AD是的角平分线,于点E,于点F.若,,,则AC的长为__________.
15.如图,在四边形ABCD中,,,在BC,CD上分别找一点M,N,使周长最小时,则的度数为________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,AD与BC相交于点O,,,.
求证:OE垂直平分BD.
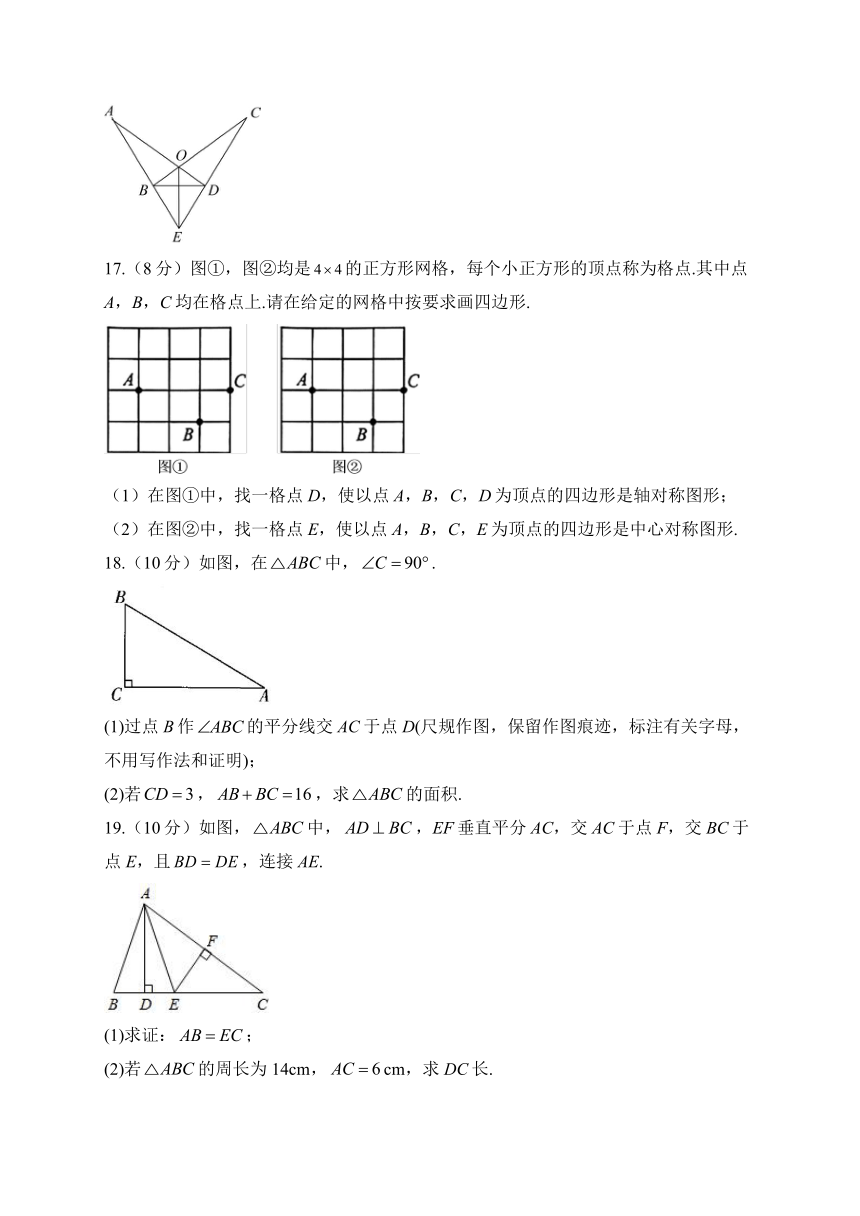
17.(8分)图①,图②均是的正方形网格,每个小正方形的顶点称为格点.其中点A,B,C均在格点上.请在给定的网格中按要求画四边形.
(1)在图①中,找一格点D,使以点A,B,C,D为顶点的四边形是轴对称图形;
(2)在图②中,找一格点E,使以点A,B,C,E为顶点的四边形是中心对称图形.
18.(10分)如图,在中,.
(1)过点B作的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
19.(10分)如图,中,,EF垂直平分AC,交AC于点F,交BC于点E,且,连接AE.
(1)求证:;
(2)若的周长为14cm,cm,求DC长.
20.(12分)如图1,网格中的每一个正方形的边长为1,为格点三角形(点A、B、C在小正方形的顶点上),直线m为格点直线(直线m经过小正方形的格点).
(1)如图1,作出关于直线m的轴对称图形;
(2)如图2,在直线m上找到一点P,使的值最小;
(3)如图3,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
(4)如图4,仅用直尺作出三角形ABC的边AB上的高,简单说明你的理由.
21.(12分)如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
答案以及解析
1.答案:D
解析:A.原图是轴对称图形,不是中心对称图形,故本选项不合题意;
B.原图是轴对称图形,不是中心对称图形,故本选项不合题意;
C.原图是中心对称图形,不是轴对称图形,故本选项不合题意;
D.原图既是中心对称图形,又是轴对称图形,故本选项符合题意.
故选:D.
2.答案:D
解析:由D中作图可知,点P是边的垂直平分线上的点,则,
所以.
故选:D.
3.答案:D
解析:利用线段垂直平分线的性质得:要放在三边中垂线的交点上.
故选:D.
4.答案:C
解析:作于F,
平分,,,
,.
故选:C.
5.答案:A
解析:与关于直线MN轴对称,
,,AD的连线被MN垂直平分,
B,C,D正确,
故选:A.
6.答案:A
7.答案:C
解析:如图,共有4种作法.
8.答案:C
解析:连接AQ,过点D作,
,面积为21,
,
,
MN垂直平分AB,
,
,
当AQ的值最小时,的值最小,根据垂线段最短可知,当时,AQ的值最小,
,
,
的值最小值为7;
故选C.
9.答案:D
解析:因为OP平分,,,所以,,,所以,所以,,所以A,B,C中的结论一定成立,故选D.
10.答案:B
解析:如图,过点M作于点N.
,.平分,,.是的中点,.又,平分,.故选B.
11.答案:2π
解析:由轴对称的性质可得,图中阴影部分的面积正好等于圆面积的一半,所以阴影部分的面积.
12.答案:(1)180;(2)O;(3),OB,
解析:(1)因为与关于点O成中心对称,所以绕点O至少旋转180°后能与重合;
(2)由中心对称的性质,得对称点的连线,,都经过对称中心点O;
(3)因为对称点的连线被对称中心平分,成中心对称的两个图形全等,所以,,.
13.答案:20
解析:,将沿着AD翻折得到,,,.
14.答案:5
解析:是的角平分线,,,.,,即,.
15.答案:
解析:作A关于BC和CD的对称点,,连接,交BC于M,交CD于N,则即为的周长最小值.作DA延长线AH,
,
,,
,,,,
故答案为:.
16.解析:在与中,
,,,
,
,
点O在线段BD的垂直平分线上,
,
点E在线段BD的垂直平分线上,
OE垂直平分BD.
17.解析:(1)点D如图(1)所示,此时四边形ABCD是轴对称图形.
(2)点E如图(2)所示,此时四边形ABCE是中心对称图形.
18.解析:(1)的平分线如图中BD所示.
(2)如图,过点D作于H.
平分,,,
,
的面积
.
19.答案:(1)证明见解析
(2)
解析:(1)证明:EF垂直平分AC,
,
,,
,
;
(2)解:的周长为14cm,
(cm),
cm,
(cm),
,,
(cm).
20.答案:解析:(1)如图所示,即为所求作,
(2)如图,点P即为所求作,
(3)如图,即为所作,
(4)如图,选择格点D、E,
证明,于是,,
选择格点Q,证明,于是,,
为线段AB的垂直平分线,设CQ与AB相交于点F,则CF为所要求的的边AB上的高.
21.答案:证明:(1),,
AM平分,DM平分,
,
,
,即.
(2)如图,过M作,垂足为点N,
,,
,,
AM平分,DM平分,
,,
,即M为BC的中点.
(测基础)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.已知,,用尺规作图的方法在上确定一点P,使,则符合要求的作图痕迹是( )
A. B.
C. D.
3.在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边上高的交点 D.三边中垂线的交点
4.如图,已知在中,CD是AB边上的高线,BE平分交CD于点E,,,则的面积等于( )
A.10 B.7 C.5 D.4
5.如图,与关于直线MN轴对称,则下列结论中错误的是( )
A. B.
C. D.AD的连线被MN垂直平分
6.如图,现要在三角形的草坪,上建一个凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高线的交点
D.三边中垂线的交点
7.如图,在的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且阴影部分组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
8.如图,在四边形中,,,面积为21,的垂直平分线分别交,于点M,N,若点P和点Q分别是线段和边上的动点,则的最小值为( )
A.5 B.6 C.7 D.8
9.如图,OP平分,,,垂足分别为A,B.下列结论中不一定成立的是( )
A. B.PO平分 C. D.AB垂直平分OP
10.如图,,M是的中点,平分,且,则( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.如图,不考虑阴影,图形的对称轴是直线l,其中圆的面积为4π,则阴影部分的面积是____________.
12.如图,如果与关于点O成中心对称,那么:
(1)绕点O至少旋转___________度后能与重合;
(2)线段,,都经过点_____________;
(3)____________,_____________,____________.
13.如图,在中,点D是BC上的点,,将沿着AD翻折得到,则___________°.
14.如图,AD是的角平分线,于点E,于点F.若,,,则AC的长为__________.
15.如图,在四边形ABCD中,,,在BC,CD上分别找一点M,N,使周长最小时,则的度数为________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,AD与BC相交于点O,,,.
求证:OE垂直平分BD.
17.(8分)图①,图②均是的正方形网格,每个小正方形的顶点称为格点.其中点A,B,C均在格点上.请在给定的网格中按要求画四边形.
(1)在图①中,找一格点D,使以点A,B,C,D为顶点的四边形是轴对称图形;
(2)在图②中,找一格点E,使以点A,B,C,E为顶点的四边形是中心对称图形.
18.(10分)如图,在中,.
(1)过点B作的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
19.(10分)如图,中,,EF垂直平分AC,交AC于点F,交BC于点E,且,连接AE.
(1)求证:;
(2)若的周长为14cm,cm,求DC长.
20.(12分)如图1,网格中的每一个正方形的边长为1,为格点三角形(点A、B、C在小正方形的顶点上),直线m为格点直线(直线m经过小正方形的格点).
(1)如图1,作出关于直线m的轴对称图形;
(2)如图2,在直线m上找到一点P,使的值最小;
(3)如图3,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
(4)如图4,仅用直尺作出三角形ABC的边AB上的高,简单说明你的理由.
21.(12分)如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
答案以及解析
1.答案:D
解析:A.原图是轴对称图形,不是中心对称图形,故本选项不合题意;
B.原图是轴对称图形,不是中心对称图形,故本选项不合题意;
C.原图是中心对称图形,不是轴对称图形,故本选项不合题意;
D.原图既是中心对称图形,又是轴对称图形,故本选项符合题意.
故选:D.
2.答案:D
解析:由D中作图可知,点P是边的垂直平分线上的点,则,
所以.
故选:D.
3.答案:D
解析:利用线段垂直平分线的性质得:要放在三边中垂线的交点上.
故选:D.
4.答案:C
解析:作于F,
平分,,,
,.
故选:C.
5.答案:A
解析:与关于直线MN轴对称,
,,AD的连线被MN垂直平分,
B,C,D正确,
故选:A.
6.答案:A
7.答案:C
解析:如图,共有4种作法.
8.答案:C
解析:连接AQ,过点D作,
,面积为21,
,
,
MN垂直平分AB,
,
,
当AQ的值最小时,的值最小,根据垂线段最短可知,当时,AQ的值最小,
,
,
的值最小值为7;
故选C.
9.答案:D
解析:因为OP平分,,,所以,,,所以,所以,,所以A,B,C中的结论一定成立,故选D.
10.答案:B
解析:如图,过点M作于点N.
,.平分,,.是的中点,.又,平分,.故选B.
11.答案:2π
解析:由轴对称的性质可得,图中阴影部分的面积正好等于圆面积的一半,所以阴影部分的面积.
12.答案:(1)180;(2)O;(3),OB,
解析:(1)因为与关于点O成中心对称,所以绕点O至少旋转180°后能与重合;
(2)由中心对称的性质,得对称点的连线,,都经过对称中心点O;
(3)因为对称点的连线被对称中心平分,成中心对称的两个图形全等,所以,,.
13.答案:20
解析:,将沿着AD翻折得到,,,.
14.答案:5
解析:是的角平分线,,,.,,即,.
15.答案:
解析:作A关于BC和CD的对称点,,连接,交BC于M,交CD于N,则即为的周长最小值.作DA延长线AH,
,
,,
,,,,
故答案为:.
16.解析:在与中,
,,,
,
,
点O在线段BD的垂直平分线上,
,
点E在线段BD的垂直平分线上,
OE垂直平分BD.
17.解析:(1)点D如图(1)所示,此时四边形ABCD是轴对称图形.
(2)点E如图(2)所示,此时四边形ABCE是中心对称图形.
18.解析:(1)的平分线如图中BD所示.
(2)如图,过点D作于H.
平分,,,
,
的面积
.
19.答案:(1)证明见解析
(2)
解析:(1)证明:EF垂直平分AC,
,
,,
,
;
(2)解:的周长为14cm,
(cm),
cm,
(cm),
,,
(cm).
20.答案:解析:(1)如图所示,即为所求作,
(2)如图,点P即为所求作,
(3)如图,即为所作,
(4)如图,选择格点D、E,
证明,于是,,
选择格点Q,证明,于是,,
为线段AB的垂直平分线,设CQ与AB相交于点F,则CF为所要求的的边AB上的高.
21.答案:证明:(1),,
AM平分,DM平分,
,
,
,即.
(2)如图,过M作,垂足为点N,
,,
,,
AM平分,DM平分,
,,
,即M为BC的中点.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
