冀教版数学八年级上册单元检测卷 第十六章 轴对称和中心对称(测能力)(含解析)
文档属性
| 名称 | 冀教版数学八年级上册单元检测卷 第十六章 轴对称和中心对称(测能力)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 22:42:01 | ||
图片预览



文档简介
轴对称和中心对称
(测能力)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
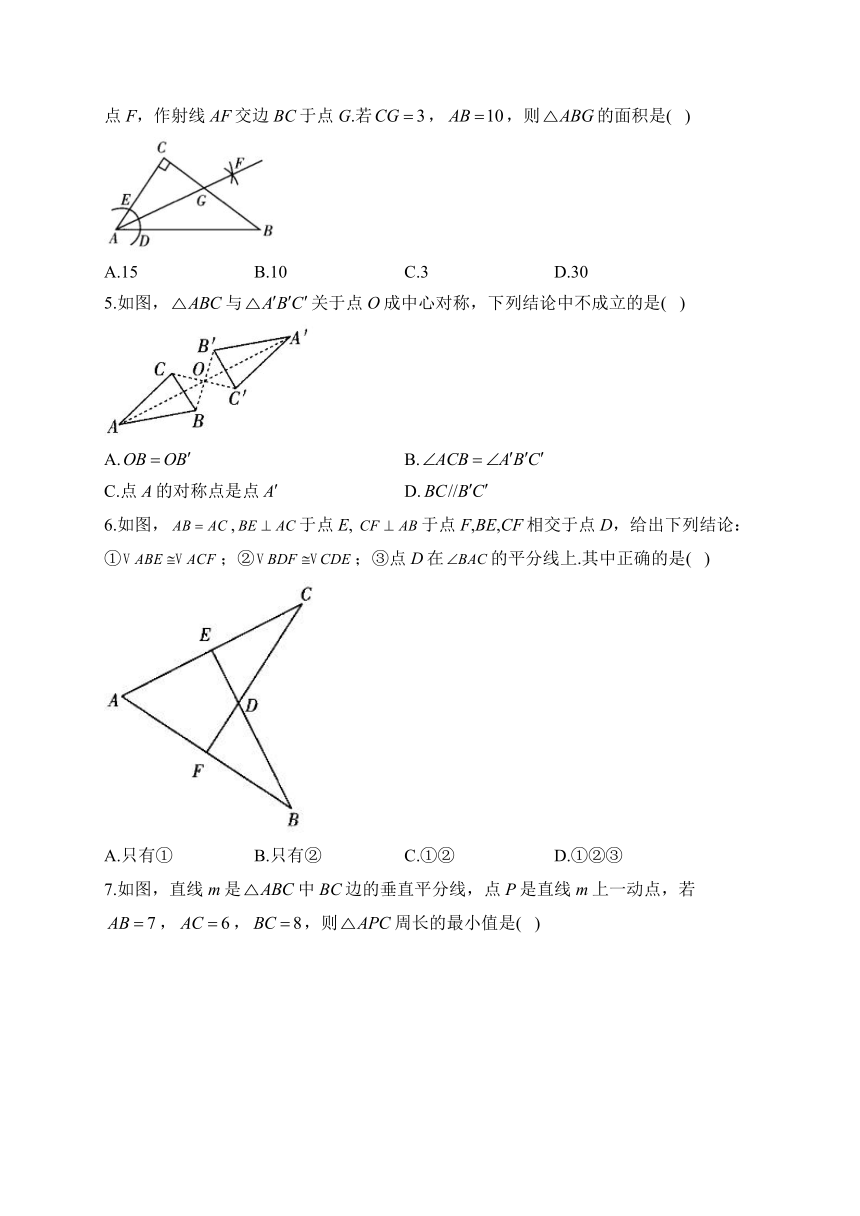
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,在中,.用直尺和圆规在边上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
3.如图,若与关于直线MN对称,交MN于点O,则下列说法中,不一定正确的是( )
A. B. C. D.
4.如图,在中,,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E,再分别以点D,E为圆心,大于的长为半径画弧,两弧交于点F,作射线AF交边BC于点G.若,,则的面积是( )
A.15 B.10 C.3 D.30
5.如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B.
C.点A的对称点是点 D.
6.如图,,于点E, 于点F,BE,CF相交于点D,给出下列结论:①;②;③点D在的平分线上.其中正确的是( )
A.只有① B.只有② C.①② D.①②③
7.如图,直线m是中BC边的垂直平分线,点P是直线m上一动点,若,,,则周长的最小值是( )
A.13 B.14 C.15 D.13.5
8.如图,的三边AB,BC,CA长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( )
A. B. C. D.
9.如图,中,AD是的角平分线,,F是BC中点,连接AF,若,,,则为( )
A.7.5 B.12 C.15 D.30
10.如图,在中,和的平分线AE、BF相交于点O,AE交BC于E,BF交AC于F,过点O作于D,下列四个结论:
①;②当时,;③若,,则.
其中正确的是( )
A.①② B.②③ C.①②③ D.①③
二、填空题(每小题4分,共20分)
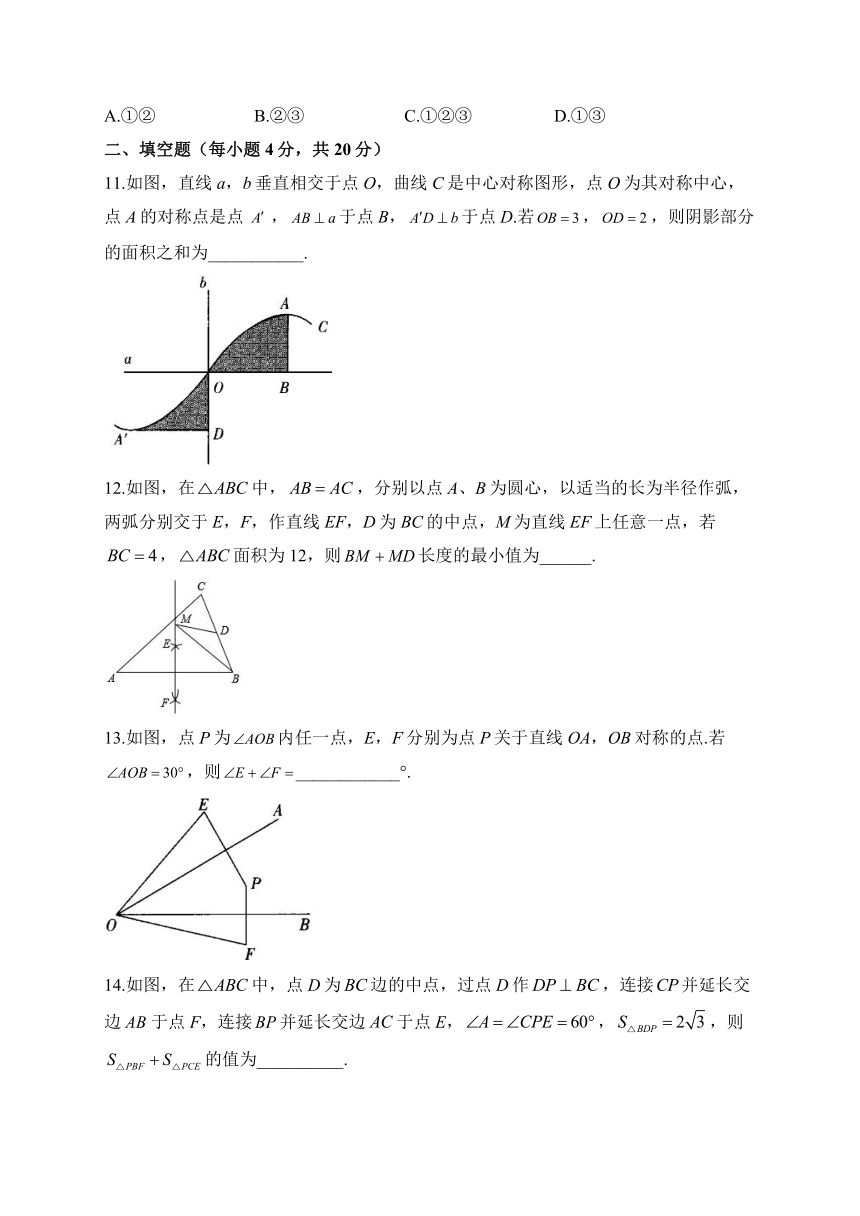
11.如图,直线a,b垂直相交于点O,曲线C是中心对称图形,点O为其对称中心,点A的对称点是点,于点B,于点D.若,,则阴影部分的面积之和为___________.
12.如图,在中,,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点,若,面积为12,则长度的最小值为______.
13.如图,点P为内任一点,E,F分别为点P关于直线OA,OB对称的点.若,则____________°.
14.如图,在中,点D为边的中点,过点D作,连接并延长交边于点F,连接并延长交边于点E,,,则的值为__________.
15.如图,四边形ABCD的对角线AC,BD相交于点O,.下列结论:
①;
②;
③;
④;
⑤四边形ABCD是轴对称图形.其中所有正确结论的序号是________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在四边形ABCD中,
(1)画出四边形,使四边形与四边形ABCD关于直线MN成轴对称;
(2)画出四边形,使四边形与四边形ABCD关于点O中心对称;
(3)四边形与四边形是否对称,若对称请在图中画出对称轴或对称中心.
17.(8分)如图,在中,,点M,N分别在边AB,BC上,连接AN,且和关于直线MN对称.
(1)若,则的度数为______.
(2)若,,且的周长为36,求的周长.
18.(10分)如图,,点M,N分别是边,上的定点,点P,Q分别是边、上的动点.
(1)画图说明,当最小时,找出P和Q的位置.
(2)记,,当最小时,求的值.
19.(10分)(1)如图①,O为AB的中点,直线、分别经过点O、B,且,以点O为圆心,OA长为半径画弧交直线于点C,连接AC.求证:直线垂直平分AC;
(2)如图②,平面内直线,且相邻两直线间距离相等,点P、Q分别在直线、上,连接PQ.用圆规和无刻度的直尺在直线上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)
20.(12分)教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,的周长是12,BO,CO分别平分和,于点D,若,则的面积为________.
21.(12分)如图,
(1)【情景呈现】画,并画的平分线OC.把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与的两边OA,OB相交于点E,F,若,(如图1),则;若把三角尺绕点P旋转(如图2),则_________.(选填“<”,“>”或“=”)(不用证明)
(2)【理解应用】在(1)的条件下,过点P作直线,分别交OA,OB于点G,H,如图3.
①图中全等三角形共有_________对;(不添加辅助线)
②直接写出与之间的数量关系为_________.
(3)【拓展延伸】如图4,画,并画的平分线OC,在OC上任取一点P,作,当时,的两边分别与OA,OB相交于点E,F,PE与PF相等吗?请说明理由.
答案以及解析
1.答案:D
解析:A、是轴对称图形,不是中心对称图形,故A选项不合题意;
B、是轴对称图形,不是中心对称图形,故B选项不符合题意;
C、不是轴对称图形,是中心对称图形,故C选项不合题意;
D、既是轴对称图形,又是中心对称图形,故D选项合题意.
故选:D.
2.答案:C
解析:点P到点A、点B的距离相等,
点P在线段的垂直平分线上,
故选:C.
3.答案:B
解析:与关于直线MN对称,,,,故选项A,C,D正确.
4.答案:A
解析:由题意得AG是的角平分线,如图,过点G作于点H.,,的面积.故选A.
5.答案:B
解析:与关于点O成中心对称,,,点A的对称点是点,,故A,C,D正确.
6.答案:D
解析:,又,①正确;,又,,②正确;,,又,点D在的平分线上,③正确.故选D.
7.答案:A
解析:直线m是中BC边的垂直平分线,
,
周长,
两点之间线段最短,
,
的周长,
,,
周长最小为,
故选:A.
8.答案:C
解析:过点O作于D,于E,于F,
点O是内心,
,
,
故选:C.
9.答案:A
解析:如图,过点D作于点G,
AD是的角平分线,,,
,
,
F是BC中点,
.
故选:A.
10.答案:B
解析:和的平分线AE、BF相交于点O,
,,
,故①错误;
,
,
,
,
,
如图,在AB上取一点H,使,
BF是的角平分线,
,
,
,
,
,
,
,,
,
,
,故②正确;
作于G,于M,如图所示:
和的平分线AE、BF相交于点O,
点O在的平分线上,
,
,故③正确;
故选:B.
11.答案:6
解析:过点A作于点E,曲线C是中心对称图形,点A的对称点是点,,,阴影部分的面积之和等于四边形ABOE的面积,,,,阴影部分的面积之和为.
12.答案:6
解析:如图,连接AD,AM,
因为,D为BC的中点,
所以
因为,
所以,
因为EF垂直平分线段AB,
所以,
所以,
所以的最小值为6,
故答案为:6.
13.答案:150
解析:如图,连接OP,E,F分别为点P关于直线OA,OB对称的点,,,,,,,又,,.
14.答案:
解析:作于点M,于点N,
点D为边的中点,,
,
,
,,且,
,
,,,
,
,
,
,
在和中,,
,
,,
,
,,
,
,且,,
,
,
,
故答案为:.
15.答案:①②③⑤
解析:,
,,,,
,故①正确;
四边形ABCD的对角线AC,BD相交于点O,
,
在和中,
,
,故③正确;
,故②正确.
,,
四边形ABCD是轴对称图形,故⑤正确.
故答案为:①②③⑤.
16.答案:(1)图见解析;
(2)图见解析;
(3)图见解析;
解析:(1)四边形如图所示;
(2)四边形如图所示;
(3)如图所示,四边形与四边形关于直线PQ成轴对称.
17.答案:(1)
(2)21
解析:(1),,
,
和关于直线MN对称,
,
,
故答案为:.
(2)的周长为36,
,
,,
,解得,
.
和关于直线MN对称,
,
的周长.
18.答案:(1)见解析
(2)
解析:(1)如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,如图所示:
(2)由(1)知M关于的对称点,N关于的对称点,
,,
,
,
.
19.答案:(1)解:如图①,连接OC,
,,
直线平分AC,
由作图可知:,
,
垂直AC,
,
垂直AC,
即直线垂直平分AC.
(2)如图②,以与PQ的交点O为圆心,OP长为半径画弧交直线于点C,连接PC并延长交直线于点D,此时线段PD最短,点D即为所求.
解析:
20.答案:定理证明:见解析,定理应用:18
解析:定理证明:是的角平分线,
,
,,
,
在和中,
,
,
;
定理应用:过O作与E,于F,
,CO分别平分和,
,,
,
,
的周长是12,
,
的面积:,
故答案为:18.
21.答案:(1)=
(2)①3②
(3),理由见解析
解析:(1)如图,过点P作,,垂足是M,N,
,
,
OC是的平分线,
,
,
,
,
在和中,
,
,
.
故答案为:=;
(2)①OC平分,
,
,
,
,
,
,
在和中,
,
,
同理可证明,
,
,
全等三角形有3对;
②,,
,
,,
.
故答案为:①3;②;
(3)如图,作于G,于H,
,,
,
OC平分,
,
,,且,
又,
,
,
,
在和中,
,
,
.
(测能力)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,在中,.用直尺和圆规在边上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
3.如图,若与关于直线MN对称,交MN于点O,则下列说法中,不一定正确的是( )
A. B. C. D.
4.如图,在中,,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E,再分别以点D,E为圆心,大于的长为半径画弧,两弧交于点F,作射线AF交边BC于点G.若,,则的面积是( )
A.15 B.10 C.3 D.30
5.如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B.
C.点A的对称点是点 D.
6.如图,,于点E, 于点F,BE,CF相交于点D,给出下列结论:①;②;③点D在的平分线上.其中正确的是( )
A.只有① B.只有② C.①② D.①②③
7.如图,直线m是中BC边的垂直平分线,点P是直线m上一动点,若,,,则周长的最小值是( )
A.13 B.14 C.15 D.13.5
8.如图,的三边AB,BC,CA长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( )
A. B. C. D.
9.如图,中,AD是的角平分线,,F是BC中点,连接AF,若,,,则为( )
A.7.5 B.12 C.15 D.30
10.如图,在中,和的平分线AE、BF相交于点O,AE交BC于E,BF交AC于F,过点O作于D,下列四个结论:
①;②当时,;③若,,则.
其中正确的是( )
A.①② B.②③ C.①②③ D.①③
二、填空题(每小题4分,共20分)
11.如图,直线a,b垂直相交于点O,曲线C是中心对称图形,点O为其对称中心,点A的对称点是点,于点B,于点D.若,,则阴影部分的面积之和为___________.
12.如图,在中,,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点,若,面积为12,则长度的最小值为______.
13.如图,点P为内任一点,E,F分别为点P关于直线OA,OB对称的点.若,则____________°.
14.如图,在中,点D为边的中点,过点D作,连接并延长交边于点F,连接并延长交边于点E,,,则的值为__________.
15.如图,四边形ABCD的对角线AC,BD相交于点O,.下列结论:
①;
②;
③;
④;
⑤四边形ABCD是轴对称图形.其中所有正确结论的序号是________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在四边形ABCD中,
(1)画出四边形,使四边形与四边形ABCD关于直线MN成轴对称;
(2)画出四边形,使四边形与四边形ABCD关于点O中心对称;
(3)四边形与四边形是否对称,若对称请在图中画出对称轴或对称中心.
17.(8分)如图,在中,,点M,N分别在边AB,BC上,连接AN,且和关于直线MN对称.
(1)若,则的度数为______.
(2)若,,且的周长为36,求的周长.
18.(10分)如图,,点M,N分别是边,上的定点,点P,Q分别是边、上的动点.
(1)画图说明,当最小时,找出P和Q的位置.
(2)记,,当最小时,求的值.
19.(10分)(1)如图①,O为AB的中点,直线、分别经过点O、B,且,以点O为圆心,OA长为半径画弧交直线于点C,连接AC.求证:直线垂直平分AC;
(2)如图②,平面内直线,且相邻两直线间距离相等,点P、Q分别在直线、上,连接PQ.用圆规和无刻度的直尺在直线上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)
20.(12分)教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,的周长是12,BO,CO分别平分和,于点D,若,则的面积为________.
21.(12分)如图,
(1)【情景呈现】画,并画的平分线OC.把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与的两边OA,OB相交于点E,F,若,(如图1),则;若把三角尺绕点P旋转(如图2),则_________.(选填“<”,“>”或“=”)(不用证明)
(2)【理解应用】在(1)的条件下,过点P作直线,分别交OA,OB于点G,H,如图3.
①图中全等三角形共有_________对;(不添加辅助线)
②直接写出与之间的数量关系为_________.
(3)【拓展延伸】如图4,画,并画的平分线OC,在OC上任取一点P,作,当时,的两边分别与OA,OB相交于点E,F,PE与PF相等吗?请说明理由.
答案以及解析
1.答案:D
解析:A、是轴对称图形,不是中心对称图形,故A选项不合题意;
B、是轴对称图形,不是中心对称图形,故B选项不符合题意;
C、不是轴对称图形,是中心对称图形,故C选项不合题意;
D、既是轴对称图形,又是中心对称图形,故D选项合题意.
故选:D.
2.答案:C
解析:点P到点A、点B的距离相等,
点P在线段的垂直平分线上,
故选:C.
3.答案:B
解析:与关于直线MN对称,,,,故选项A,C,D正确.
4.答案:A
解析:由题意得AG是的角平分线,如图,过点G作于点H.,,的面积.故选A.
5.答案:B
解析:与关于点O成中心对称,,,点A的对称点是点,,故A,C,D正确.
6.答案:D
解析:,又,①正确;,又,,②正确;,,又,点D在的平分线上,③正确.故选D.
7.答案:A
解析:直线m是中BC边的垂直平分线,
,
周长,
两点之间线段最短,
,
的周长,
,,
周长最小为,
故选:A.
8.答案:C
解析:过点O作于D,于E,于F,
点O是内心,
,
,
故选:C.
9.答案:A
解析:如图,过点D作于点G,
AD是的角平分线,,,
,
,
F是BC中点,
.
故选:A.
10.答案:B
解析:和的平分线AE、BF相交于点O,
,,
,故①错误;
,
,
,
,
,
如图,在AB上取一点H,使,
BF是的角平分线,
,
,
,
,
,
,
,,
,
,
,故②正确;
作于G,于M,如图所示:
和的平分线AE、BF相交于点O,
点O在的平分线上,
,
,故③正确;
故选:B.
11.答案:6
解析:过点A作于点E,曲线C是中心对称图形,点A的对称点是点,,,阴影部分的面积之和等于四边形ABOE的面积,,,,阴影部分的面积之和为.
12.答案:6
解析:如图,连接AD,AM,
因为,D为BC的中点,
所以
因为,
所以,
因为EF垂直平分线段AB,
所以,
所以,
所以的最小值为6,
故答案为:6.
13.答案:150
解析:如图,连接OP,E,F分别为点P关于直线OA,OB对称的点,,,,,,,又,,.
14.答案:
解析:作于点M,于点N,
点D为边的中点,,
,
,
,,且,
,
,,,
,
,
,
,
在和中,,
,
,,
,
,,
,
,且,,
,
,
,
故答案为:.
15.答案:①②③⑤
解析:,
,,,,
,故①正确;
四边形ABCD的对角线AC,BD相交于点O,
,
在和中,
,
,故③正确;
,故②正确.
,,
四边形ABCD是轴对称图形,故⑤正确.
故答案为:①②③⑤.
16.答案:(1)图见解析;
(2)图见解析;
(3)图见解析;
解析:(1)四边形如图所示;
(2)四边形如图所示;
(3)如图所示,四边形与四边形关于直线PQ成轴对称.
17.答案:(1)
(2)21
解析:(1),,
,
和关于直线MN对称,
,
,
故答案为:.
(2)的周长为36,
,
,,
,解得,
.
和关于直线MN对称,
,
的周长.
18.答案:(1)见解析
(2)
解析:(1)如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,如图所示:
(2)由(1)知M关于的对称点,N关于的对称点,
,,
,
,
.
19.答案:(1)解:如图①,连接OC,
,,
直线平分AC,
由作图可知:,
,
垂直AC,
,
垂直AC,
即直线垂直平分AC.
(2)如图②,以与PQ的交点O为圆心,OP长为半径画弧交直线于点C,连接PC并延长交直线于点D,此时线段PD最短,点D即为所求.
解析:
20.答案:定理证明:见解析,定理应用:18
解析:定理证明:是的角平分线,
,
,,
,
在和中,
,
,
;
定理应用:过O作与E,于F,
,CO分别平分和,
,,
,
,
的周长是12,
,
的面积:,
故答案为:18.
21.答案:(1)=
(2)①3②
(3),理由见解析
解析:(1)如图,过点P作,,垂足是M,N,
,
,
OC是的平分线,
,
,
,
,
在和中,
,
,
.
故答案为:=;
(2)①OC平分,
,
,
,
,
,
,
在和中,
,
,
同理可证明,
,
,
全等三角形有3对;
②,,
,
,,
.
故答案为:①3;②;
(3)如图,作于G,于H,
,,
,
OC平分,
,
,,且,
又,
,
,
,
在和中,
,
,
.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
